Skip to main content
SpringerLink
Log in

Uncertainty-guided joint unbalanced optimal transport for unsupervised domain adaptation

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

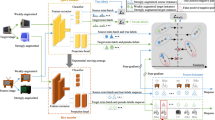
Unsupervised domain adaptation aims to improve the performance of model generalization on unlabeled target domain by utilizing given labeled training samples from source domain. The optimal transport theory has been widely used to reduce domain discrepancy. However, most existing optimal transport-based approaches inevitably have the pair-wise mismatching problem during alignment of feature distributions. Besides, most current studies tend to focus on the improvement of prediction accuracy while ignoring the uncertainty estimation of noisy training samples, which is particularly important for the learning of transferrable model. To alleviate these issues, we propose a framework, Uncertainty-guided Joint Unbalanced Optimal Transport (UJUOT), which employs a feature uncertainty estimation (FUE) mechanism and an unbalanced optimal transport strategy. FUE encodes uncertainty by modeling each image embedding as a Gaussian distribution, improving representation space with better inter-class separability and intra-class compactness. It not only makes it easier for the domain alignment, but also lets the model more robust to noisy data. In addition, to reduce negative transfer, we design a novel unbalanced optimal transport (UOT) strategy to achieve precise pair-wise matching, which fully utilizes discriminative class-aware information to learn mass adaptively in order to determine best transport plan. To our best knowledge, this is a pioneering work of introducing data uncertainty to unsupervised domain adaptation. Extensive experiments on various standard datasets prove that our proposal can significantly improve transfer performance, outperforming state-of-the-art methods in many aspects.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availability

The experimental datasets are open source and can be obtained through references.

References

  1. Li M, Zhai Y-M, Luo Y-W, Ge P-F, Ren C-X Enhanced transport distance for unsupervised domain adaptation In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp 13936–13944 (2020)

  2. Lee C-Y, Batra T, Baig MH, Ulbricht D Sliced wasserstein discrepancy for unsupervised domain adaptation. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp 10285–10295 (2019)

  3. Tzeng E, Hoffman J, Zhang N, Saenko K, Darrell T Deep domain confusion: maximizing for domain invariance. arXiv preprint arXiv:1412.3474 (2014)

  4. Sun B, Saenko K Deep coral: Correlation alignment for deep domain adaptation. In: European Conference on Computer Vision, pp. 443–450 (2016) Springer

  5. Zhuang F, Cheng X, Luo P, Pan SJ, He Q (2015) Supervised representation learning: transfer learning with deep autoencoders. In: Twenty-Fourth International Joint Conference on Artificial Intelligence

  6. Ganin Y, Ustinova E, Ajakan H, Germain P, Larochelle H, Laviolette F, Marchand M, Lempitsky V (2016) Domain-adversarial training of neural networks. J Mach Learn Res 17(1):2030–2096

    MathSciNet  MATH  Google Scholar 

  7. Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y (2014) Generative adversarial nets. arXiv:1406.2661 (preprint)

  8. Hoffman J, Tzeng E, Park T, Zhu J-Y, Isola P, Saenko K, Efros A, Darrell T (2018) Cycada: Cycle-consistent adversarial domain adaptation. In: International Conference on Machine Learning, PMLR pp 1989–1998

  9. Courty N, Flamary R, Tuia D (2014) Domain adaptation with regularized optimal transport. In: Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Springer pp 274–289

  10. Yan Y, Li W, Wu H, Min H, Tan M, Wu Q (2018) Semi-supervised optimal transport for heterogeneous domain adaptation. IJCAI 7:2969–2975

    Google Scholar 

  11. Courty N, Flamary R, Habrard A, Rakotomamonjy A (2017) Joint distribution optimal transportation for domain adaptation. arXiv preprint arXiv:1705.08848

  12. Courty N, Flamary R, Tuia D, Rakotomamonjy A (2016) Optimal transport for domain adaptation. IEEE Trans Pattern Anal Mach Intell 39(9):1853–1865

    Article  Google Scholar 

  13. Pan SJ, Yang Q (2009) A survey on transfer learning. IEEE Trans Knowl Data Eng 22(10):1345–1359

    Article  Google Scholar 

  14. Ben-David S, Blitzer J, Crammer K, Pereira F et al (2007) Analysis of representations for domain adaptation. Adv Neural Inf Process Syst 19:137

    Google Scholar 

  15. Chen Z, Chen C, Jin X, Liu Y, Cheng Z (2020) Deep joint two-stream wasserstein auto-encoder and selective attention alignment for unsupervised domain adaptation. Neural Comput Appl 32(11):7489–7502

    Article  Google Scholar 

  16. Cheng Z, Chen C, Chen Z, Fang K, Jin X (2021) Robust and high-order correlation alignment for unsupervised domain adaptation. Neural Comput Appl 33(12):6891–6903

    Article  Google Scholar 

  17. Long M, Zhu H, Wang J, Jordan MI (2017) Deep transfer learning with joint adaptation networks. In: International Conference on Machine Learning, PMLR pp 2208–2217

  18. Long M, Cao Y, Wang J, Jordan M (2015) Learning transferable features with deep adaptation networks. In: International Conference on Machine Learning, pp 97–105 PMLR

  19. Kang G, Jiang L, Yang Y, Hauptmann AG (2019) Contrastive adaptation network for unsupervised domain adaptation. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp 4893–4902

  20. Pan Y, Yao T, Li Y, Wang Y, Ngo C-W, Mei T (2019) Transferrable prototypical networks for unsupervised domain adaptation. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp 2239–2247

  21. Snell J, Swersky K, Zemel RS (2017) Prototypical networks for few-shot learning. arXiv preprint arXiv:1703.05175

  22. Wang J, Feng W, Chen Y, Yu H, Huang M, Yu PS (2018) Visual domain adaptation with manifold embedded distribution alignment. In: Proceedings of the 26th ACM International Conference on Multimedia, pp 402–410

  23. Wang J, Chen Y, Feng W, Yu H, Huang M, Yang Q (2020) Transfer learning with dynamic distribution adaptation. ACM Transactions Intell Syst Technol (TIST) 11(1):1–25

    Google Scholar 

  24. Tzeng E, Hoffman J, Saenko K, Darrell T (2017) Adversarial discriminative domain adaptation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 7167–7176

  25. Bousmalis K, Silberman N, Dohan D, Erhan D, Krishnan D (2017) Unsupervised pixel-level domain adaptation with generative adversarial networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 3722–3731

  26. Sankaranarayanan S, Balaji Y, Castillo CD, Chellappa R (2018) Generate to adapt: aligning domains using generative adversarial networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 8503–8512

  27. Murez Z, Kolouri S, Kriegman D, Ramamoorthi R, Kim K (2018) Image to image translation for domain adaptation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 4500–4509

  28. Zhang H, Cisse M, Dauphin YN, Lopez-Paz D (2017) mixup: beyond empirical risk minimization. arXiv preprint arXiv:1710.09412

  29. Wu Y, Inkpen D, El-Roby A (2020) Dual mixup regularized learning for adversarial domain adaptation. In: European Conference on Computer Vision, Springer pp 540–555

  30. Monge G Mémoire sur la théorie des déblais et des remblais. Histoire de l’Académie Royale des Sciences de Paris (1781)

  31. Villani C (2009) Optimal transport: old and new. Springer, New York

    Book  MATH  Google Scholar 

  32. Perrot M, Courty N, Flamary R, Habrard A (2016) Mapping estimation for discrete optimal transport. Adv Neural Inf Process Syst 29:4197–4205

    Google Scholar 

  33. Damodaran BB, Kellenberger B, Flamary R, Tuia D, Courty N (2018) Deepjdot: deep joint distribution optimal transport for unsupervised domain adaptation. In: Proceedings of the European Conference on Computer Vision (ECCV), pp 447–463

  34. Xu R, Liu P, Wang L, Chen C, Wang J (2020) Reliable weighted optimal transport for unsupervised domain adaptation. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp 4394–4403

  35. Fatras K, Séjourné T, Flamary R, Courty N (2021) Unbalanced minibatch optimal transport; applications to domain adaptation. In: International Conference on Machine Learning, pp 3186–3197 PMLR

  36. Gal Y, Ghahramani Z (2016) Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In: International Conference on Machine Learning, pp 1050–1059 PMLR

  37. Kendall A, Gal Y (2017) What uncertainties do we need in bayesian deep learning for computer vision? arXiv preprint arXiv:1703.04977

  38. Chang J, Lan Z, Cheng C, Wei Y (2020) Data uncertainty learning in face recognition. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp 5710–5719

  39. Yu T, Li D, Yang Y, Hospedales TM, Xiang T (2019) Robust person re-identification by modelling feature uncertainty. In: Proceedings of the IEEE/CVF International Conference on Computer Vision, pp 552–561

  40. Isobe S, Arai S (2017) Deep convolutional encoder-decoder network with model uncertainty for semantic segmentation. In: 2017 IEEE International Conference on INnovations in Intelligent SysTems and Applications (INISTA), pp 365–370 IEEE

  41. Lee J, Lee G (2020) Model uncertainty for unsupervised domain adaptation. In: 2020 IEEE International Conference on Image Processing (ICIP), pp 1841–1845 IEEE

  42. Chen C, Chen Z, Jiang B, Jin X (2019) Joint domain alignment and discriminative feature learning for unsupervised deep domain adaptation. In: Proceedings of the AAAI Conference on Artificial Intelligence, vol 33, pp 3296–3303

  43. Angenent S, Haker S, Tannenbaum A (2003) Minimizing flows for the Monge-Kantorovich problem. SIAM J Math Anal 35(1):61–97

    Article  MathSciNet  MATH  Google Scholar 

  44. Dieci L, Walsh JD III (2019) The boundary method for semi-discrete optimal transport partitions and wasserstein distance computation. J Comput Appl Math 353:318–344

    Article  MathSciNet  MATH  Google Scholar 

  45. Zhan F, Yu Y, Cui K, Zhang G, Lu S, Pan J, Zhang C, Ma F, Xie X, Miao C (2021) Unbalanced feature transport for exemplar-based image translation. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp 15028–15038

  46. Chizat L, Peyré G, Schmitzer B, Vialard F-X (2018) Scaling algorithms for unbalanced optimal transport problems. Math Comput 87(314):2563–2609

    Article  MathSciNet  MATH  Google Scholar 

  47. Lu W, Chen Y, Wang J, Qin X (2021) Cross-domain activity recognition via substructural optimal transport. Neurocomputing 454:65–75

    Article  Google Scholar 

  48. Bhatia R, Jain T, Lim Y (2019) On the bures-wasserstein distance between positive definite matrices. Expo Math 37(2):165–191

    Article  MathSciNet  MATH  Google Scholar 

  49. Chapelle O, Zien A (2005) Semi-supervised classification by low density separation. In: International Workshop on Artificial Intelligence and Statistics, pp 57–64 PMLR

  50. Pham K, Le K, Ho N, Pham T, Bui H (2020) On unbalanced optimal transport: an analysis of sinkhorn algorithm. In: International Conference on Machine Learning, pp 7673–7682 PMLR

  51. Cuturi M (2013) Sinkhorn distances: lightspeed computation of optimal transport. Adv Neural Inf Process Syst 26:2292–2300

    Google Scholar 

  52. Netzer Y, Wang T, Coates A, Bissacco A, Wu B, Ng AY (2011) Reading digits in natural images with unsupervised feature learning

  53. Hull JJ (1994) A database for handwritten text recognition research. IEEE Trans Pattern Anal Mach Intell 16(5):550–554

    Article  Google Scholar 

  54. LeCun Y, Bottou L, Bengio Y, Haffner P (1998) Gradient-based learning applied to document recognition. Proc IEEE 86(11):2278–2324

    Article  Google Scholar 

  55. Saenko K, Kulis B, Fritz M, Darrell T (2010) Adapting visual category models to new domains. In: European Conference on Computer Vision, Springer pp 213–226

  56. Venkateswara H, Eusebio J, Chakraborty S, Panchanathan S (2017) Deep hashing network for unsupervised domain adaptation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 5018–5027

  57. Peng X, Usman B, Kaushik N, Wang D, Hoffman J, Saenko K (2018) Visda: a synthetic-to-real benchmark for visual domain adaptation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, pp 2021–2026

  58. Saito K, Watanabe K, Ushiku Y, Harada T (2018) Maximum classifier discrepancy for unsupervised domain adaptation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 3723–3732 (2018)

  59. Chen X, Wang S, Long M, Wang J (2019) Transferability vs. discriminability: batch spectral penalization for adversarial domain adaptation. In: International Conference on Machine Learning, pp 1081–1090 PMLR

  60. He K, Zhang X, Ren S, Sun J (2016) Deep residual learning for image recognition In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp 770–778

  61. van der Maaten L, Hinton G (2008) Visualizing data using t-sne. J Mach Learn Res 9(11)

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No.61975048).

Author information

Authors and Affiliations

  1. College of Information Science & Electronic Engineering, Zhejiang University, Hangzhou, 310027, Zhejiang, China

    Jun Dan, Tao Jin, Shunjie Dong & Yixuan Shen

  2. School of Communication Engineering, Hangzhou Dianzi University, Hangzhou, 310018, Zhejiang, China

    Hao Chi

Authors
  1. Jun Dan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tao Jin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hao Chi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shunjie Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yixuan Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tao Jin.

Ethics declarations

Conflicts of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dan, J., Jin, T., Chi, H. et al. Uncertainty-guided joint unbalanced optimal transport for unsupervised domain adaptation. Neural Comput & Applic 35, 5351–5367 (2023). https://doi.org/10.1007/s00521-022-07976-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-07976-x

Keywords

Search

Navigation