Skip to main content
SpringerLink
Log in

Hybrid binary COOT algorithm with simulated annealing for feature selection in high-dimensional microarray data

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

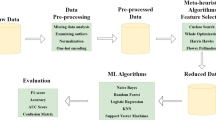
Abstract

Microarray analysis of gene expression can help with disease and cancer diagnosis and prognosis. Identification of gene biomarkers is one of the most difficult issues in microarray cancer classification due to the diverse complexity of different cancers and the high dimensionality of data. In this paper, a new gene selection strategy based on the binary COOT (BCOOT) optimization algorithm is proposed. The COOT algorithm is a newly proposed optimizer whose ability to solve gene selection problems has yet to be explored. Three binary variants of the COOT algorithm are suggested to search for the targeting genes to classify cancer and diseases. The proposed algorithms are BCOOT, BCOOT-C, and BCOOT-CSA. In the first method, a hyperbolic tangent transfer function is used to convert the continuous version of the COOT algorithm to binary. In the second approach, a crossover operator (C) is used to improve the global search of the BCOOT algorithm. In the third method, BCOOT-C is hybridized with simulated annealing (SA) to boost the algorithm’s local exploitation capabilities in order to find robust and stable informative genes. Furthermore, minimum redundancy maximum relevance (mRMR) is used as a prefiltering technique to eliminate redundant genes. The proposed algorithms are tested on ten well-known microarray datasets and then compared to other powerful optimization algorithms, and recent state-of-the-art gene selection techniques. The experimental results demonstrate that the BCOOT-CSA approach surpasses BCOOT and BCOOT-C and outperforms other techniques in terms of prediction accuracy and the number of selected genes in most cases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Dashtban M, Balafar M (2017) Gene selection for microarray cancer classification using a new evolutionary method employing artificial intelligence concepts. Genomics 109:91–107. https://doi.org/10.1016/j.ygeno.2017.01.004

    Article  Google Scholar 

  2. Pashaei E, Pashaei E (2021) Gene selection using hybrid dragonfly black hole algorithm: a case study on RNA-seq COVID-19 data. Anal Biochem 627:114242. https://doi.org/10.1016/j.ab.2021.114242

    Article  Google Scholar 

  3. Zhang G, Hou J, Wang J et al (2020) Feature selection for microarray data classification using hybrid information gain and a modified binary krill herd algorithm. Interdiscip Sci Comput Life Sci 12:288–301. https://doi.org/10.1007/s12539-020-00372-w

    Article  Google Scholar 

  4. Alomari OA, Khader AT, Al-Betar MA, Awadallah MA (2018) A novel gene selection method using modified MRMR and hybrid bat-inspired algorithm with β-hill climbing. Appl Intell 48:4429–4447. https://doi.org/10.1007/s10489-018-1207-1

    Article  Google Scholar 

  5. Alomari OA, Makhadmeh SN, Al-Betar MA et al (2021) Gene selection for microarray data classification based on Gray Wolf Optimizer enhanced with TRIZ-inspired operators. Knowl-Based Syst 223:107034. https://doi.org/10.1016/J.KNOSYS.2021.107034

    Article  Google Scholar 

  6. Gao L, Ye M, Lu X, Huang D (2017) Hybrid method based on information gain and support vector machine for gene selection in cancer classification. Genomics Proteomics Bioinforma 15:389–395. https://doi.org/10.1016/j.gpb.2017.08.002

    Article  Google Scholar 

  7. Dabba A, Tari A, Meftali S, Mokhtari R (2021) Gene selection and classification of microarray data method based on mutual information and moth flame algorithm. Expert Syst Appl 166:114012. https://doi.org/10.1016/J.ESWA.2020.114012

    Article  Google Scholar 

  8. Shreem SS, Ahmad Nazri MZ, Abdullah S, Sani NS (2022) Hybrid symmetrical uncertainty and reference set harmony search algorithm for gene selection problem. Mathematics 10:374. https://doi.org/10.3390/MATH10030374

    Article  Google Scholar 

  9. Jain I, Jain VK, Jain R (2018) Correlation feature selection based improved-Binary Particle Swarm Optimization for gene selection and cancer classification. Appl Soft Comput J 62:203–215. https://doi.org/10.1016/j.asoc.2017.09.038

    Article  Google Scholar 

  10. Pashaei E, Aydin N (2018) Markovian encoding models in human splice site recognition using SVM. Comput Biol Chem 73:159–170. https://doi.org/10.1016/j.compbiolchem.2018.02.005

    Article  Google Scholar 

  11. Pashaei E, Yilmaz A, Aydin N (2016) A combined SVM and Markov model approach for splice site identification. In: 6th International conference on computer and knowledge engineering (ICCKE 2016). IEEE, pp. 200–204

  12. Ahmed MS, Shahjaman M, Rana MM, Mollah MNH (2017) Robustification of Naïve Bayes classifier and its application for microarray gene expression data analysis. Biomed Res Int 2017:3020627. https://doi.org/10.1155/2017/3020627

    Article  Google Scholar 

  13. Pashaei E, Pashaei E (2021) Training feedforward neural network using enhanced black hole algorithm: a case study on COVID-19 related ACE2 gene expression classification. Arab J Sci Eng 46:3807–3828. https://doi.org/10.1007/s13369-020-05217-8

    Article  Google Scholar 

  14. Al-Betar MA, Alomari OA, Abu-Romman SM (2020) A TRIZ-inspired bat algorithm for gene selection in cancer classification. Genomics 112:114–126. https://doi.org/10.1016/j.ygeno.2019.09.015

    Article  Google Scholar 

  15. Pashaei E, Ozen M, Aydin N (2016) Biomarker discovery based on BBHA and AdaboostM1 on microarray data for cancer classification. In: 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS). IEEE, pp 3080–3083

  16. Mafarja M, Mirjalili S (2017) Hybrid Whale Optimization Algorithm with simulated annealing for feature selection. Neurocomputing 260:302–312. https://doi.org/10.1016/j.neucom.2017.04.053

    Article  Google Scholar 

  17. Abdel-Basset M, Ding W, El-Shahat D (2021) A hybrid Harris Hawks optimization algorithm with simulated annealing for feature selection. Artif Intell Rev 54:593–637. https://doi.org/10.1007/s10462-020-09860-3

    Article  Google Scholar 

  18. Khamees M, Albakry A, Shaker K (2018) Multi-objective feature selection: hybrid of Salp Swarm and simulated annealing approach. In: Al-mamory SO, Alwan JK, Hussein AD (eds) New trends in information and communications technology applications. NTICT 2018. Communications in computer and information science. Springer, Berlin, pp 129–142

    Google Scholar 

  19. Chantar H, Tubishat M, Essgaer M, Mirjalili S (2021) Hybrid binary dragonfly algorithm with simulated annealing for feature selection. SN Comput Sci 2:295. https://doi.org/10.1007/s42979-021-00687-5

    Article  Google Scholar 

  20. Shukla AK, Singh P, Vardhan M (2020) An adaptive inertia weight teaching-learning-based optimization algorithm and its applications. Appl Math Model 77:309–326. https://doi.org/10.1016/j.apm.2019.07.046

    Article  MathSciNet  MATH  Google Scholar 

  21. Shukla AK, Singh P, Vardhan M (2019) A new hybrid wrapper TLBO and SA with SVM approach for gene expression data. Inf Sci (Ny) 503:238–254. https://doi.org/10.1016/j.ins.2019.06.063

    Article  MathSciNet  Google Scholar 

  22. Pandey AC, Rajpoot DS (2019) Feature selection method based on grey wolf optimization and simulated annealing. Recent Adv Comput Sci Commun 14:635–646. https://doi.org/10.2174/2213275912666190408111828

    Article  Google Scholar 

  23. Tran B, Xue B, Zhang M (2019) Variable-length particle swarm optimization for feature selection on high-dimensional classification. IEEE Trans Evol Comput 23:473–487. https://doi.org/10.1109/TEVC.2018.2869405

    Article  Google Scholar 

  24. Yan C, Ma J, Luo H, Patel A (2019) Hybrid binary coral reefs optimization algorithm with simulated annealing for feature selection in high-dimensional biomedical datasets. Chemom Intell Lab Syst 184:102–111. https://doi.org/10.1016/j.chemolab.2018.11.010

    Article  Google Scholar 

  25. Yan C, Ma J, Luo H et al (2019) A novel feature selection method for high-dimensional biomedical data based on an improved binary clonal flower pollination algorithm. Hum Hered 84:34–46. https://doi.org/10.1159/000501652

    Article  Google Scholar 

  26. Bir-Jmel A, Douiri SM, Elbernoussi S (2019) Gene selection via a new hybrid ant colony optimization algorithm for cancer classification in high-dimensional data. Comput Math Methods Med 2019:1–20. https://doi.org/10.1155/2019/7828590

    Article  MATH  Google Scholar 

  27. Pashaei E, Pashaei E (2022) An efficient binary chimp optimization algorithm for feature selection in biomedical data classification. Neural Comput Appl 34:6427–6451. https://doi.org/10.1007/S00521-021-06775-0/TABLES/12

    Article  Google Scholar 

  28. Ewees AA, Al-qaness MAA, Abualigah L et al (2021) Boosting arithmetic optimization algorithm with genetic algorithm operators for feature selection: case study on cox proportional hazards model. Mathematics 9:2321. https://doi.org/10.3390/MATH9182321

    Article  Google Scholar 

  29. Dash R (2021) An adaptive harmony search approach for gene selection and classification of high dimensional medical data. J King Saud Univ Comput Inf Sci 33:195–207. https://doi.org/10.1016/j.jksuci.2018.02.013

    Article  Google Scholar 

  30. Luo J, Zhou D, Jiang L, Ma H (2022) A particle swarm optimization based multiobjective memetic algorithm for high-dimensional feature selection. Memetic Comput 14:77–93. https://doi.org/10.1007/S12293-022-00354-Z/TABLES/6

    Article  Google Scholar 

  31. Agarwalla P, Mukhopadhyay S (2022) GENEmops: supervised feature selection from high dimensional biomedical dataset. Appl Soft Comput 123:108963. https://doi.org/10.1016/J.ASOC.2022.108963

    Article  Google Scholar 

  32. Chaudhuri A, Sahu TP (2021) A hybrid feature selection method based on Binary Jaya algorithm for micro-array data classification. Comput Electr Eng 90:106963. https://doi.org/10.1016/j.compeleceng.2020.106963

    Article  Google Scholar 

  33. Zhou Y, Zhang W, Kang J et al (2021) A problem-specific non-dominated sorting genetic algorithm for supervised feature selection. Inf Sci (NY) 547:841–859. https://doi.org/10.1016/j.ins.2020.08.083

    Article  MathSciNet  MATH  Google Scholar 

  34. Naruei I, Keynia F (2021) A new optimization method based on COOT bird natural life model. Expert Syst Appl 183:115352. https://doi.org/10.1016/J.ESWA.2021.115352

    Article  Google Scholar 

  35. Houssein EH, Hashim FA, Ferahtia S, Rezk H (2022) Battery parameter identification strategy based on modified coot optimization algorithm. J Energy Storage 46:103848. https://doi.org/10.1016/J.EST.2021.103848

    Article  Google Scholar 

  36. Mostafa RR, Hussien AG, Khan MA, et al (2022) Enhanced COOT optimization algorithm for Dimensionality Reduction. In: Fifth International conference of women in data science at prince Sultan University (WiDS PSU). IEEE, pp 43–48

  37. Alqahtani AS, Saravanan P, Maheswari M, Alshmrany S (2022) An automatic query expansion based on hybrid CMO-COOT algorithm for optimized information retrieval. J Supercomput 78:8625–8643. https://doi.org/10.1007/S11227-021-04171-Y/TABLES/13

    Article  Google Scholar 

  38. Memarzadeh G, Keynia F (2021) A new optimal energy storage system model for wind power producers based on long short term memory and Coot Bird Search Algorithm. J Energy Storage 44:103401. https://doi.org/10.1016/J.EST.2021.103401

    Article  Google Scholar 

  39. Mahdy A, Hasanien HM, Helmy W et al (2022) Transient stability improvement of wave energy conversion systems connected to power grid using anti-windup-coot optimization strategy. Energy 245:123321. https://doi.org/10.1016/J.ENERGY.2022.123321

    Article  Google Scholar 

  40. Kien LC, Bich Nga TT, Phan TM, Nguyen TT (2022) Coot optimization algorithm for optimal placement of photovoltaic generators in distribution systems considering variation of load and solar radiation. Math Probl Eng 2022:1–17. https://doi.org/10.1155/2022/2206570

    Article  Google Scholar 

  41. Hussien AM, Turky RA, Alkuhayli A et al (2022) Coot bird algorithms-based tuning PI controller for optimal microgrid autonomous operation. IEEE Access 10:6442–6458. https://doi.org/10.1109/ACCESS.2022.3142742

    Article  Google Scholar 

  42. Huang Y, Zhang J, Wei W et al (2022) Research on coverage optimization in a WSN based on an improved COOT bird algorithm. Sensors 22:3383. https://doi.org/10.3390/S22093383

    Article  Google Scholar 

  43. Faris H, Mafarja MM, Heidari AA et al (2018) An efficient binary Salp Swarm Algorithm with crossover scheme for feature selection problems. Knowl-Based Syst 154:43–67. https://doi.org/10.1016/J.KNOSYS.2018.05.009

    Article  Google Scholar 

  44. Xue Y, Zhu H, Liang J, Słowik A (2021) Adaptive crossover operator based multi-objective binary genetic algorithm for feature selection in classification. Knowl-Based Syst 227:107218. https://doi.org/10.1016/J.KNOSYS.2021.107218

    Article  Google Scholar 

  45. Awadallah MA, Hammouri AI, Al-Betar MA et al (2022) Binary Horse herd optimization algorithm with crossover operators for feature selection. Comput Biol Med 141:105152. https://doi.org/10.1016/J.COMPBIOMED.2021.105152

    Article  Google Scholar 

  46. Pashaei E, Pashaei E (2019) Gene Selection using Intelligent Dynamic Genetic Algorithm and Random Forest. In: 11th International Conference on Electrical and Electronics Engineering (ELECO). IEEE, pp 470–474

  47. Dabba A, Tari A, Meftali S (2021) Hybridization of Moth flame optimization algorithm and quantum computing for gene selection in microarray data. J Ambient Intell Humaniz Comput 12:2731–2750. https://doi.org/10.1007/s12652-020-02434-9

    Article  Google Scholar 

  48. Bommert A, Sun X, Bischl B et al (2020) Benchmark for filter methods for feature selection in high-dimensional classification data. Comput Stat Data Anal 143:1–19. https://doi.org/10.1016/j.csda.2019.106839

    Article  MathSciNet  MATH  Google Scholar 

  49. Lin J, Bai J, Reutskiy S, Lu J (2022) A novel RBF-based meshless method for solving time-fractional transport equations in 2D and 3D arbitrary domains. Eng Comput 1:1–18. https://doi.org/10.1007/S00366-022-01601-0/FIGURES/12

    Article  Google Scholar 

  50. Lin J, Feng W, Reutskiy S et al (2021) A new semi-analytical method for solving a class of time fractional partial differential equations with variable coefficients. Appl Math Lett 112:106712. https://doi.org/10.1016/J.AML.2020.106712

    Article  MathSciNet  MATH  Google Scholar 

  51. Gad AG, Karam •, Sallam M, et al (2022) An improved binary sparrow search algorithm for feature selection in data classification. Neural Comput Appl 2022:1–49. https://doi.org/10.1007/S00521-022-07203-7

    Article  Google Scholar 

  52. Hammouri AI, Mafarja M, Al-Betar MA et al (2020) An improved dragonfly algorithm for feature selection. Knowl-Based Syst 203:106131. https://doi.org/10.1016/j.knosys.2020.106131

    Article  Google Scholar 

  53. Mafarja M, Mirjalili S (2018) Whale optimization approaches for wrapper feature selection. Appl Soft Comput J 62:441–453. https://doi.org/10.1016/j.asoc.2017.11.006

    Article  Google Scholar 

  54. Pashaei E, Pashaei E, Aydin N (2019) Gene selection using hybrid binary black hole algorithm and modified binary particle swarm optimization. Genomics 111:669–686. https://doi.org/10.1016/j.ygeno.2018.04.004

    Article  Google Scholar 

  55. Pashaei E, Pashaei E (2020) Gene selection for cancer classification using a new hybrid of binary black hole algorithm. In: 28th IEEE conference on signal processing and communications applications (SIU2020). IEEE, pp 1–4

  56. Pashaei E, Ozen M, Aydin N (2016) Random forest in splice site prediction of human genome. In: Kyriacou E, Christofides S, Pattichis C (eds) XIV Mediterranean conference on medical and biological engineering and computing. IFMBE Proceedings, vol 57. Springer, Berlin, pp 518–523

    Chapter  Google Scholar 

  57. Beheshti Z (2021) UTF: Upgrade transfer function for binary meta-heuristic algorithms. Appl Soft Comput 106:107346. https://doi.org/10.1016/j.asoc.2021.107346

    Article  Google Scholar 

  58. Mirjalili S, Lewis A (2013) S-shaped versus V-shaped transfer functions for binary Particle Swarm Optimization. Swarm Evol Comput 9:1–14. https://doi.org/10.1016/j.swevo.2012.09.002

    Article  Google Scholar 

  59. Zhu Z, Ong YS, Dash M (2007) Markov blanket-embedded genetic algorithm for gene selection. Pattern Recognit 40:3236–3248. https://doi.org/10.1016/j.patcog.2007.02.007

    Article  MATH  Google Scholar 

  60. Ambroise C, McLachlan GJ (2002) Selection bias in gene extraction on the basis of microarray gene-expression data. Proc Natl Acad Sci 99:6562–6566. https://doi.org/10.1073/pnas.102102699

    Article  MATH  Google Scholar 

  61. Abualigah L, Diabat A, Mirjalili S et al (2021) The arithmetic optimization algorithm. Comput Methods Appl Mech Eng 376:113609. https://doi.org/10.1016/J.CMA.2020.113609

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Software Engineering, Istanbul Aydin University, Istanbul, Turkey

    Elnaz Pashaei

  2. Department of Computer Engineering, Istanbul Gelisim University, Istanbul, Turkey

    Elham Pashaei

Authors
  1. Elnaz Pashaei
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Elham Pashaei
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Elnaz Pashaei implemented the model, conducted the experiments, and analyzed the data. Elham Pashaei devised the idea, designed the study, performed the statistical analysis, and wrote the manuscript. Both authors contributed to manuscript revisions and approved the final version of the manuscript.

Corresponding author

Correspondence to Elham Pashaei.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pashaei, E., Pashaei, E. Hybrid binary COOT algorithm with simulated annealing for feature selection in high-dimensional microarray data. Neural Comput & Applic 35, 353–374 (2023). https://doi.org/10.1007/s00521-022-07780-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-07780-7

Keywords

Search

Navigation