Skip to main content
SpringerLink
Log in

SBOX-CGA: substitution box generator based on chaos and genetic algorithm

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

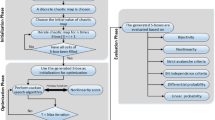
What makes artificial intelligence techniques so remarkable in the field of computer science is undoubtedly their success in producing effective solutions to difficult computational problems. In particular, metaheuristic optimization algorithms are a unique example of using artificial intelligence techniques to generate approximate solutions to problems that cannot be solved in polynomial time, called NP. Obtaining a substitution box (s-box) structure that will satisfy the desired requirements in cryptography is an example of these NP problems. In the literature, it is a hot topic to optimize the s-box structures obtained from chaotic entropy sources with heuristic algorithms to improve their cryptographic properties. The study with the highest nonlinearity value (110.25) based on optimization algorithms to date has been published in 2020. In this study, a method with a higher nonlinearity value than the algorithms previously proposed in the literature is developed. It has been shown that the nonlinearity value can be increased to 111.75. These results will be a basis for new research on the chaos-based s-box literature and will motivate new studies to develop alternative optimization algorithms in the future to obtain s-box structures based on the random selection equivalent to the AES s-box.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Artuğer F, Özkaynak F (2021) An effective method to improve nonlinearity value of substitution boxes based on random selection. Inf Sci 576:577–588

    Article  Google Scholar 

  2. Wei Y, Pasalic E, Zhang F, Hodžić S (2017) Efficient probabilistic algorithm for estimating the algebraic properties of Boolean functions for large n. Inf Sci 402:91–104

    Article  Google Scholar 

  3. Wu C, Feng D (2016) Boolean functions and their applications in cryptography. Springer, Berlin

    Book  Google Scholar 

  4. Daemen J, Rijmen V (1998) AES proposal: Rijndael. In: Proceedings of 1st advance encryption conference, CA, USA, pp 1–45

  5. Ors SB, Preneel B, Verbauwhede I (2007) Side-channel analysis attacks on hardware implementations of cryptographic algorithms, in Wireless Security and Cryptography-Specifications and Implementations. CRC Press, Boca Raton

    Google Scholar 

  6. Artuğer F, Özkaynak F (2022) A method for generation of substitution box based on random selection. Egypt. Inform. J. 23(1):127–135

    Article  Google Scholar 

  7. Nyberg K (1994) Differentially uniform mappings for cryptography. In: Proceedings of Eurocrypt. Lecture notes in computer science, vol 765. Springer, Berlin, pp 55–64

  8. Açikkapi MŞ, Özkaynak F (2021) A method to determine the most suitable initial conditions of chaotic map in statistical randomness applications. IEEE Access 9:1482–1494

    Article  Google Scholar 

  9. Chen G (2008) A novel heuristic method for obtaining S-boxes. Chaos Solitons Fractals 36(4):1028–1036

    Article  MathSciNet  Google Scholar 

  10. Hussain I, Shah T, Gondal MA, Khan WA, Mahmood H (2013) A group theoretic approach to construct cryptographically strong substitution boxes. Neural Comput Appl 23(1):97–104

    Article  Google Scholar 

  11. Farah T, Rhouma R, Belghith S (2017) A novel method for designing S-box based on chaotic map and teaching–learning-based optimization. Nonlinear Dyn 88(2):1059–1074

    Article  Google Scholar 

  12. Hematpour N, Ahadpour S (2021) Execution examination of chaotic S-box dependent on improved PSO algorithm. Neural Comput Appl 33(10):5111–5133

    Article  Google Scholar 

  13. Ahmad M, Bhatia D, Hassan Y (2015) A novel ant colony optimization based scheme for substitution box design. Procedia Comput Sci 57:572–580

    Article  Google Scholar 

  14. Alhadawi HS, Lambić D, Zolkipli MF, Ahmad M (2020) Globalized firefly algorithm and chaos for designing substitution box. J Inf Secur Appl 55:102671

    Google Scholar 

  15. Ahmed HA, Zolkipli MF, Ahmad M (2019) A novel efficient substitution-box design based on firefly algorithm and discrete chaotic map. Neural Comput Appl 31(11):7201–7210

    Article  Google Scholar 

  16. Tian Y, Lu Z (2017) Chaotic S-box: intertwining logistic map and bacterial foraging optimization. Math Problems Eng 2017:6969312

    Article  MathSciNet  Google Scholar 

  17. Wang Y, Wong KW, Li C, Li Y (2012) A novel method to design S-box based on chaotic map and genetic algorithm. Phys Lett A 376(6–7):827–833

    Article  Google Scholar 

  18. Alhadawi HS, Majid MA, Lambić D, Ahmad M (2021) A novel method of S-box design based on discrete chaotic maps and cuckoo search algorithm. Multimed Tools Appl 80(5):7333–7350

    Article  Google Scholar 

  19. Zamli KZ, Kader A, Din F, Alhadawi HS (2021) Selective chaotic maps Tiki-Taka algorithm for the S-box generation and optimization. Neural Comput Appl 33:16641–16658

    Article  Google Scholar 

  20. Zamli KZ (2021) Optimizing S-box generation based on the adaptive agent heroes and cowards algorithm. Expert Syst Appl 182:115305

    Article  Google Scholar 

  21. Wang Y, Zhang Z, Zhang LY, Feng J, Gao J, Lei P (2020) A genetic algorithm for constructing bijective substitution boxes with high nonlinearity. Inf Sci 523:152–166

    Article  MathSciNet  Google Scholar 

  22. Alatas B, Akin E, Ozer AB (2009) Chaos embedded particle swarm optimization algorithms. Chaos Solitons Fractals 40(4):1715–1734

    Article  MathSciNet  Google Scholar 

  23. Özkaynak F (2020) On the effect of chaotic system in performance characteristics of chaos based S-box designs. Phys. A Stat. Mech. Appl. 550:124072. https://doi.org/10.1016/j.physa.2019.124072

    Article  MATH  Google Scholar 

  24. Sprott J (2010) Elegant chaos algebraically simple chaotic flows. World Scientific, Singapore

    Book  Google Scholar 

  25. Artuğer F, Özkaynak F (2020) A novel method for performance improvement of chaos-based substitution boxes. Symmetry 12(4):571

    Article  Google Scholar 

  26. Alshammari BM, Guesmi R, Guesmi T, Alsaif H, Alzamil A (2021) Implementing a symmetric lightweight cryptosystem in highly constrained IoT devices by using a chaotic S-box. Symmetry 13(1):129

    Article  Google Scholar 

  27. Xian Y, Wang X (2021) Fractal sorting matrix and its application on chaotic image encryption. Inf Sci 547:1154–1169

    Article  MathSciNet  Google Scholar 

  28. Ibrahim S, Alhumyani H, Masud M, Alshamrani SS, Cheikhrouhou O, Muhammad G, Hossain MS, Abbas AM (2020) Framework for efficient medical image encryption using dynamic S-boxes and chaotic maps. IEEE Access 8:160433–160449. https://doi.org/10.1109/Access.628763910.1109/ACCESS.2020.3020746

    Article  Google Scholar 

Download references

Acknowledgements

Fatih Özkaynak was supported in part by the Scientific and Technological Research Council of Turkey under Grant 121E600.

Author information

Authors and Affiliations

  1. Department of Computer Engineering, Munzur University, 62200, Tunceli, Turkey

    Fırat Artuğer

  2. Department of Software Engineering, Fırat University, 23119, Elazig, Turkey

    Fatih Özkaynak

Authors
  1. Fırat Artuğer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fatih Özkaynak
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

FA was involved in the conceptualization, data curation, formal analysis, investigation, methodology and software. FÖ contributed to the supervision visualization, original draft, writing—review and editing, funding acquisition, project administration and resources.

Corresponding author

Correspondence to Fırat Artuğer.

Ethics declarations

Conflicts of interest

The authors declare that they have no conflicts of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Artuğer, F., Özkaynak, F. SBOX-CGA: substitution box generator based on chaos and genetic algorithm. Neural Comput & Applic 34, 20203–20211 (2022). https://doi.org/10.1007/s00521-022-07589-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-07589-4

Keywords

Search

Navigation