Skip to main content
SpringerLink
Log in

Exponential synchronization of memristor-based recurrent neural networks with multi-proportional delays

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

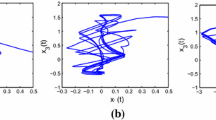
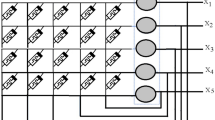
This paper focuses on the exponential synchronization of memristor-based recurrent neural networks with multi-proportional delays. Act as a vital mathematical model, the system with proportional delays has been widely popular in several scientific fields, such as biology, physics systems as well as control theory. In the sense of Filippov solutions, we receive a novel sufficient condition based on the theories of set-valued maps and differential inclusions, by constructing a proper Lyapunov functional and taking advantage of inequality techniques. Here, the condition is easy to be verified by algebraic methods. A couple of numerical examples and their simulations are given to illustrate the correctness and effectiveness of the obtained results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Chua L (1971) Memristor-the missing circuit element. IEEE Trans Circuit Theory 18(5):507–519

    Article  Google Scholar 

  2. Strukov D, Snider G, Stewart D, Williams R (2008) The missing memristor found. Nature 453(7191):80–83

    Article  Google Scholar 

  3. Zhang C, Shang J, Xue W, Tan H (2016) Convertible resistive switching characteristics between memory switching and threshold switching in a single ferritin-based memristor. Chem Commun 52(26):4828–4831

    Article  Google Scholar 

  4. Cho K, Lee S, Eshraghian K (2015) Memristor-CMOS logic and digital computational components. Microelectron J 46(3):214–220

    Article  Google Scholar 

  5. Sun Z, Chen X, Zhang Y, Li H, Chen Y (2012) Nonvolatile memories as the data storage system for implantable ECG recorder. ACM J Emerg Technol Comput Syst 8(2):1–16

    Article  Google Scholar 

  6. Jo S, Chang T, Ebong I, Bhadviya B (2010) Nanoscale memristor device as synapse in neuromorphic systems. Nano Lett 10(4):1297–1301

    Article  Google Scholar 

  7. Shin S, Kim K, Kang S (2011) Memristor applications for programmable analog ICs. IEEE Trans Nanotechnol 10(2):266–274

    Article  Google Scholar 

  8. Adhikari S, Yang C, Kim H, Chua L (2012) Memristor bridge synapse-based neural network and its learning. IEEE Trans Neural Netw Learn Syst 23(9):1426–1435

    Article  Google Scholar 

  9. Shen Y, Miao P, Huang Y, Shen Y (2015) Finite-time stability and its application for solving time-varying Sylvester equation by recurrent neural network. Neural Process Lett 42(3):763–784

    Article  Google Scholar 

  10. Stanimirovic P, Zivkovic I, Wei Y (2015) Recurrent neural network for computing the Drazin inverse. IEEE Trans Neural Netw Learn Syst 26(11):2830–2843

    Article  MathSciNet  Google Scholar 

  11. Qin S, Xue X (2015) A two-layer recurrent neural network for nonsmooth convex optimization problems. IEEE Trans Neural Netw Learn Syst 26(6):1149–1160

    Article  MathSciNet  Google Scholar 

  12. Wen S, Zeng Z, Huang T, Chen Y (2013) Passivity analysis of memristor-based recurrent neural networks with time-varying delays. J Frankl Inst 350(8):2354–2370

    Article  MathSciNet  MATH  Google Scholar 

  13. Wang H, Duan S, Li C, Wang L, Huang T (2017) Exponential stability analysis of delayed memristor-based recurrent neural networks with impulse effects. Neural Comput Appl 28(4):669–678

    Article  Google Scholar 

  14. Zhang G, Shen Y, Yin Q, Sun J (2015) Passivity analysis for memristor-based recurrent neural networks with discrete and distributed delays. Neural Netw 61(1):49–58

    Article  MATH  Google Scholar 

  15. Chandrasekar A, Rakkiyappan R, Li X (2016) Effects of bounded and unbounded leakage time-varying delays in memristor-based recurrent neural networks with different memductance functions. Neurocomputing 202(16):67–83

    Article  Google Scholar 

  16. Pecora L, Carroll T (1990) Synchronization in chaotic systems. Phys Rev Lett 64(8):821–824

    Article  MathSciNet  MATH  Google Scholar 

  17. Wang Q, Yu S, Li C, Lü J, Fang X (2016) Theoretical design and FPGA-based implementation of higher-dimensional digital chaotic systems. IEEE Trans Circuits I Regul Pap 63(3):401–412

    Article  MathSciNet  Google Scholar 

  18. Wen S, Zeng Z, Huang T, Meng Q, Yao W (2015) Lag synchronization of switched neural networks via neural activation function and applications in image encryption. IEEE Trans Neural Netw Learn Syst 26(7):1493–1502

    Article  MathSciNet  Google Scholar 

  19. Du W, Zhang J, Li Y, Qin S (2016) Synchronization between different networks with time-varying delay and its application in bilayer coupled public traffic network. Math Probl Eng 2016(2):1–11

    MathSciNet  MATH  Google Scholar 

  20. Garzagonzalez E, Posadascastillo C, Rodriguezlinan A, Hernandez C (2016) Chaotic synchronization of irregular complex network with hysteretic circuit-like oscillators in hamiltonian form and its application in private communications. Rev Mex Fis 62(1):51–59

    MathSciNet  Google Scholar 

  21. Wu X, Zhao X, Lü J, Tang L, Lu J (2016) Identifying topologies of complex dynamical networks with stochastic perturbations. IEEE Trans Control Netw Syst 3(4):379–389

    Article  MathSciNet  MATH  Google Scholar 

  22. Wang J, Feng J, Xu C, Chen Michael ZQ, Zhao Y, Feng J (2016) The synchronization of instantaneously coupled harmonic oscillators using sampled data with measurement noise. Automatica 66:155–162

    Article  MathSciNet  MATH  Google Scholar 

  23. Arenas A, Diaz-Guilera A, Kurths J, Moreno Y, Zhou C (2008) Synchronization in complex networks. Phys Rep 469(3):93–153

    Article  MathSciNet  Google Scholar 

  24. Liu H, Cao M, Wu C, Lu J, Tse C (2015) Synchronization in directed complex networks using graph comparison tools. IEEE Trans Circuits I Regul Pap 62(4):1185–1194

    Article  MathSciNet  Google Scholar 

  25. Li Y, Wu X, Lu J, Lü J (2016) Synchronizability of duplex networks. IEEE Trans Circuits II Express Briefs 63(2):206–210

    Google Scholar 

  26. Yang X, Cao J, Long Y, Rui W (2010) Adaptive lag synchronization for competitive neural networks with mixed delays and uncertain hybrid perturbations. IEEE Trans Neural Netw 21(10):1656–1667

    Article  Google Scholar 

  27. Chen W, Lu X, Zheng W (2015) Impulsive stabilization and impulsive synchronization of discrete-time delayed neural networks. IEEE Trans Neural Netw Learn Syst 26(4):734–748

    Article  MathSciNet  Google Scholar 

  28. Han M, Zhang Y (2016) Complex function projective synchronization in drive-response complex-variable dynamical networks with coupling time delays. J Frankl Inst 353(8):1742–1758

    Article  MathSciNet  MATH  Google Scholar 

  29. Zhou W, Zhou X, Yang J, Liu Y, Zhang X, Ding X (2016) Exponential synchronization for stochastic neural networks driven by fractional Brownian motion. J Frankl Inst 353(8):1689–1712

    Article  MathSciNet  MATH  Google Scholar 

  30. Tong D, Zhang L, Zhou W, Zhou J, Xu Y (2016) Asymptotical synchronization for delayed stochastic neural networks with uncertainty via adaptive control. Int J Control Autom 14(3):706–712

    Article  Google Scholar 

  31. Gan Q, Lv T, Fu Z (2016) Synchronization criteria for generalized reaction-diffusion neural networks via periodically intermittent control. Chaos 26(4):1–11

    Article  MathSciNet  MATH  Google Scholar 

  32. Hu C, Yu J, Jiang H (2014) Finite-time synchronization of delayed neural networks with Cohen–Grossberg type based on delayed feedback control. Neurocomputing 143(16):90–96

    Article  Google Scholar 

  33. Li N, Cao J (2015) New synchronization criteria for memristor-based networks: adaptive control and feedback control schemes. Neural Netw 61:1–9

    Article  MATH  Google Scholar 

  34. Bao H, Park JH, Cao J (2015) Matrix measure strategies for exponential synchronization and anti-synchronization of memristor-based neural networks with time-varying delays. Appl Math Comput 270:543–556

    MathSciNet  MATH  Google Scholar 

  35. Mathiyalagan K, Anbuvithya R, Sakthivel R, Park JH, Prakash P (2016) Non-fragile \(H_{\infty }\) synchronization of memristor-based neural networks using passivity theory. Neural Netw 74:85–100

    Article  MATH  Google Scholar 

  36. Bao H, Park JH, Cao J (2015) Adaptive synchronization of fractional-order memristor-based neural networks with time delay. Nonlinear Dyn 82:1343–1354

    Article  MathSciNet  MATH  Google Scholar 

  37. Gao J, Zhu P, Alsaedi A, Alsaadi F, Hayat T (2017) A new switching control for finite-time synchronization of memristor-based recurrent neural networks. Neural Netw 86:1–9

    Article  Google Scholar 

  38. Cao J, Li R (2017) Fixed-time synchronization of delayed memristor-based recurrent neural networks. Sci China Inform Sci 60(3):1–15

    MathSciNet  Google Scholar 

  39. Bao H, Park JH, Cao J (2016) Exponential synchronization of coupled stochastic memristor-based neural networks with time-varying probabilistic delay coupling and impulsive delay. IEEE Trans Neural Netw Learn Syst 27(1):190–201

    Article  MathSciNet  Google Scholar 

  40. Zhang G, Hu J, Shen Y (2015) New results on synchronization control of delayed memristive neural networks. Nonlinear Dyn 81(3):1167–1178

    Article  MathSciNet  MATH  Google Scholar 

  41. Fox L, Mayers D, Ockendon J, Tayler A (1971) On a functional differential equation. IMA J Appl Math 8(3):271–307

    Article  MATH  Google Scholar 

  42. Dovrolis C, Stiliadis D, Ramanathan P (1999) Proportional differentiated services: delay differentiation and packet scheduling. Comput Commun Rev 29(4):109–120

    Article  Google Scholar 

  43. Maneyama Y, Kubo R (2014) QoS-aware cyclic sleep control with proportional-derivative controllers for energy-efficient PON systems. IEEE/OSA J Opt Commun Netw 6(11):1048–1058

    Article  Google Scholar 

  44. Zhou L (2016) Delay-dependent exponential stability of recurrent neural networks with Markovian jumping parameters and proportional delays. Neural Comput Appl 28(1):765–773

    Google Scholar 

  45. Zheng C, Li N, Cao J (2015) Matrix measure based stability criteria for high-order neural networks with proportional delay. Neurocomputing 149(3):1149–1154

    Article  Google Scholar 

  46. Zhou L (2013) Delay-dependent exponential stability of cellular neural networks with multi-proportional delays. Neural Process Lett 38(3):347–359

    Article  Google Scholar 

  47. Zhou L, Chen X, Yang Y (2014) Asymptotic stability of cellular neural networks with multiple proportional delays. Appl Math Comput 229(5):457–466

    MathSciNet  MATH  Google Scholar 

  48. Zhou L, Zhang Y (2016) Global exponential periodicity and stability of recurrent neural networks with multi-proportional delays. ISA Trans 60:89–95

    Article  Google Scholar 

  49. Zhou L (2015) Delay-dependent exponential synchronization of recurrent neural networks with multiple proportional delays. Neural Process Lett 42(3):619–632

    Article  Google Scholar 

  50. Zhou L (2015) Novel global exponential stability criteria for hybrid BAM neural networks with proportional delays. Neurocomputing 161(15):99–106

    Article  Google Scholar 

  51. Zhou L, Zhao Z (2016) Exponential stability of a class of competitive neural networks with multi-proportional delays. Neural Process Lett 44(3):651–663

    Article  Google Scholar 

  52. Filippov A (1988) Differential equations with discontinuous right-hand sides. Kluwer, Dordrecht

    Book  MATH  Google Scholar 

Download references

Acknowledgements

The work is supported by the National Science Foundation of China (No. 61374009), Project training of backbone teachers in colleges and universities of Tianjin (No. 043-135205GC38).

Author information

Authors and Affiliations

  1. School of Mathematics Science, Tianjin Normal University, Tianjin, 300387, China

    Lijuan Su & Liqun Zhou

Authors
  1. Lijuan Su
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Liqun Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Liqun Zhou.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Su, L., Zhou, L. Exponential synchronization of memristor-based recurrent neural networks with multi-proportional delays. Neural Comput & Applic 31, 7907–7920 (2019). https://doi.org/10.1007/s00521-018-3569-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-018-3569-z

Keywords

Search

Navigation