Abstract
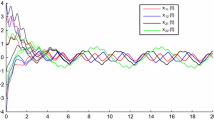
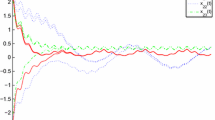
A model of shunting inhibitory cellular neural networks with mixed delays is proposed. Applying appropriate differential inequality techniques, several sufficient conditions are derived to ensure the existence and exponential stability of weighted pseudo-anti-periodic solutions for the proposed neural networks. Moreover, numerical examples are provided to show the validity and the advantages of the obtained results

Similar content being viewed by others
References
Bouzerdoum A, Pinter RB (1993) Shunting inhibitory cellular neural networks: derivation and stability analysis. IEEE Trans Circuits Syst 1 Fundam Theory Appl 40:215–221
Bouzerdoum A, Pinter RB (1991) Analysis and analog implementation of directionally sensitive shunting inhibitory cellular neural networks. Vis Inf Process Neurons Chips SPIE–1473:29–38
Bouzerdoum A, Pinter RB (1992) Nonlinear lateral inhibition applied to motion detection in the fly visual system. In: Pinter RB, Nabet B (eds) Nonlinear vision. CRC Press, Boca Raton, pp 423–450
Ou C (2009) Almost periodic solutions for shunting inhibitory cellular neural networks. Nonlinear Anal Real World Appl 10:2652–2658
Chen Z (2013) A shunting inhibitory cellular neural network with leakage delays and continuously distributed delays of neutral type. Neural Comput Appl 23:2429–2434
Wang W, Liu B (2014) Global exponential stability of pseudo almost periodic solutions for SICNNs with time-varying leakage delays. Abst Appl Anal 967328:1–17
Liu X (2015) Exponential convergence of SICNNs with delays and oscillating coefficients in leakage terms. Neurocomput 168:500–504
Zhao C, Wang Z (2015) Exponential convergence of a SICNN with leakage delays and continuously distributed delays of neutral type. Neural Process Lett 41:239–247
Jiang A (2015) Exponential convergence for shunting inhibitory cellular neural networks with oscillating coefficients in leakage terms. Neurocomput 165:159–162
Zhang A (2016) Pseudo almost periodic solutions for SICNNs with oscillating leakage coefficients and complex deviating arguments. Neural Process Lett. doi:10.1007/s11063-016-9518-x
Liu B (2016) Global exponential convergence of non-autonomous SICNNs with multi-proportional delays. Neural Comput Appl. doi:10.1007/s00521-015-2165-8
Liu B (2009) An anti-periodic LaSalle oscillation theorem for a class of functional differential equations. J Comput Appl Math 223:1081–1086
Li Y, Huang L (2009) Anti-periodic solutions for a class of Li\(\acute{e}\)nard-type systems with continuously distributed delays. Nonlinear Anal Real World Appl 10(4):2127–2132
Fan Q, Wang W, Yi X (2009) Anti-periodic solutions for a class of nonlinear nth-order differential equations with delays. J Comput Appl Math 230(2):762–769
Ou C (2008) Anti-periodic solution for high-order Hopfield neural networks. Comput Math Appl 56:1838–1844
Zhao C, Fan Q, Wang W (2010) Anti-periodic solutions for shunting inhibitory cellular neural networks with time-varying coefficients. Neural Process Lett 31:259–267
Gong S (2009) Anti-periodic solutions for a class of Cohen–Grossberg neural networks. Comput Math Appl 58:341–347
Wang W (2013) Anti-periodic solution for impulsive high-order Hopfield neural networks with time-varying delays in the leakage terms. Adv Differ Equ 2013(73):1–15
Peng L, Wang W (2013) Anti-periodic solutions for shunting inhibitory cellular neural networks with time-varying delays in leakage terms. Neurocomput 111(2):27–33
Zhou Q (2016) Anti-periodic solutions for cellular neural networks with oscillating coefficients in leakage terms. Int J Mach Learn Cyber. doi:10.1007/s13042-016-0531-1
Long Z (2016) New results on anti-periodic solutions for SICNNs with oscillating coefficients in leakage terms. Neurocomput 171(1):503–509
Al-Islam NS, Alsulami SM, Diagana T (2012) Existence of weighted pseudo anti-periodic solutions to some non-autonomous differential equations. Appl Math Comput 218:6536–6548
Acknowledgments
The authors would like to express their sincere appreciation to the editor and reviewers for their helpful comments in improving the presentation and quality of the paper. In particular, the authors express the sincere gratitude to Prof. Bingwen Liu (Jiaxing University) for the helpful discussion when this revision work was being carried out. This work was supported by the Natural Scientific Research Fund of Hunan Province of China (Grant Nos. 2016JJ6103, 2016JJ6104).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhou, Q., Shao, J. Weighted pseudo-anti-periodic SICNNs with mixed delays. Neural Comput & Applic 29, 865–872 (2018). https://doi.org/10.1007/s00521-016-2582-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-016-2582-3
Keywords
- Weighted pseudo-anti-periodic solution
- Shunting inhibitory cellular neural network
- Exponential stability
- Mixed delay