Skip to main content
SpringerLink
Log in

A feedback neural network for solving convex quadratic bi-level programming problems

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

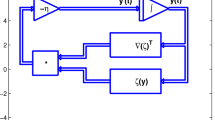
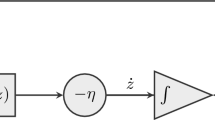
Abstract

In this paper, a feedback neural network model is proposed for solving a class of convex quadratic bi-level programming problems based on the idea of successive approximation. Differing from existing neural network models, the proposed neural network has the least number of state variables and simple structure. Based on Lyapunov theories, we prove that the equilibrium point sequence of the feedback neural network can approximately converge to an optimal solution of the convex quadratic bi-level problem under certain conditions, and the corresponding sequence of the function value approximately converges to the optimal value of the convex quadratic bi-level problem. Simulation experiments on three numerical examples and a portfolio selection problem are provided to show the efficiency and performance of the proposed neural network approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Bard J (1998) Practical bi-level optimization: algorithm and applications. Kluwer, Dordrecht

    Book  Google Scholar 

  2. Dempe S (2002) Foundation of bi-level programming. Kluwer, London

    Google Scholar 

  3. Lee ES, Shih HS (2001) Fuzzy and multi-level decision making: an interactive computational approach. Springer, London

    Book  Google Scholar 

  4. Bialas WF, Karwan MH (1982) On two-level optimization. IEEE Trans Autom Control 27:211–214

    Article  MATH  Google Scholar 

  5. Yang H, Bell MGH (1998) Models and algorithms for road network design: a review and some new developments. Transp Rev 18:257–278

    Article  Google Scholar 

  6. Ben-Ayed O, Blair O (1990) Computational difficulity of bi-level linear programming. Oper Res 38:556–560

    Article  MATH  MathSciNet  Google Scholar 

  7. Tank DW, Hopfield JJ (1986) Simple neural optimization networks: an A/D convert, signal decision circuit, and a linear programming circuit. IEEE Trans Circuits Syst CAS 33:533–541

    Article  Google Scholar 

  8. Chen K, Leung Y, Leung K, Gao X (2002) A neural network for solving nonlinear programming problems. Neural Comput Appl 11:103–111

    Article  Google Scholar 

  9. Leung Y, Chen K, Jiao Y, Gao X, Leung K (2001) A new gradient-based neural network for solving linear and quadratic programming problems. IEEE Trans Neural Netw 12:1074–1083

    Article  Google Scholar 

  10. Wen U, Lan K, Shih H (2009) A review of Hopfield neural networks for solving mathematical programming problems. Eur J Oper Res 198:675–687

    Article  MATH  MathSciNet  Google Scholar 

  11. Huang B, Zhang H, Gong D, Wang Z (2013) A new result for projection neural networks to solve linear variational inequalities and related optimization problems. Neural Comput Appl 23:357–362

    Article  Google Scholar 

  12. Xia Y, Wang J (1998) A general methodology for designing globally convergent optimizatin neural networks. IEEE Trans Neural Netw 9:1331–1343

    Article  Google Scholar 

  13. Huang T, Huang H, Li C (2008) Stability of periodic solution in fuzzy BAM neural networks with finite distributed delays. Neurocomputing 71:3064–3069

    Article  Google Scholar 

  14. Li C, Li CD, Huang T, Liao X (2011) Impulsive effects on stability of high-order BAM neural networks with time delays. Neurocomputing 74:1541–1550

    Article  Google Scholar 

  15. Wen S, Zeng Z, Huang T (2013) Dynamic behaviors of memristor-based delayed recurrent networks. Neural Comput Appl 23:815–821

    Article  Google Scholar 

  16. He X, Li C, Shu Y (2013) Fold-flip bifurcation analysis on a class of discrete-time neural network. Neural Comput Appl 22:375–381

    Article  Google Scholar 

  17. Morrison DD (1968) Optimization by least squares. SIAM J Numer Anal 5:83–88

    Article  MATH  MathSciNet  Google Scholar 

  18. Leung Y, Chen K, Gao X (2003) A high-performance feedback neural network for solving convex nonlinear programming problems. IEEE Trans Neural Netw 14:1469–1477

    Article  Google Scholar 

  19. Yang Y, Chao J (2008) A feedback neural network for solving convex constraint optimization problems. Appl Math Comput 201:340–350

    Article  MATH  MathSciNet  Google Scholar 

  20. Sheng Z, Lv Z, Xu R (1996) A new algorithm based on the frank-wolfe method and neural network for a class of bi-level decision making problems. Acta Automatica Sinica 22:657–665

    Google Scholar 

  21. Shih H, Wen U, Lee ES, Hsiao H (2004) A neural network approach to multiobjective and multilevel programming problems. Comput Math Appl 48:95–108

    Article  MATH  MathSciNet  Google Scholar 

  22. Lan K, Wen U, Lee ES (2007) A hybrid neural network approach to bi-level programming problems. Appl Math Lett 20:880–884

    Article  MATH  MathSciNet  Google Scholar 

  23. Lv Y, Hu T, Wang G, Wan Z (2008) A neural network approach for solving nonlinear bi-level programming problem. Comput Math Appl 58:2823–2829

    Article  MathSciNet  Google Scholar 

  24. Lv Y, Chen Z, Wan Z (2010) A neural network for solving a convex quadratic bi-level programming problem. J Comput Appl Math 234:505–511

    Article  MATH  MathSciNet  Google Scholar 

  25. Etoa Etoa JB (2011) Solving quadratic convex bi-level programming problems using a smoothing method. Appl Math Comput 217:6680–6690

    Article  MATH  MathSciNet  Google Scholar 

  26. An L, Quynh Y, Tao P (2012) A DC programming approach for a class of bi-level programming problems and its application in Portfolio Selection. Numer Algebra Control Optim 2:167–185

    Article  MATH  MathSciNet  Google Scholar 

  27. Facchinei F, Jiang H, Qi L (1999) A smoothing method for mathematical programming with equilibrium constraints. Math Program 85:107–134

    Article  MATH  MathSciNet  Google Scholar 

  28. LaSalle J (1976) The stability of dynamical systems. Springer, New York

    Book  MATH  Google Scholar 

  29. Ben-Ayed O (1988) Bi-level linear programming: analysis and application to the network design problem, PhD thesis, University of Illinois at Urbana-Champaign, IL

  30. Muu L, Quy N (2003) A global optimization method for solving convex quadratic bi-level programming problems. J Glob Optim 26:199–219

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

The authors are thankful to their editor and anonymous referees for their valuable comments and suggestions that have improved the quality of the paper significantly.

Author information

Authors and Affiliations

  1. School of Science, Information Technology and Engineering, University of Ballarat, Ballarat, VIC, 3353, Australia

    Jueyou Li, Chaojie Li & Zhiyou Wu

  2. Department of Mathematics, Chongqing Normal University, Chongqing, 400047, People’s Republic of China

    Jueyou Li & Zhiyou Wu

  3. Department of Computer Science, Chongqing University of Education, Chongqing, 400067, People’s Republic of China

    Junjian Huang

Authors
  1. Jueyou Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chaojie Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhiyou Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Junjian Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chaojie Li.

Additional information

This research was partially supported by KJ120616, cstc2013jjB00001 and SRF for ROCS, SEM.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, J., Li, C., Wu, Z. et al. A feedback neural network for solving convex quadratic bi-level programming problems. Neural Comput & Applic 25, 603–611 (2014). https://doi.org/10.1007/s00521-013-1530-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-013-1530-8

Keywords

Search

Navigation