Skip to main content
SpringerLink
Log in

The globally asymptotic stability analysis for a class of recurrent neural networks with delays

  • Extreme Learning Machine's Theory & Application
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

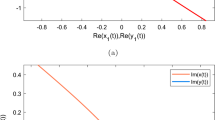
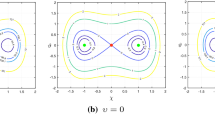
This paper considers the problem of global stability of neural networks with delays. By combining Lie algebra and the Lyapunov function with the integral inequality technique, we analyze the globally asymptotic stability of a class of recurrent neural networks with delays and give an estimate of the exponential stability. A few new sufficient conditions and criteria are proposed to ensure globally asymptotic stability of the equilibrium point of the neural networks. A few simulation examples are presented to demonstrate the effectiveness of the results and to improve feasibility.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Geman S, Bienenstock E, Doursat R (1992) Neural networks and the bias/variance dilemma. Neural Comput 4:1–58

    Article  Google Scholar 

  2. Grossberg S (1988) Nonlinear neural networks: principles, mechanisms, and architectures. Neural Netw 1:17–61

    Article  Google Scholar 

  3. Kerlirzin P, Vallet F (1993) Robustness in multilayer perceptrons. Neural Comput 5(3):473–482

    Article  Google Scholar 

  4. Lu W, Rong L, Chen T (2003) Global convergence of delayed dynamical systems [J]. Int J Neural Syst 13:1–12

    Article  Google Scholar 

  5. Li X, Huang L, Zhu H (2003) Global stability of cellular neural networks with constant and variable delays. Nonlinear Anal 53:319–333

    Article  MathSciNet  MATH  Google Scholar 

  6. Ren F, Cao J (2006) LMI-based criteria for stability of high-order neural networks with time-varying delay. Nonlinear Anal Real World Appl 7:967–979

    Article  MathSciNet  MATH  Google Scholar 

  7. Abarbanel HDI (1996) Analysis of observed chaotic data. Springer, New York

  8. Arik S, Tavsanoglu V (2000) On the global asymptotic stability of delayed cellular neural networks. IEEE Trans Circuits Syst I 47:571–574

    Article  MathSciNet  MATH  Google Scholar 

  9. Singh V (2007) Improved global robust stability criterion for delayed neural networks. Chaos Solitons Fractals 31:224–229

    Article  MathSciNet  MATH  Google Scholar 

  10. Arik S (2002) An improved global stability result for delayed cellular neural networks. IEEE Trans Circuits Syst-I 49:1211–1214

    Article  MathSciNet  Google Scholar 

  11. Arik S (2002) An analysis of global asymptotic stability of delayed cellular neural networks. IEEE Trans Neural Netw 13:1239–1242

    Article  Google Scholar 

  12. Arik S (2003) Global asymptotic stability of a larger class of neural networks with constant time delay. Phys Lett A 311:504–511

    Article  MATH  Google Scholar 

  13. Cao J (2001) Global stability conditions for delayed CNNs. IEEE Trans Circuits Syst I 48:1330–1333

    Article  MATH  Google Scholar 

  14. Huang H, Teng Z (2005) A new criterion on global exponential stability for cellular neural networks with multiple time-varying delays. Phys Lett A 338:461–471

    Article  Google Scholar 

  15. He Y, Wang Q, Wu M, Lin C (2006) Delay-dependent state estimation for delayed neural networks. IEEE Trans Neural Netw 17:1077–1081

    Article  MATH  Google Scholar 

  16. Arik S (2000) Global asymptotic stability of a class of dynamical neural networks. IEEE Trans Circuits Syst I 47:568–571

    Article  MathSciNet  MATH  Google Scholar 

  17. Meyer-Bäse A, Sergei S, Pilyugin SS (2003) Global asymptotic stability of a class of dynamical neural networks. Int J Neural Syst 13(1):47–53

    Article  Google Scholar 

  18. Liao X, Chen G, Sanchez EN (2002) LMI-based approach for asymptotic stability analysis of delayed neural networks. IEEE Trans Circuits Syst I 49:1033–1039

    Article  MathSciNet  Google Scholar 

  19. Cao J, Wang J (2003) Global asymptotic stability of a general class of recurrent neural networks with time-varying delays. IEEE Trans Circuits Syst I 50:34–44

    Article  MathSciNet  Google Scholar 

  20. Sagle A, Walde R (1973) Introduction to Lie groups and Lie algebras. Academic Press, New York

    MATH  Google Scholar 

  21. Chu T, Zhang C, Zhang Z (2003) Necessary and sufficient condition for absolute stability of normal neural networks. Neural Netw 16:1223–1227

    Article  Google Scholar 

  22. Matsuoka K (1992) Stability conditions for nonlinear continuous neural networks with asymmetric connection weights. Neural Netw 5:495–500

    Article  Google Scholar 

  23. Chu T, Zhang C (2007) New necessary and sufficient conditions for absolute stability of neural networks. Neural Netw 20:94–101

    Article  MATH  Google Scholar 

  24. Xu S, Lam J (2006) A new approach to exponential stability analysis of neural networks with time-varying delays. Neural Netw 19:76–83

    Article  MATH  Google Scholar 

Download references

Acknowledgments

This work was supported by the National Natural Science Foundation of China (50975059/61005080), the Doctoral Foundation of China (20100480994), the Doctoral Foundation of Heilongjiang Province, and the“111” Project (B07018).

Author information

Authors and Affiliations

  1. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin, 150001, China

    Xingguo Song, Haibo Gao, Liang Ding & Minghui Hao

  2. Yanshan University, Qinhuangdao, 066004, China

    Deyou Liu

Authors
  1. Xingguo Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Haibo Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Liang Ding
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Deyou Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Minghui Hao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xingguo Song.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Song, X., Gao, H., Ding, L. et al. The globally asymptotic stability analysis for a class of recurrent neural networks with delays. Neural Comput & Applic 22, 587–595 (2013). https://doi.org/10.1007/s00521-012-0888-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-012-0888-3

Keywords

Search

Navigation