Abstract
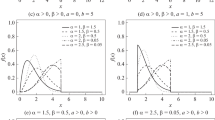
In this paper, we propose a new lifetime distribution called transmuted record type Lindley (TRTL). Some mathematical properties of the TRTL distribution are discussed namely, density shapes, moments, variance, the coefficient of skewness, coefficient of kurtosis, and moment generating function. We use the maximum likelihood method for point and interval estimation. The asymptotic confidence intervals based on maximum likelihood estimators (MLEs) are derived. A extensive Monte Carlo simulation study is performed to evaluate the performances of the MLEs with respect to mean squared error (MSE) criterion. Finally, three COVID-19 patient data examples are considered to illustrate the usefulness of the introduced model in modelling real-life data. According to the results of real-world data examples, we observe the best-fitted model is the TRTL among the competitor models.








Similar content being viewed by others
Data Availability
Data for this work were obtained from the web (accessed from https://data.gov.il/dataset/covid-19).
References
Afify AZ, Cordeiro GM, Nadarajah S, Yousof HM, Ozel G, Nofal ZM, Altun E (2016) The complementary geometric transmuted-G family of distributions: model, properties and application. Hacettepe J Math Stat 47(5):1348–1374
Balakrishnan N, He M (2021) A record-based transmuted family of distributions. In: Advances in statistics-theory and applications. Springer, pp 3–24. https://doi.org/10.1007/978-3-030-62900-71(2021)
Bhatti FA, Ali A (2019) Characterizations of transmuted exponentiated Pareto-I (TEP-I) distribution. Int J Mod Math Sci 17(1):1–20
Bhatti FA, Hamedani GG, Ali A, Ahmad M (2018a) Some characterizations of transmuted modified Burr III distribution. Asian J Probab Stat, pp 1–9
Bhatti FA, Hamedani GG, Korkmaz MÇ, Ahmad M (2018b) The transmuted geometric-quadratic hazard rate distribution: development, properties, characterizations and applications. J Stat Distrib Appl 5(1):1–23 https://doi.org/10.1186/s40488-018-0085-8
Butt NS, Haq MA, Usman RM, Fattah AA (2016) Transmuted power function distribution. Gazi Univ J Sci 29(1):177–185
Elgarhy M, Elbatal I, Haq MA, Hassan AS (2018) Transmuted Kumaraswamy quasi Lindley distribution with applications. Ann Data Sci 5(4):565–581
Gradshteyn I, Ryzhik IM (2000) Table of integrals, series, and products, 6th edn. Academic Press, San Diego
Haq MA (2016) Transmuted exponentiated inverse Rayleigh distribution. J Stat Appl Prob 5(2):337–343
Korkmaz MC, Hamedani GG (2020) An alternative distribution to Lindley and Power Lindley distributions with characterizations, different estimation methods and data applications. Math Slov 70(4):953–978
Korkmaz MC, Yousof HM, Hamedani GG (2018) The exponential Lindley odd log-logistic-G family: properties, characterizations and applications. J Stat Theory Appl 17(3):554–571
Korkmaz MÇ, Altun E, Yousof HM, Hamedani GG (2019) The odd power Lindley generator of probability distributions: properties, characterizations and regression modeling. Int J Stat Probab 8(2):70–89
Mansour MM, Abd Elrazik EM, Afify AZ, Ahsanullah M, Altun E (2019) The transmuted transmuted-G family: properties and applications. J Nonlinear Sci Appl 12:217–229
Nofal ZM, El Gebaly YM, Altun E, Alizadeh M, Butt NS (2017) The transmuted geometric-Weibull distribution: properties, characterizations and regression models. Pak J Stat Oper Res 13(2):395–416
Shaked M, Shanthikumar JG (1994) Stochastic orders and their applications. Academic Press, London
Shaw WT, Buckley IR (2009) The alchemy of probability distributions: beyond Gram-Charlier expansions, and a skew-kurtotic-normal distribution from a rank transmutation map. arXiv preprint arXiv:0901.0434
Smith RM, Bain LJ (1975) An exponential power life-testing distribution. Commun Stat Theory Methods 4(5):469–481
Tahir A, Akhter AS, Haq MA (2018) Transmuted New Weibull-Pareto Distribution and its Applications. Appl Appl Math Int J 13(1):30–46
Tanış C (2021) Transmuted lower record type power function distribution. J Sci Arts 21(4):951–960
Tanış C (2022) Transmuted lower record type inverse Rayleigh distribution: estimation, characterizations and applications. Ricerche Mat 71(2):777–802
Tanış C, Saraçoğlu B (2022) On the record-based transmuted model of Balakrishnan and He based on Weibull distribution. Commun Stat-Simul Comput 51(8):4204–4224
Tanış C, Saraçoğlu B, Kus C, Pekgor A, Karakaya K (2021) Transmuted lower record type Fréchet distribution with lifetime regression analysis based on type I-censored data. J Stat Theory Appl 20(1):86–96
ul Haq MA, Elgarhy M, Hashmi S, Ozel G, ul Ain Q (2018) Transmuted Weibull power function distribution: its properties and applications. J Data Sci 16(2):397–418
URL-1. https://data.gov.il/dataset/Covid-19, Accessed 25 Jan 2021
Usman RM, Bursa N, Özel G (2018) Exponentiated transmuted power function distribution: theory and applications. Gazi Univ J Sci 31(2):660–675
Yadav AS, Singh SK, Singh U (2018) Statıstıcal propertıes and estımatıon procedure for transmuted inverted exponentıal dıstrıbutıon: applıcatıon to bladder cancer data. J Reliab Stat Stud 15:81–98
Funding
The author states no funding associated with the work featured in this article.
Author information
Authors and Affiliations
Contributions
CT contributed to introduction, transmuted record type method (TRTM), transmuted record type Lindley (TRTL) distribution, maximum likelihood estimation, simulation study, real data applications, and conclusion sections.
Corresponding author
Ethics declarations
Conflict of interest
C. Tanıs state that there are no conflicts of interest.
Ethical approval
No ethical violations were made in this study. The data is sourced anonymously, which can be accessed by anyone from https://data.gov.il/dataset/covid-19).
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Tanış, C. A new Lindley distribution: applications to COVID-19 patients data. Soft Comput 28, 2863–2874 (2024). https://doi.org/10.1007/s00500-023-09339-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-023-09339-7