Skip to main content
SpringerLink
Log in

Optimal design of adaptive neuro-fuzzy inference system using PSO and ant colony optimization for estimation of uncertain observed values

  • Fuzzy systems and their mathematics
  • Published:
Soft Computing Aims and scope Submit manuscript

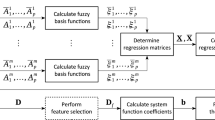
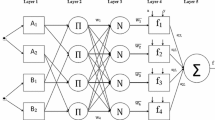
Abstract

This paper aims to address uncertainty in practical applications that the experimental observations and measurements have nature of inhomogeneity, randomness, and imprecision. This study employs a new method for regression model prediction in an uncertain environment and presents fuzzy parameter estimation of fuzzy regression models using triangular fuzzy numbers. These estimation methods are obtained by new learning algorithms in which linear programming is used. In this study, the new algorithm is a combination of a fuzzy rule-based system, on the basis of particle swarm optimization (PSO) and ant colony optimization ACOR. In the adaptive neuro-fuzzy inference system method, the output is crisp. In this research, a hybrid algorithm has been proposed to get the fuzzy output based on linear programming. Meta-heuristic algorithms have been used to reduce the error in the proposed methods based on PSO and ACOR. In addition, two simulation and two practical examples in the field of machining process are applied to indicate the performance of the proposed methods in dealing with crisp input and fuzzy output (CIFO) problems where the observed output variables have the nature of inhomogeneity, randomness, and imprecision. Finally, the results of the proposed algorithms are evaluated. Based on examples, the proposed method is more accurate than the LP and FWLP methods but is not more complicated than the FWLP in computations. Using paired t test, a significant difference was shown between the proposed methods and previous methods, such as LP and FWLP, but there was no significant difference between the two proposed methods ACOR and PSO.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availability

Enquiries about data availability should be directed to the authors.

References

  • Abed-algun BH, Paul DJ (2020) Hybridizing the cuckoo search algorithm with different mutation operators for numerical optimization problems J. Intell Syst 29(1):1043–1062

    Google Scholar 

  • Alex R (2006) A new kind of fuzzy regression modeling and its combination with fuzzy inference. Soft Comput 10(7):618–622

    Google Scholar 

  • Benardos PG, Mosialos S, Vosniakos GC (2006) Prediction of workpiece elastic deflections under cutting forces in turning. Robot Comput Integr Manuf 5(22):505–514

    Google Scholar 

  • Boothroyd G, Knight WA (2005) Fundamentals of machining and machine tools. Taylor and Francis, London, pp 166–173

    Google Scholar 

  • Cheng CB, Lee ES (1999) Applying fuzzy adaptive network to fuzzy regression analysis. Comput Math Appl 38(2):123–140

    MathSciNet  Google Scholar 

  • Chukhrova N, Johannssen A (2019) Fuzzy regression analysis: systematic review and bibliography. Appl Soft Comput 84:105708

    Google Scholar 

  • D’Urso P (2003) Linear regression analysis for fuzzy/crisp input and fuzzy/crisp output. Comput Stat Data Anal 42:47–72

    MathSciNet  Google Scholar 

  • Danesh S (2018) Fuzzy parameters estimation via hybrid methods. Hacet J Math Stat 47(6):1605–1624

    MathSciNet  Google Scholar 

  • Danesh M, Danesh S (2020) A combinatorial algorithm for fuzzy parameter estimation with application to uncertain measurements. J AI Data Min 8(4):525–533

    Google Scholar 

  • Danesh M, Khalili K (2015) Determination of tool wear in turning process using undecimated wavelet transform and textural features. Procedia Technol 19:98–105

    Google Scholar 

  • Danesh S, Farnoosh R, Razzaghnia T (2016) Fuzzy nonparametric regression based on an adaptive neuro-fuzzy inference system. Neurocomputing 173:1450–1460

    Google Scholar 

  • Danesh M, Danesh S, Razzaghnia T, Maleki A (2021) Prediction of fuzzy nonparametric regression function: a comparative study of a new hybrid method and smoothing methods. Glob Anal Discrete Math 6(1):143–177

    Google Scholar 

  • Dastranj MR, Ebrahimi E, Changizi N, Sameni E (2011) Control DC motorspeed with adaptive neuro-fuzzy control. Aust J Basic Appl Sci 5:1499–1504

    Google Scholar 

  • Diamond P (1988) Fuzzy least squares. Inf Sci 46(3):141–157

    MathSciNet  Google Scholar 

  • Dunyak JP, Wunsch D (2000) Fuzzy regression by fuzzy number neural networks. Fuzzy Sets Syst 112(3):371–380

    MathSciNet  Google Scholar 

  • Eberhart R, Kennedy J (1995) Particle swarm optimization. In: International conference of neural networks, Perth, Australia

  • Faes M, Moens D (2020) Recent trends in the modeling and quantification of non-probabilistic uncertainty. Arch Comput Methods Eng 27:633–671

    MathSciNet  Google Scholar 

  • Fan YR, Huang GH, Yang AL (2013) Generalized fuzzy linear programming for decision making under uncertainty. Feasibility of fuzzy solutions and solving approach. Inf Sci 241:12–27

    MathSciNet  Google Scholar 

  • Ferrero A, Salicone S ( 2007) Modeling and processing measurement uncertainty within the theory of evidence: mathematics of random–fuzzy variables. IEEE Trans Instrum Meas 3(50):704–716

    Google Scholar 

  • Fontes RM, Fontes CH, Kalid RA (2012) Dynamic model identification with uncertain process variables using fuzzy inference system. Comput Aided Chem Eng 31:955–959

    Google Scholar 

  • He YL, Wei CH, Long H, Ashfaq RAR, Huang JZ (2017) Random weight network-based fuzzy nonlinear regression for trapezoidal fuzzy number data. Appl Soft Comput 70:959–979

    Google Scholar 

  • Hidalgo D, Melin P, Castillo O (2012) An optimization method for designing type-2 fuzzy inference systems based on the footprint of uncertainty using genetic algorithms. Expert Syst Appl 39(4):4590–4598

    Google Scholar 

  • Hong DH, Hwang C (2004) Extended fuzzy regression model using regularization method. Inf Sci 164:31–46

    MathSciNet  Google Scholar 

  • Hong DH, Song JK, Young H (2001) Fuzzy least-squares linear regression analysis using shape preserving operations. Inf Sci 138:185–193

    MathSciNet  Google Scholar 

  • Ishibuchi H, Tanaka H (1992) Fuzzy regression analysis using neural networks. Fuzzy Sets Syst 50:257–265

    MathSciNet  Google Scholar 

  • Ishibuchi H, Kwon K, Tanaka H (1995) A learning algorithm of fuzzy neural networks with triangular fuzzy weights. Fuzzy Sets Syst 71:277–293

    Google Scholar 

  • Isukapalli SS, Roy A, Georgopoulos PG (1998) Stochastic response surface methods (SRSMs) for uncertainty propagation: application to environmental and biological systems. Risk Anal 18(3):351–363

    Google Scholar 

  • Jang JSR (1993) ANFIS: adaptive-network-based fuzzy inference system. IEEE Trans Syst Man Cybern 23(3):665–685

    Google Scholar 

  • Karaboga D, Kaya E (2019) Adaptive network based fuzzy inference system (ANFIS) training approaches: a comprehensive survey. Artif Intell Rev 52:2263–2293

    Google Scholar 

  • Kartalopous S (1996) Understanding neural networks and fuzzy logic. IEEE Press, New York

    Google Scholar 

  • Khalili K, Danesh M (2015) Identification of vibration level in metal cutting using undecimated wavelet transform and gray-level co-occurrence matrix texture features. Proc Inst Mech Eng B J Eng Manuf 229(2):786–804

    Google Scholar 

  • Mendel JM (2000) Uncertainty, fuzzy logic, and signal processing. Sign Proces 6(80):913–933

    Google Scholar 

  • Mosleh M, Otadi M, Abbasbandy S (2010) Evaluation of fuzzy regression models by fuzzy neural network. J Comput Appl Math 234(3):825–834

    MathSciNet  Google Scholar 

  • Mosleh M, Otadi M, Abbas bandy S (2011) Fuzzy polynomial regression with fuzzy neural networks. Appl Math Model 35(11):5400–5412

    MathSciNet  Google Scholar 

  • Mosleh M, Allahviranloo T, Otadi M (2012) Evaluation of fully fuzzy regression models by fuzzy neural network. Neural Comput Appl 21(1):105–112

    Google Scholar 

  • Naderkhani R, Behzad MH, Razzaghnia T (2021) Fuzzy regression analysis based on fuzzy neural networks using trapezoidal data. Int J Fuzzy Syst 23:1267–1280

    Google Scholar 

  • Okwu MO, Adetunji O (2018) A comparative study of artificial neural network (ANN) and adaptive neuro-fuzzy inference system (ANFIS) models in distribution system with nondeterministic inputs. Int J Eng Bus Manag 10:184797901876842. https://doi.org/10.1177/1847979018768421

    Article  Google Scholar 

  • Otadi M (2014) Fully fuzzy polynomial regression with fuzzy neural networks. Neurocomputing 142:486–493

    Google Scholar 

  • Phan AV, Baron L, Mayer JRR, Cloutier G (2003) Finite element and experimental studies of diametral errors in cantilever bar turning. Appl Math Model 2(27):221–232

    Google Scholar 

  • Qiang LZ (2000) Finite difference calculations of the deformations of multi-diameter workpieces during turning. J Mater Process Technol 3(98):310–316

    Google Scholar 

  • Rabiei MR, Arashi M, Farrokhi M (2019) Fuzzy ridge regression with fuzzy input and output. Soft Comput 23:12189–12198

    Google Scholar 

  • Razzaghnia T, Danesh S (2015) Nonpzarametric regression with trapezoidal fuzzy data. Int J Recent Innov Trends Comput Commun (IJRITCC) 3(6):3826–3831

    Google Scholar 

  • Razzaghnia T, Danesh S, Maleki A (2011) Hybrid fuzzy regression with trapezoidal fuzzy data. Proc SPIE 8349:834921

    Google Scholar 

  • Sarma PMMS, Karunamoothy L, Palanikumar K (2009) Surface roughness parameters evaluation in machining GFRP composites by PCD tool using digital image processing. J Reinf Plast Compos 28:1567–1585

    Google Scholar 

  • Socha K, Dorigo M (2008) Ant colony optimization for continuous domains. Eur J Oper Res 3(185):1155–1173

    MathSciNet  Google Scholar 

  • Sotoudeh-Anvari A (2020) A critical review on theoretical drawbacks and mathematical incorrect assumptions in fuzzy OR methods: review from 2010 to 2020. Appl Soft Comput J 93:106354

    Google Scholar 

  • Tanaka H (1987) Fuzzy data analysis by possibilistic linear models. Fuzzy Sets Syst 24(3):363–375

    MathSciNet  Google Scholar 

  • Tanaka H, Watada J (1988) Possibilistic linear systems and their application to the linear regression model. Fuzzy Sets Syst 27(3):275–289

    MathSciNet  Google Scholar 

  • Tanaka H, Uejimas S, Asia K (1982) Linear regression analysis with fuzzy model. IEEE Trans Syst Man Cybern 12:903–907

    Google Scholar 

  • Tanaka H, Hayashi I, Watada J (1989) Possibilistic linear regression analysis for fuzzy data. Eur J Oper Res 40(3):389–396

    MathSciNet  Google Scholar 

  • Wang C, Matthies HG (2019) Epistemic uncertainty-based reliability analysis for engineering system with hybrid evidence and fuzzy variables. Comput Methods Appl Mech Eng 355:438–455

    MathSciNet  Google Scholar 

  • Wang C, Matthies HG (2021) Coupled fuzzy-interval model and method for structural response analysis with non-probabilistic hybrid uncertainties. Fuzzy Sets Syst 417:171–189

    MathSciNet  Google Scholar 

  • Wu HC (2008) Fuzzy linear regression model based on fuzzy scalar product. Soft Comput 12:469–477

    Google Scholar 

  • Wu X, Xie Z, Tomasz Kozlowski AF (2021) A comprehensive survey of inverse uncertainty quantification of physical model parameters in nuclear system thermal–hydraulics codes. Nuclear Eng Des 384:111460

    Google Scholar 

  • Yagiz S, Gokceoglu C (2010) Application of fuzzy inference system and nonlinear regression models for predicting rock brittleness. Expert Syst Appl 37(3):2265–2272

    Google Scholar 

  • Zadeh A (1965) Fuzzy sets. Inf Control 8:338–353

    Google Scholar 

  • Zhang C, Guo P (2018) FLFP: a fuzzy linear fractional programming approach with double-sided fuzziness for optimal irrigation water allocation. Agric Water Manag 199:105–119

    Google Scholar 

  • Zuo H, Zhang G, Pedrycz W, Behbood V, Lu J (2017) Fuzzy regression transfer learning in Takagi–Sugeno fuzzy models. IEEE Trans Fuzzy Syst 25(6):1795–1807

    Google Scholar 

Download references

Funding

The authors have not disclosed any funding.

Author information

Authors and Affiliations

  1. Buein Zahra Technical University, Buein Zahra, Ghazvin, Iran

    Mahdi Danesh

  2. Samaneh Yaran Danesh Electronic, Tabriz, Iran

    Sedigheh Danesh

Authors
  1. Mahdi Danesh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sedigheh Danesh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sedigheh Danesh.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

This research does not involve human nor animals.

Informed consent

Informed consent was obtained from all individual participants included in the study.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Danesh, M., Danesh, S. Optimal design of adaptive neuro-fuzzy inference system using PSO and ant colony optimization for estimation of uncertain observed values. Soft Comput 28, 135–152 (2024). https://doi.org/10.1007/s00500-023-09194-6

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-023-09194-6

Keywords

Search

Navigation