Skip to main content
SpringerLink
Log in

Pattern recognition and medical diagnosis based on trigonometric similarity measures for bipolar complex fuzzy soft sets

  • Fuzzy systems and their mathematics
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

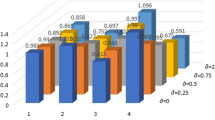
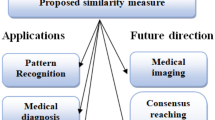
Bipolar complex fuzzy soft sets, one of the substantial notions, generalize the notions of bipolar complex fuzzy sets and soft sets. The notion of bipolar complex fuzzy soft sets is a significant tool to cope with the awkward and complicated information involving the second dimension, i.e., unreal part, both positive and negative opinions, and the parameters. Further, similarity measures play an important role in various fields such as data mining, machine learning, information retrieval, and natural language processing. They are used to measure the degree of similarity or dissimilarity between two or more objects, documents, images, or any other type of data. Consequently, in this script, we diagnose trigonometric similarity measures like generalized cosine similarity measure, generalized tangent similarity measure and generalized cotangent similarity measure, and generalized hybrid trigonometric similarity measure in the environment of bipolar complex fuzzy soft sets. Furthermore, we also discuss the weighted generalized cosine similarity measure, weighted generalized tangent similarity measure, weighted generalized cotangent similarity measure, and weighted generalized hybrid trigonometric similarity measure for bipolar complex fuzzy soft sets. After that, through the diagnosed similarity measures, we analyze real-life dilemmas like pattern recognition and medical diagnosis to portray the applicability and benefits of the diagnosed similarity measures in the real world. At the end of this study, we show the superiority and supremacy of the analyzed trigonometric similarity measures by doing their analysis with certain prevailing similarity measures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data availability

The data utilized in this manuscript are hypothetical and artificial, and one can use these data before prior permission by just citing this manuscript.

References

  • Abdullah S, Aslam M, Ullah K (2014) Bipolar fuzzy soft sets and its applications in decision making problem. J Intell Fuzzy Syst 27(2):729–742

    MathSciNet  MATH  Google Scholar 

  • Abid MN, Yang MS, Karamti H, Ullah K, Pamucar D (2022) Similarity measures based on T-spherical fuzzy information with applications to pattern recognition and decision making. Symmetry 14(2):410

    Google Scholar 

  • Adam F, Hassan N (2014) Q-fuzzy soft set. Appl Math Sci 8(174):8689–8695

    Google Scholar 

  • Ahmmad J, Mahmood T, Chinram R, Iampan A (2021) Some average aggregation operators based on spherical fuzzy soft sets and their applications in multi-criteria decision making. AIMS Math 6(7):7798–7833

    MathSciNet  MATH  Google Scholar 

  • Akram M, Akmal R (2016) Application of bipolar fuzzy sets in graph structures. Appl Comput Intell Soft Computng

  • Akram M, Arshad M (2020) Bipolar fuzzy TOPSIS and bipolar fuzzy ELECTRE-I methods to diagnosis. Comput Appl Math 39(1):1–21

    MathSciNet  Google Scholar 

  • Akram M, Waseem N (2018) Novel applications of bipolar fuzzy graphs to decision making problems. J Appl Math Comput 56(1):73–91

    MathSciNet  MATH  Google Scholar 

  • Akram M, Alshehri N, Davvaz B, Ashraf A (2016) Bipolar fuzzy digraphs in decision support systems. J Multiple-Valued Logic Soft Comput 27

  • Akram M, Allahviranloo T, Pedrycz W, Ali M (2021a) Methods for solving LR-bipolar fuzzy linear systems. Soft Comput 25(1):85–108

    MATH  Google Scholar 

  • Akram M, Amjad U, Davvaz B (2021b) Decision-making analysis based on bipolar fuzzy N-soft information. Comput Appl Math 40(6):1–39

    MathSciNet  MATH  Google Scholar 

  • Akram M, Shabir M, Al-Kenani AN, Alcantud JCR (2021c) Hybrid decision-making frameworks under complex spherical fuzzy N-soft sets. J Math 2021:1–46

    MathSciNet  MATH  Google Scholar 

  • Akram M, Ali M, Allahviranloo T (2021d) Solution of complex bipolar fuzzy linear system. In: Progress in intelligent decision science: proceeding of IDS 2020: (pp. 899–927). Cham: Springer

  • Akram M, Ali M, Allahviranloo T (2022a) A method for solving bipolar fuzzy complex linear systems with real and complex coefficients. Soft Comput 26(5):2157–2178

    Google Scholar 

  • Akram M, Amjad U, Alcantud JCR, Santos-García G (2022b) Complex fermatean fuzzy N-soft sets: a new hybrid model with applications. J Ambient Intell Humanized Comput, 1–34

  • Alcantud JCR (2016) A novel algorithm for fuzzy soft set based decision making from multi observer input parameter data set. Inf Fusion 29:142–148

    Google Scholar 

  • Alghamdi MA, Alshehri NO, Akram M (2018) Multi-criteria decision-making methods in bipolar fuzzy environment. Int J Fuzzy Syst 20(6):2057–2064

    Google Scholar 

  • Ali MI, Feng F, Liu X, Min WK, Shabir M (2009) On some new operations in soft set theory. Comput Math Appl 57(9):1547–1553

    MathSciNet  MATH  Google Scholar 

  • Ali Z, Mahmood T, Yang MS (2020) TOPSIS method based on complex spherical fuzzy sets with Bonferroni mean operators. Mathematics 8(10):1739

    Google Scholar 

  • Ali Z, Mahmood T, Ullah K, Khan Q (2021) Einstein geometric aggregation operators using a novel complex interval-valued Pythagorean fuzzy setting with application in green supplier chain management. Rep Mech Eng 2(1):105–134

    Google Scholar 

  • Alkhazaleh S, Salleh AR, Hassan N (2011) Possibility fuzzy soft set. Adv Decis Sci

  • Arya V, Kumar S (2020) Fuzzy entropy measure with an applications in decision making under bipolar fuzzy environment based on TOPSIS method. Int J Inf Manage Sci 31(2):99–121

    MATH  Google Scholar 

  • Atanassov KT (1999). Intuitionistic fuzzy sets. In: Intuitionistic fuzzy sets. Physica, Heidelberg, pp 1–137

  • Babitha KV, Sunil J (2010) Soft set relations and functions. Comput Math Appl 60(7):1840–1849

    MathSciNet  MATH  Google Scholar 

  • Bi L, Dai S, Hu B (2018) Complex fuzzy geometric aggregation operators. Symmetry 10(7):251

    Google Scholar 

  • Bi L, Dai S, Hu B, Li S (2019) Complex fuzzy arithmetic aggregation operators. J Intell Fuzzy Syst 36(3):2765–2771

    Google Scholar 

  • Boora R, Tomar VP (2022) Two trigonometric intuitionistic fuzzy similarity measures. Int J Decis Support Syst Technol 14(1):1–23

    Google Scholar 

  • Bustince H, Barrenechea E, Pagola M (2007) Image thresholding using restricted equivalence functions and maximizing the measures of similarity. Fuzzy Sets Syst 158(5):496–516

    MathSciNet  MATH  Google Scholar 

  • Bustince H, Barrenechea E, Pagola M (2008) Relationship between restricted dissimilarity functions, restricted equivalence functions and normal EN-functions: image thresholding invariant. Pattern Recognit Lett 29(4):525–536

    Google Scholar 

  • Çağman N, Karataş S (2013) Intuitionistic fuzzy soft set theory and its decision making. J Intell Fuzzy Syst 24(4):829–836

    MathSciNet  MATH  Google Scholar 

  • Campos ACSM, Mareschal B, de Almeida AT (2015) Fuzzy flow sort: an integration of the flow sort method and fuzzy set theory for decision making on the basis of inaccurate quantitative data. Inf Sci 293:115–124

    Google Scholar 

  • Feng F, Jun YB, Liu X, Li L (2010) An adjustable approach to fuzzy soft set based decision making. J Comput Appl Math 234(1):10–20

    MathSciNet  MATH  Google Scholar 

  • Guo W, Bi L, Hu B, Dai S (2020) Cosine similarity measure of complex fuzzy sets and robustness of complex fuzzy connectives. Math Probl Eng

  • Jana C, Pal M, Wang JQ (2019) Bipolar fuzzy Dombi aggregation operators and its application in multiple-attribute decision-making process. J Ambient Intell Humaniz Comput 10(9):3533–3549

    Google Scholar 

  • Lee SH, Pedrycz W, Sohn G (2009) Design of similarity and dissimilarity measures for fuzzy sets on the basis of distance measure. Int J Fuzzy Syst 11(2)

  • Liang Z, Shi P (2003) Similarity measures on intuitionistic fuzzy sets. Pattern Recognit Lett 24(15):2687–2693

    MATH  Google Scholar 

  • Liu P, Ali Z, Mahmood T (2020) The distance measures and cross-entropy based on complex fuzzy sets and their application in decision making. J Intell Fuzzy Syst 39(3):3351–3374

    Google Scholar 

  • Li J, Deng G, Li H, Zeng W (2012) The relationship between similarity measure and entropy of intuitionistic fuzzy sets. Inf Sci 188:314–321

    MathSciNet  MATH  Google Scholar 

  • Mahmood T (2020) A novel approach towards bipolar soft sets and their applications. J Math

  • Mahmood T (2022) A method to multi-attribute decision making technique based on Dombi aggregation operators under bipolar complex fuzzy information. Comput Appl Math 41(1):1–23

    MathSciNet  MATH  Google Scholar 

  • Mahmood T, Ur Rehman U (2022) A novel approach towards bipolar complex fuzzy sets and their applications in generalized similarity measures. Int J Intell Syst 37(1):535–567

    Google Scholar 

  • Mahmood T, Ali Z (2021) A novel complex fuzzy N-soft sets and their decision-making algorithm. Complex Intell Syst 7(5):2255–2280

    Google Scholar 

  • Mahmood T, Rehman UU, Ahmmad J, Santos-García G (2021a) Bipolar complex fuzzy Hamacher aggregation operators and their applications in multi-attribute decision making. Mathematics 10(1):23

    Google Scholar 

  • Mahmood T, Ur Rehman U, Ali Z, Mahmood T (2021b) Hybrid vector similarity measures based on complex hesitant fuzzy sets and their applications to pattern recognition and medical diagnosis. J Intell Fuzzy Syst 40(1):625–646

    Google Scholar 

  • Mahmood T, Ali Z (2022) Fuzzy superior Mandelbrot sets. Soft Comput 26(18):9011–9020

    Google Scholar 

  • Mahmood T, Rehman UU, Ali Z, Aslam M, Chinram R (2022a) Identification and classification of aggregation operators using bipolar complex fuzzy settings and their application in decision support systems. Mathematics 10(10):1726

    Google Scholar 

  • Mahmood T, Rehman UU, Jaleel A, Ahmmad J, Chinram R (2022b) Bipolar complex fuzzy soft sets and their applications in decision-making. Mathematics 10(7):1048

    Google Scholar 

  • Mahmood T, Rehman UU, Ali Z, Haleemzai I (2023) Analysis of TOPSIS techniques based on bipolar complex fuzzy N‐soft setting and their applications in decision‐making problems. CAAI Trans Intell Technol

  • Maji PK, Biswas R, Roy AR (2001) Fuzzy soft set theory. J Fuzzy Math 3(9):589–602

    MATH  Google Scholar 

  • Molodtsov D (1999) Soft set theory—first results. Comput Math Appl 37(4–5):19–31

    MathSciNet  MATH  Google Scholar 

  • Nguyen VU (1985) Some fuzzy set applications in mining geo mechanics. In: International Journal of Rock Mechanics and Mining Sciences & Geo mechanics Abstracts, 22(6): 369–379. Pergamon

  • Patrascu V (2015) Similarity, cardinality and entropy for bipolar fuzzy set in the framework of penta-valued representation. arXiv preprint arXiv:1506.02060

  • Rajeshwari M, Murugesan R, Venkatesh KA (2020) Distance between bipolar fuzzy sets. Int J Eng Res Technol 9(4)

  • Ramot D, Milo R, Friedman M, Kandel A (2002) Complex fuzzy sets. IEEE Trans Fuzzy Syst 10(2):171–186

    Google Scholar 

  • Rehman UU, Mahmood T (2022) The generalized dice similarity measures for bipolar complex fuzzy set and its applications to pattern recognition and medical diagnosis. Comput Appl Math 41(6):265

    MathSciNet  MATH  Google Scholar 

  • Riaz M, Tehrim ST (2019) Bipolar fuzzy soft mappings with application to bipolar disorders. Int J Biomath 12(07):1950080

    MathSciNet  MATH  Google Scholar 

  • Riaz M, Riaz M, Jamil N, Zararsiz Z (2022) Distance and similarity measures for bipolar fuzzy soft sets with application to pharmaceutical logistics and supply chain management. J Intell Fuzzy Syst (Preprint), 1–20

  • Saad M, Rafiq A (2022) Novel similarity measures for t-spherical fuzzy sets and their applications in pattern recognition and clustering. J Intell Fuzzy Syst (Preprint): 1–11

  • Shen X, Sakhi S, Ullah K, Abid MN, Jin Y (2022) Information measures based on T-spherical fuzzy sets and their applications in decision making and pattern recognition. Axioms 11(7):302

    Google Scholar 

  • Tamir DE, Jin L, Kandel A (2011) A new interpretation of complex membership grade. Int J Intell Syst 26(4):285–312

    MATH  Google Scholar 

  • Thirunavukarasu P, Suresh R, Ashokkumar V (2017) Theory of complex fuzzy soft set and its applications. Int J Innov Res Sci Technol 3(10):13–18

    Google Scholar 

  • Tripathy BK, Sooraj TR, Mohanty RK (2016) A new approach to fuzzy soft set theory and its application in decision making. In: Computational intelligence in data mining—vol. 2. Springer, New Delhi, pp 305–313

  • Ullah K (2021) Picture fuzzy Maclaurin symmetric mean operators and their applications in solving multiattribute decision-making problems. Math Probl Eng 2021. Article ID 1098631

  • Wei G, Alsaadi FE, Hayat T, Alsaedi A (2018) Bipolar fuzzy Hamacher aggregation operators in multiple attribute decision making. Int J Fuzzy Syst 20(1):1–12

    MathSciNet  MATH  Google Scholar 

  • Ye J (2011) Cosine similarity measures for intuitionistic fuzzy sets and their applications. Math Comput Model 53(1–2):91–97

    MathSciNet  MATH  Google Scholar 

  • Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353

    MATH  Google Scholar 

  • Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning—I. Inf Sci 8(3):199–249

    MathSciNet  MATH  Google Scholar 

  • Zhang WR (1994) Bipolar fuzzy sets and relations: a computational framework for cognitive modeling and multi-agent decision analysis. In: NAFIPS/IFIS/NASA'94. Proceedings of the first international joint conference of the north american fuzzy information processing society biannual conference. The Industrial Fuzzy Control and Intelligent IEEE, pp 305–309

Download references

Funding

The authors have not disclosed any funding.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, International Islamic University Islamabad, Islamabad, Pakistan

    Tahir Mahmood, Abdul Jaleel & Ubaid Ur Rehman

Authors
  1. Tahir Mahmood
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Abdul Jaleel
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ubaid Ur Rehman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Abdul Jaleel.

Ethics declarations

Conflict of interest

About the publication of this manuscript, the authors declare that they have no conflict of interest.

Ethics statement

The authors state that this is their original work and it is neither submitted nor under consideration in any other journal simultaneously.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mahmood, T., Jaleel, A. & Rehman, U.U. Pattern recognition and medical diagnosis based on trigonometric similarity measures for bipolar complex fuzzy soft sets. Soft Comput 27, 11125–11154 (2023). https://doi.org/10.1007/s00500-023-08176-y

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-023-08176-y

Keywords

Search

Navigation