Skip to main content
SpringerLink
Log in

Computational Algorithm for MRLW equation using B-spline with BFRK scheme

  • Application of soft computing
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

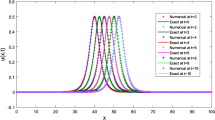
In this paper, septic B-spline approach with linearization and without linearization technique with the help of Butcher’s fifth-order Runge–Kutta scheme is implemented to obtain solitary wave solutions of the modified regularized long wave equation. The error norms \({L}_{2}\) and \({L}_{\infty }\) and the three invariants \({I}_{1}\), \({I}_{2}\) and \({I}_{3}\) are computed on three tests to confirm about the efficiency and accuracy of the proposed methods. The stability analysis is performed using Von-Neumann technique on the linearized septic B-spline approach. The results of the present work are compared with the analytical and existing solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data availability

The datasets supporting the results of this article are included within this article.

References

  • Alharbi AR, Al-Munawarah AM, Arabia S (2020) Numerical investigation for the GRLW equation using parabolic monge ampere equation, computer. Science 15:443–462

    MathSciNet  Google Scholar 

  • Bhowmik SK, Karakoc SBG (2019) Numerical approximation of the generalized regularized long wave equation using Petrov-Galerkin finite element method. Numer Methods Partial Diff Eq 35(6):2236–2257

    MathSciNet  MATH  Google Scholar 

  • Dağ İ, Irk D, Sarı M (2013) The extended cubic B-spline algorithm for a modified regularized long wave equation. Chin Phys B 22(4):040207

    Google Scholar 

  • Dash RB, Jena SR (2008) A mixed quadrature of modified Birkhoff-Young using Richardson extrapolation and Gauss-Legendre-4 point transformed rule. Int J Appl Math Appl 2:111–117

    Google Scholar 

  • Dash RB, Jena SR (2009) Multidimensional integral of several real variables. Bull Pure Appl Sci 28(1):147–154

    Google Scholar 

  • Dash P, Jena SR (2015) Mixed quadrature over sphere. Global J Pure Appl Math 11(1):415–425

    Google Scholar 

  • Essa YMA, Abouefarag I, Rahmo ED (2014) The numerical solution of the MRLW equation using the multigrid method. Appl Math 5(21):3328–3334

    Google Scholar 

  • Fazal-i-Haq, Siraj-ul-Islam, Tirmizi IA (2010) A numerical technique for solution of the MRLW equation using quartic B-splines, Appl Math Model. 34(12), 4151–4160.

  • Gardner LRT, Gardner GA, Ayoub FA, Amein NK (1997) Approximations of solitary waves of the MRLW equation by B-spline finite elements. Arab J Sci Eng 22:183–193

    MathSciNet  MATH  Google Scholar 

  • Gebremedhin GS, Jena SR (2019) Approximate solution of ordinary differential equation via hybrid block approach. Int J Emerg Technol 10(4):201–211

    Google Scholar 

  • Gebremedhin GS, Jena SR (2020) Approximate solution of a fourth order ordinary differential equation via tenth step block method. Int J Comput Sci Math 11(3):253–262

    MathSciNet  MATH  Google Scholar 

  • Guo PF, Zhang LW, Liew KM (2014) Numerical analysis of generalized regularized long wave equation using the element-free kp-Ritz method. Appl Math Comput 240:91–101

    MathSciNet  MATH  Google Scholar 

  • Hammad DA, El-Azab MS (2016) Chebyshev-Chebyshev spectral collocation method for solving the generalized regularized long wave (GRLW) equation. Appl Math Comput 285:228–240

    MathSciNet  MATH  Google Scholar 

  • Hassan HN (2017) An efficient numerical method for the modified regularized long wave equation using Fourier spectral method. J Assoc Arab Univ Basic Appl Sci 24:198–205

    Google Scholar 

  • Hossain MJ, Alam MS, Hossain MB (2017) A study on numerical solutions of second order initial value problems (IVP) for ordinary differential equations with fourth order and Butcher’s fifth order Runge-Kutta methods. Am J Comput Appl Math 7(5):129–137

    Google Scholar 

  • İnan B, Bahadir AR (2015) Numerical solutions of MRLW equation by a fully implicit finite-difference scheme. J Math Comput Sci 15:228–239

    Google Scholar 

  • Jena SR, Dash RB (2009) Mixed quadrature of real definite integral over triangles. Pacific Asian J Math 3(2):119–124

    Google Scholar 

  • Jena SR, Dash P (2015a) An efficient quadrature rule for approximate solution of non linear integral equation of Hammerstein type. Int J Appl Eng Res 10(3):5831–5840

    Google Scholar 

  • Jena SR, Dash P (2015b) Numerical treatment of analytic functions via mixed quadrature rule. Res J Appl Sci Eng Technol 10(4):391–392

    Google Scholar 

  • Jena SR, Gebremedhin GS (2020) Approximate solution of a fifth order ordinary differential equation with block method. Int J Comput Sci Math 12(4):413–426

    MathSciNet  Google Scholar 

  • Jena SR, Gebremedhin GS (2021b) Computational technique for heat and advection–diffusion equations. Soft Comput 25(16):11139–11150

    MATH  Google Scholar 

  • Jena SR, Gebremedhin GS (2022) Octic B-spline collocation scheme for numerical investigation of Fffth order boundary value problems. Int J Appl Comput Math 8(5):1–19

    MATH  Google Scholar 

  • Jena SR, Mishra SC (2015) Mixed quadrature for analytic functions. Global J Pure Appl Math. 1:281–285

    Google Scholar 

  • Jena SR, Mohanty M (2019) Numerical treatment of ODE (Fifth order). Int J Emerg Technol 10(4):191–196

    Google Scholar 

  • Jena SR, Nayak D (2019) A comparative study of numerical integration based on mixed quadrature rule and Haar wavelets. Bull Pure Appl Sci Math Stat 38(2):532–539

    Google Scholar 

  • Jena SR, Nayak D (2020) Approximate instantaneous current in RLC circuit. Bull Elect Eng Inform 9(2):803–809

    Google Scholar 

  • Jena SR, Singh A (2015) A reliable treatment of analytic functions. Int J Appl Eng Res 10(5):11691–11695

    Google Scholar 

  • Jena SR, Singh A (2018) Approximation of real definite integration. Int J Adv Res Eng Technol 9(4):197–207

    Google Scholar 

  • Jena SR, Singh A (2019) Mathematical model for approximate solution of line integral. J Comput Math Sci 10(5):1163–1172

    Google Scholar 

  • Jena SR, Meher K, Paul AK (2016) Approximation of analytic functions in adaptive environment. Beni-Suef Univ J Basic Appl Sci 5(4):306–309

    Google Scholar 

  • Jena SR, Nayak D, Acharya MM (2017) Application of mixed quadrature rule on electromagnetic field problems. Comput Math Model 28(2):267–277

    MathSciNet  Google Scholar 

  • Jena SR, Mohanty M, Mishra SK (2018) Ninth step block method for numerical solution of fourth order ordinary differential equation. Adv Model Anal A 55(2):45–56

    Google Scholar 

  • Jena SR, Senapati A, Gebremedhin GS (2020a) Approximate solution of MRLW equation in B-spline environment. Math Sci 14(3):345–357

    MathSciNet  MATH  Google Scholar 

  • Jena SR, Senapati A, Gebremedhin GS (2020b) Numerical study of solitions in BFRK scheme. Int J Mech Control 21(2):163–175

    Google Scholar 

  • Jena SR, Nayak D, Paul AK, Mishra SC (2020c) Mixed anti-Newtonian-Gaussian rule for real definite integrals. Adv Math: Sci J 9(11):1081–1090

    Google Scholar 

  • Jena SR, Sahoo M, Mohanty PK, Misra SK, Mishra BB (2022a) Application and convergence analysis of mixed quadrature rule for approximate solution of product integral. Math Eng, Sci Aerospace 13(4):1119–1129

    Google Scholar 

  • Jena SR, Rout PK, Mohanty PK, Misra SK, Paul AK (2022b) Adaptive quadrature on Line Integral in engineering. Math Eng, Sci Aerospace 13(4):1109–1118

    Google Scholar 

  • Jena SR, Acharya MM, Paul AK, Mishra BB, Rout PK, Singh A (2022c) Numerical treatment and comparative study for Fredholm Integral equation of second kind. Math Eng, Sci Aerosp 13(2):511–520

    Google Scholar 

  • Jena SR, Gebremedhin GS (2021a), Decatic B-spline collocation scheme for approximate solution of Burgers’ equation, Numer Methods Partial Differ Eq. https://doi.org/10.1002/num.22747.

  • Jena SR, Nayak D (2015) Hybrid quadrature for numerical treatment of nonlinear Fredholm integral equation with separable kernel. Int J Appl Math Stat. 53(4):83–89

    MathSciNet  MATH  Google Scholar 

  • Karakoc SBG, Yagmurlu NM, Ucar Y (2013) Numerical approximation to a solution of the modified regularized long wave equation using quintic B-splines. Bound Value Prob 1:1–17

    MathSciNet  MATH  Google Scholar 

  • Karakoc SBG, Ucar Y, Yagmurlu NM (2015) Numerical solutions of the MRLW equation by cubic B-spline Galerkin finite element method. Kuwait J Sci 42:141–159

    MathSciNet  MATH  Google Scholar 

  • Karakoç SBG, Zeybek H (2016) Solitary-wave solutions of the GRLW equation using septic B-spline collocation method. Appl Math Comput 289:159–171

    MathSciNet  MATH  Google Scholar 

  • Karakoç SBG, Ak T, Zeybek H (2014) An efficient approach to numerical study of the MRLW equation with B-Spline collocation method. Abstr Appl Anal 2014:1–15

    MathSciNet  MATH  Google Scholar 

  • Kaya D (2004) A numerical simulation of solitary-wave solutions of the generalized regularized long-wave equation. Appl Math Comput 149(3):833–841

    MathSciNet  MATH  Google Scholar 

  • Khalifa AK, Raslan KR, Alzubaidi HM (2007) A finite difference scheme for the MRLW and solitary wave interactions. Appl Math Comput 189(1):346–354

    MathSciNet  MATH  Google Scholar 

  • Khalifa AK, Raslan KR, Alzubaidi HM (2008a) A collocation method with cubic B-splines for solving the MRLW equation. J Comput Appl Math 212(2):406–418

    MathSciNet  MATH  Google Scholar 

  • Khalifa AK, Raslan KR, Alzubaidi HM (2008b) Numerical study using ADM for the modified regularized long wave equation. Appl Math Model 32(12):2962–2972

    MathSciNet  MATH  Google Scholar 

  • Korpinar Z, Tchier F, Inc M, Ragoubd L, Bayram M (2019) New soliton solutions of the fractional regularized long wave burger equation by means of conformable derivative. ResultsinPhysics 14:1–7

    Google Scholar 

  • Meher K, Jena SR, Paul AK (2017) Approximate solution of real definite integrals in adaptive routine. Indian J Sci Technol 10(5):1–4

    Google Scholar 

  • Mishra SC, Jena SR (2018) Approximate evaluation of analytic function through extrapolation. Int J Pure Appl Math 118(3):791–800

    Google Scholar 

  • Mohammadi R (2015) Exponential B-spline collocation method for numerical solution of the generalized regularized long wave equation. Chin Phys B 24(5):050206

    Google Scholar 

  • Mohammadi M, Mokhtari R (2011) Solving the generalized regularized long wave equation on the basis of a reproducing kernel space. J Comput Appl Math 235(14):4003–4014

    MathSciNet  MATH  Google Scholar 

  • Mohanty M, Jena SR (2018) Differential transformation method for approximate solution of ordinary differential equation (ODE). Adv Model Anal b 61(3):135–138

    Google Scholar 

  • Mohanty PK, Hota MK, Jena SR (2014) A comparative study of mixed quadrature rule with the compound quadrature rules. Am Int J Res Sci, Technol, Eng Math 3:45–52

    Google Scholar 

  • Mohanty M, Jena SR, Misra SK (2021a) Approximate solution of fourth order differential equation. Adv Math: Sci J 10(1):621–628

    Google Scholar 

  • Mohanty M, Jena SR, Misra SK (2021b) Mathematical modelling in engineering with integral transforms via modified Adomian decomposition method. Math Model Eng Prob 8(3):409–417

    Google Scholar 

  • Nayak D, Jena SR, Acharya MM (2017) Approximate solution of Muntz system. Global J Pure Appl Math 13(7):3013–3020

    Google Scholar 

  • Ramos JI (2007) Solitary wave interactions of the GRLW equation. Chaos, Solitons Fract 33(2):479–491

    Google Scholar 

  • Raslan KR, Ali KK (2019) Adomian decomposition method (ADM) for solving the nonlinear generalized regularized long wave equation. Numer Comput Methods Sci Eng 1(1):41–55

    Google Scholar 

  • Raslan KR, EL Danaf TS (2010) Solitary waves solutions of the MRLW equation using quintic B-splines. J King Saud Univ–sci 22(3):161–166

    Google Scholar 

  • Raslan KR, Hassan SM (2009) Solitary waves for the MRLW equation. Appl Math Lett 22(7):984–989

    MathSciNet  MATH  Google Scholar 

  • Roshan T, Petrov A (2012) Galerkin method for solving the generalized regularized long wave (GRLW) equation. Comput Math Appl 63(5):943–956

    MathSciNet  MATH  Google Scholar 

  • Salih H, Tawfiq LNM, Yahya ZR, Zin SM (2018) solving modified regularized long wave equation using collocation method. IOP Conf Series: J Phys: Conf Series 1003(1):012062

    Google Scholar 

  • Senapati A, Jena SR (2022) A computational scheme for fifth order boundary value problems. Int J Inf Technol 14(3):1397–1404

    Google Scholar 

  • Singh A, Jena SR, Mishra BB (2017) Mixed quadrature rule for double integrals. Int J Pure Appl Math 117(1):1–9

    Google Scholar 

  • Soliman AMA (2017) Collocation method using quartic B-splines for solving the modified RLW equation, Indian. J Sci Technol 10:1–7

    Google Scholar 

  • Zeybek H, Karakoç SBG (2016) A numerical investigation of the GRLW equation using lumped Galerkin approach with cubic B-spline. Springerplus 5(1):1–17

    Google Scholar 

  • Zhang L (2005) A finite difference scheme for generalized regularized long-wave equation. Appl Math Comput 168(2):962–972

    MathSciNet  MATH  Google Scholar 

Download references

Funding

This study is not funded by any funding agency. (i.e., Authors have no funding agency).

Author information

Authors and Affiliations

  1. Department of Mathematics, School of Applied Sciences, KIIT Deemed to Be University, Bhubaneswar, Odisha, 751024, India

    Saumya Ranjan Jena & Guesh Simretab Gebremedhin

Authors
  1. Saumya Ranjan Jena
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guesh Simretab Gebremedhin
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors equally contributed to the study of conception and design. Material preparation, data collection and analysis were performed by both authors. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Saumya Ranjan Jena.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Informed consent

Informed consent was obtained from all individual participants included in the study.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jena, S.R., Gebremedhin, G.S. Computational Algorithm for MRLW equation using B-spline with BFRK scheme. Soft Comput 27, 11715–11730 (2023). https://doi.org/10.1007/s00500-023-07849-y

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-023-07849-y

Keywords

Search

Navigation