Covering soft rough sets and its topological properties with application

Abstract

In this article, we introduce the notion of the complementary soft neighborhood and present three kinds of covering soft rough set ($\mathcal {CSR}$) models. The basic properties of these models are investigated. The relationships among these models are also discussed. Moreover, we establish the topological approach to $\mathcal {CSR}$ say, $\varDelta$-topological spaces (i.e., $\varDelta$-TS). Hence, the topological properties for $\varDelta$-TS models such as $\varDelta$-open sets, $\varDelta$-closed sets, $\varDelta$-interior, $\varDelta$-closure, $\varDelta$-boundary, $\varDelta$-neighborhood and $\varDelta$-limit point are studied and the relationships between them are given. Finally, we make use of an algorithm for these proposed models to deal with uncertainties for solving the MGDM problems using the constructed topologies.

1 Introduction

The concept of rough set theory (briefly, RST) was launched by Pawlak in 1982 (Pawlak 1982, 1985) as a tool for representing and computing information in data tables. The fuzzy rough set theory (briefly, FRS) was introduced by Dubois and Prade (1990) as a combination between fuzzy set and rough set which offers a wide variety of techniques to analyze imprecise data and the RST. Since the uncertainty and incompleteness of knowledge are widespread phenomena in information systems, the FRS is a helpful approach to handle such situations. The first step in studying rough set theory was based on equivalence relations, but various extensions were developed to different mathematical concepts such as a binary relation, or a neighborhood system of a topological space and a covering (Atef et al. 2020; Alcantud and Zhan 2020; El Atik et al. 2021; Herawan et al. 2010; Hu et al. 2010; Huang et al. 2011; Jensen and Shen 2004; Liu and Zhu 2008; Pal and Mitra 2004; Qian et al. 2009; Yang and Li 2006; Yao 2010; Zhang et al. 2004; Sun et al. 2017; Wu and Zhang 2004; Yeung et al. 2015; Ziarko 1993; Pomykala 1987, 1988; Yao 1998; Yao and Yao 2012; Couso and Dubois 2011; Bonikowski et al. 1998; Zhu 2007; Zhu and Wang 2003, 2007, 2012; Tsang et al. 2008; Xu and Zhang 2007; Liu and Sai 2009).

In 2007, Deng et al. (2007) developed a new model for fuzzy rough set based on the concepts of both fuzzy covering and binary fuzzy conjunction and fuzzy implication in the framework of lattice theory. In 2008, Li et al. (2008) focused on studying the covering based rough set models via the fuzzy covering that are constructed by the lower and upper fuzzy rough approximation operators. In 2012, Ma (2012) defined the notion of complementary neighborhood of an element in the universal set and according to this notion and the classical neighborhood notion; she showed the equivalency of both notions to some types of covering rough sets.

Later, in 2016, Ma (2016) introduced the concepts of fuzzy $\beta$-covering and fuzzy $\beta$-neighborhood and then constructed two kinds of fuzzy covering-based rough set models. It should be noted that the concept of fuzzy covering is a special case of fuzzy $\beta$-covering. Yang and Hu (2017), Yang and Hu (2019) introduced three types of fuzzy covering based rough set models which are generalizations of Ma’s models, and also they proposed four types of fuzzy neighborhood operators based on a fuzzy $\beta$-covering using the notions fuzzy $\beta$-minimal and $\beta$-maximal descriptions. The concept of fuzzy neighborhood system of an object based on a given fuzzy covering was defined and discussed by D’eer et al. (2017).

We were in much need to the soft set theory (briefly, SST) notion considered by Molodtsov (1999) since many mathematical models cannot use the previous classical tools such as theory of fuzzy sets , theory of intuitionistic fuzzy sets and theory of rough sets because of the difficulties of some types of uncertainties. The absence of all restrictions on the approximate description in soft set theory makes this theory easily applicable in practice in different topics. A combination of fuzzy sets with soft sets made by Maji et al. (2002) initiated an important model. Several authors have applied this theory in their research (Alcantud 2020; Ali 2011; Feng et al. 2010; Li and Xie 2014; Min 2020; Zhan and Alcantud 2019; Zhan and Wang 2019).

In 2010, Feng et al. (2011) introduced soft approximation spaces, soft rough approximations and soft rough sets based on granulation structures. Later, Feng (2011) gave an application of soft rough approximation in multi-criteria group decision-making problems. Yüksel et al. (2014), Yüksel et al. (2015) established a soft covering approximation space from a covering soft set and then defined the soft minimal description of an object, and explored an application of soft covering based rough set. Li et al. (2015) investigated parameter reductions of a soft covering. Riaz et al. (2019) brought out topological structures of soft rough sets. Another extension was made by Zhan and Alcantud (2019). They introduced a soft rough covering ($\mathcal {CSR}$) by means of soft neighborhoods and then used it to improve decision making in a multi-criteria group environment. A new approach called modified soft rough set, for studying roughness through soft sets in order to find approximations of a set was done by Shabir et al. (2013).

The objective of this article is to introduce new types of soft neighborhoods and use them to construct novel models of $\mathcal {CSR}$ which are of better quality than the existence models (i.e., growing the lower approximation and lowering the upper approximation of Feng’s, Riaz’s and Zhan’s models). The relationships between them being clarified. In addition, we discuss some topological properties of the four topologies introduced based on the $\mathcal {CSR}$ approach. Finally, we explain the relationships among these kinds and establish a numerical example to solve MGDM problems. The body of this paper is implemented here. Section 2 gives basic terminologies. Section 3 describes three types of $\mathcal {CSR}$ by using the notions of soft neighborhoods and complementary soft neighborhoods. In Sect. 4, we establish the topological approach for $\mathcal {CSR}$ models and study their properties. In Sect. 5, we solve a real problem through the proposed study. We write the aim of this article in Sect. 6.

2 Preliminaries

a quick survey of the notions which will be used in the coming sections.

Definition 2.1

Yang and Hu (2019) Let $\Upsilon$ be a universe of discourse, and ${\textbf{E}}$ be a finite set of relevant parameters regarding $\Upsilon$. The pair ${\textbf{S}} = ({{\textbf{F}}}, {\textbf{A}})$ is a soft set over $\Upsilon$, when ${\textbf{A}} \subseteq {\textbf{E}}$ and ${{\textbf{F}}}: {\textbf{A}} \rightarrow {\mathscr {P}}(\Upsilon )$ (i.e., ${{\textbf{F}}}$ is a set-valued mapping from the subset of attributes ${\textbf{A}}$ to $\Upsilon$ and ${\mathscr {P}}(\Upsilon )$ denotes the set of all subsets of $\Upsilon$).

Definition 2.2

Feng et al. (2010); Min (2020) The soft set ${\textbf{S}} = ({{\textbf{F}}}, {\textbf{A}})$ is called a full soft set if $\bigcup _{g\in {\textbf{A}}}{{\textbf{F}}}(g)=\Upsilon$ and a full soft set ${\textbf{S}} = ({{\textbf{F}}}, {\textbf{A}})$ is called a soft covering (briefly, ${{\mathcal {S}}}{{\mathcal {C}}}$) over $\Upsilon$ if for each $g \in {\textbf{A}}$, then ${{\textbf{F}}}(g)\ne \emptyset .$ In addition, $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ is called a soft covering approximation space ($\mathcal {SCAS}$ for short).

Definition 2.3

Feng (2011) Let $(\Upsilon ,{\textbf{S}})$ be a soft approximation space. For each ${L} \subseteq \Upsilon$, define the Feng-lower and Feng-upper approximations, respectively, as follows.

$$\begin{aligned}{} & {} {\mathscr {F}}^{\ominus }({L})=\{g \in \Upsilon : \exists \nu \in {\textbf{A}} \ni g \in {{\textbf{F}}}(\nu )\subseteq {L}\}, \\{} & {} {\mathscr {F}}^{\oplus }({L})=\{g \in \Upsilon : \exists \nu \in {\textbf{A}} \ni g \in {{\textbf{F}}}(\nu )\cap {L} \ne \emptyset \}. \end{aligned}$$

If ${\mathscr {F}}^{\ominus }({L}) \ne {\mathscr {F}}^{\oplus }({L})$, then L is called Feng-approximation soft rough sets($\mathcal {F-ASR}$ for short), otherwise it is definable.

In Shabir et al. (2013), Shabir et al. introduced the concept of modified soft rough sets ($\mathcal {MSR}$-sets for short) as follows.

Definition 2.4

Shabir et al. (2013) Let $(\Upsilon ,{\textbf{S}})$ be a soft approximation space. For each ${L} \subseteq \Upsilon$, define the function $\delta : \Upsilon \rightarrow {\mathscr {P}}({\textbf{A}})$ by $\delta (g)=\{\nu \in {\textbf{A}}:g\in {{\textbf{F}}}(\nu ) \}, \forall g \in \Upsilon$. Thus the Shabir-lower and Shabir-upper approximations are defined, respectively, as follows.

$$\begin{aligned} {\mathscr {S}}^{\ominus }({L})= & {} \{g \in {L}: \ni \delta (g)\ne \delta (h), \forall h \in {L}^{c} \}, \\ \ \ {\mathscr {S}}^{\oplus }({L})= & {} \{g \in {L}: \ni \delta (g)= \delta (h), \forall h \in {L} \}. \end{aligned}$$

If ${\mathscr {S}}^{\ominus }({L}) \ne {\mathscr {S}}^{\oplus }({L})$, then L is called Shabir-approximation modified soft rough sets ($\mathcal {S-AMSR}$ for short), otherwise it is definable.

Definition 2.5

Yüksel et al. (2014, 2015) Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. For each $g \in \Upsilon$, define a soft minimal description of g as follows.

$$\begin{aligned}{} & {} {\mathscr {X}}_{5}(g)=\{{{\textbf{F}}}(h):h \in {\textbf{A}}, g \in {{\textbf{F}}}(h) \wedge (\forall \nu \in {\textbf{A}},\\{} & {} \quad g \in {{\textbf{F}}}(\nu ) \subseteq {{\textbf{F}}}(h) \implies {{\textbf{F}}}(\nu ) = {{\textbf{F}}}(h))\}. \end{aligned}$$

Definition 2.6

Yüksel et al. (2014, 2015) Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. For each ${L} \subseteq \Upsilon$, define the 1(2)-Yüksel-lower and 1(2)-Yüksel-upper approximations, respectively, as follows.

$$\begin{aligned}{} & {} {\mathscr {Y}}^{\ominus }_{1}({L})\\{} & {} \quad =\cup _{\nu \in {\textbf{A}}}\{{{\textbf{F}}}(\nu ):{{\textbf{F}}}(\nu )\subseteq {L}\}, \ \ {\mathscr {Y}}^{\oplus }_{1}({L})\\{} & {} \quad =\cup \{{\mathscr {X}}_{5}(g):g\in {L}\}.\\{} & {} \qquad {\mathscr {Y}}^{\ominus }_{2}({L})=\cup _{\nu \in {\textbf{A}}}\{{{\textbf{F}}}(\nu ):{{\textbf{F}}}(\nu )\subseteq {L}\}, \ \ {\mathscr {Y}}^{\oplus }_{2}({L})\\{} & {} \quad ={\mathscr {Y}}^{\ominus }_{2}({L})\cup \{{\mathscr {X}}_{5}(g):g\in {L}-{\mathscr {Y}}^{\ominus }_{2}({L})\}. \end{aligned}$$

If ${\mathscr {Y}}^{\ominus }_{1}({L})$(${\mathscr {Y}}^{\ominus }_{2}({L})$) $\ne {\mathscr {S}}^{\oplus }({L})$ (${\mathscr {Y}}^{\oplus }_{2}({L})$), then L is called 1(2)-Yüksel-covering modified soft rough sets ($1-\mathcal {Y-CMSR}$ and $2-\mathcal {Y-CMSR}$ for short), otherwise it is definable.

Definition 2.7

Li et al. (2015) Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. For each ${L} \subseteq \Upsilon$, define the Li-lower and Li-upper approximations, respectively, as follows.

$$\begin{aligned} {\mathscr {L}}^{\ominus }({L})= & {} \cup _{\nu \in {\textbf{A}}}\{{{\textbf{F}}}(\nu ):{{\textbf{F}}}(\nu )\subseteq {L}\}, \ \ \nonumber \\ {\mathscr {L}}^{\oplus }({L})= & {} \cup _{\nu \in {\textbf{A}}}\{{{\textbf{F}}}(\nu ):{L} \cap {{\textbf{F}}}(\nu ) \ne \emptyset \}. \end{aligned}$$

If ${\mathscr {L}}^{\ominus }({L}) \ne {\mathscr {L}}^{\oplus }({L})$, then L is called Li-covering soft rough sets ($\mathcal {L-CSR}$ for short), otherwise it is definable.

Definition 2.8

Zhan and Alcantud (2019) Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. For each $g \in \Upsilon$, define a soft neighborhood of g as follows.

$$\begin{aligned} {\mathscr {X}}_{1}(g)=\bigcap \{{{\textbf{F}}}(h): h \in {\textbf{A}}, g \in {{\textbf{F}}}(h)\}. \end{aligned}$$

Definition 2.9

Zhan and Alcantud (2019) Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. For each ${L} \subseteq \Upsilon$, define the Zhan-lower and Zhan-upper approximations, respectively, as follows.

$$\begin{aligned}{} & {} {\hat{P}}_{-1}({L})=\bigg \{h \in \Upsilon : {\mathscr {X}}_{1}(h)\subseteq {L} \bigg \},\ \\{} & {} {\hat{P}}_{+1}({L})=\bigg \{h \in \Upsilon : {\mathscr {X}}_{1}(h)\cap {L} \ne \emptyset \bigg \}. \end{aligned}$$

If ${\hat{P}}_{-1}({L}) \ne {\hat{P}}_{+1}({L})$, then L is called Zhan-covering soft rough sets ($\mathcal {CSR}^{1}$ for short), otherwise it is definable.

3 Covering soft rough sets

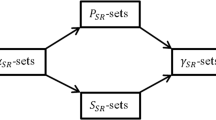
The aim of this section is to extent the idea of Zhan’s method given in [61]. This will be done via the complementary soft neighborhood. Also, we generalize it using two known neighborhoods through combining between Zhan’s and complementary neighborhoods. Thus three new kinds of $\mathcal {CSR}$ are investigated. The relevant characteristics are also discussed.

Definition 3.1

Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. For each $g \in \Upsilon$, define three kinds of the soft neighborhood of g as follows.

$$\begin{aligned} {\mathscr {X}}_{2}(g)= \{h \in \Upsilon , g \in {\mathscr {X}}_{1}(h)\}. \\ {\mathscr {X}}_{3}(g)={\mathscr {X}}_{1}(g)\cap {\mathscr {X}}_{2}(g). \end{aligned}$$

$$\begin{aligned} {\mathscr {X}}_{4}(g)={\mathscr {X}}_{1}(g)\cup {\mathscr {X}}_{2}(g). \end{aligned}$$

Example 3.2

Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$ and $({{\textbf{F}}},{\textbf{A}})$ be a soft set given as listed in Table 1.

Table 1 Table for $({{\textbf{F}}},{\textbf{A}})$

Compute the four types of soft neighborhoods as the following.

${\mathscr {X}}_{1}(g_1)=\{g_1,g_2\}, {\mathscr {X}}_{1}(g_2)=\{g_1,g_2\}, {\mathscr {X}}_{1}(g_3)=\{g_3\}, {\mathscr {X}}_{1}(g_4)=\{g_4,g_5\}, {\mathscr {X}}_{1}(g_5)=\{g_5\},$

${\mathscr {X}}_{2}(g_1)=\{g_1,g_2\}, {\mathscr {X}}_{2}(g_2)=\{g_1,g_2\}, {\mathscr {X}}_{2}(g_3)=\{g_3\}, {\mathscr {X}}_{2}(g_4)=\{g_4\}, {\mathscr {X}}_{2}(g_5)=\{g_4,g_5\},$

${\mathscr {X}}_{3}(g_1)=\{g_1,g_2\}, {\mathscr {X}}_{3}(g_2)=\{g_1,g_2\}, {\mathscr {X}}_{3}(g_3)=\{g_3\}, {\mathscr {X}}_{3}(g_4)=\{g_4\}, {\mathscr {X}}_{3}(g_5)=\{g_5\},$ and

${\mathscr {X}}_{4}(g_1)=\{g_1,g_2\}, {\mathscr {X}}_{4}(g_2)=\{g_1,g_2\}, {\mathscr {X}}_{4}(g_3)=\{g_3\}, {\mathscr {X}}_{4}(g_4)=\{g_4,g_5\}, {\mathscr {X}}_{4}(g_5)=\{g_4,g_5\}.$

Definition 3.3

Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. For each ${L} \subseteq \Upsilon$, define three kinds of lower (${\hat{P}}_{-2}, {\hat{P}}_{-3}$ and ${\hat{P}}_{-4}$) and corresponding upper (${\hat{P}}_{+2}, {\hat{P}}_{+3}$ and ${\hat{P}}_{+4}$) approximation, respectively, as follows.

$$\begin{aligned} {\hat{P}}_{-2}({L})=\bigg \{h \in \Upsilon : {\mathscr {X}}_{2}(h)\subseteq {L} \bigg \},\ \\ {\hat{P}}_{+2}({L})=\bigg \{h \in \Upsilon : {\mathscr {X}}_{2}(h)\cap {L} \ne \emptyset \bigg \}. \\ {\hat{P}}_{-3}({L})=\bigg \{h \in \Upsilon : {\mathscr {X}}_{3}(h)\subseteq {L} \bigg \},\ \\ {\hat{P}}_{+3}({L})=\bigg \{h \in \Upsilon : {\mathscr {X}}_{3}(h)\cap {L} \ne \emptyset \bigg \}. \\ {\hat{P}}_{-4}({L})=\bigg \{h \in \Upsilon : {\mathscr {X}}_{4}(h)\subseteq {L} \bigg \},\ \\ {\hat{P}}_{+4}({L})=\bigg \{h \in \Upsilon : {\mathscr {X}}_{4}(h)\cap {L} \ne \emptyset \bigg \}. \end{aligned}$$

If ${\hat{P}}_{-2}({L})$ (resp., ${\hat{P}}_{-3}({L}), {\hat{P}}_{-4}({L})$)$\ne {\hat{P}}_{+2}({L})$ (resp., ${\hat{P}}_{+3}({L}), {\hat{P}}_{+4}({L})$), then L is called a covering soft rough ($\mathcal {CSR}^{2}$, $\mathcal {CSR}^{3}$, and $\mathcal {CSR}^{4}$), otherwise it is definable.

Example 3.4

Consider again Example 3.2. Calculate $\mathcal {CSR}^{1}, \mathcal {CSR}^{2}, \mathcal {CSR}^{3}$, and $\mathcal {CSR}^{4}$ for ${L}=\{g_1,g_3,g_5\}$ as follows.

$$\begin{aligned}{} & {} {\hat{P}}_{-1}({L})=\{g_3,g_5\}, \\{} & {} {\hat{P}}_{+1}({L})=\Upsilon ,\ \ {\hat{P}}_{-2}({L})=\{g_3\}, \\{} & {} {\hat{P}}_{+2}({L})=\{g_1,g_2,g_3,g_5\}\\{} & {} {\hat{P}}_{-3}({L})=\{g_3,g_5\}, \\{} & {} {\hat{P}}_{+3}({L})=\{g_1,g_2,g_3,g_5\}, \\{} & {} {\hat{P}}_{-4}({L})=\{g_3\}, \ \ {\hat{P}}_{+4}({L})=\Upsilon \end{aligned}$$

In the following, we can obtain the accuracy measure for the four types of covering soft rough sets in Definitions 2.9 and 3.3 as follows.

Definition 3.5

Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. For each ${L} \subseteq \Upsilon$, define four types of accuracy measures $Acc_{k}$, forall $k \in \{1,2,3,4\}$ as follows.

• (1) ${Acc}_{1}({L})=\frac{|{\hat{P}}_{-1}({L})|}{|{\hat{P}}_{+1}({L})|}$.

• (2) ${Acc}_{2}({L})=\frac{|{\hat{P}}_{-2}({L})|}{|{\hat{P}}_{+2}({L})|}$.

• (3) ${Acc}_{3}({L})=\frac{|{\hat{P}}_{-3}({L})|}{|{\hat{P}}_{+3}({L})|}$.

• (4) ${Acc}_{4}({L})=\frac{|{\hat{P}}_{-4}({L})|}{|{\hat{P}}_{+4}({L})|}$, Where |L| represents the cardinal numbers of L.

The following example shows the differences between these types of measures.

Example 3.6

Consider again Example 3.4. Calculate the accuracy measures as follows.

$$\begin{aligned}{} & {} {Acc}_{1}({L})=\frac{2}{5}, {Acc}_{2}({L})=\frac{1}{4},\\{} & {} {Acc}_{3}({L}) =\frac{1}{2}, {Acc}_{4}({L})=\frac{1}{5}. \end{aligned}$$

From the above example, it is easy to see that $\mathcal {CSR}^{3}$ is more accurate than the others.

The following two Theorems 3.7 and 3.8 for $\mathcal {CSR}^{2}$, $\mathcal {CSR}^{3}$, and $\mathcal {CSR}^{4}$ hold. We prove them in the case of $\mathcal {CSR}^{2}$ only and the others are similar.

Theorem 3.7

Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. If ${L}_{1}, {L}_{2} \subseteq \Upsilon$, then we have the following relations hold.

• (1) ${\hat{P}}_{-2}(\emptyset )=\emptyset , {\hat{P}}_{-2}(\Upsilon )=\Upsilon .$

• (2) ${\hat{P}}_{-2}({L}) \subseteq {L}.$

• (3) ${\hat{P}}_{-2}({L}^{c})=\big ({\hat{P}}_{+2}({L})\big )^{c}.$

• (4) If ${L}_{1} \subseteq {L}_{2}$, then ${\hat{P}}_{-2}({L}_{1}) \subseteq {\hat{P}}_{-2}({L}_{2}).$

• (5) ${\hat{P}}_{-2}({\hat{P}}_{-2}({L}))={\hat{P}}_{-2}({L}).$

• (6) ${\hat{P}}_{-2}({L}_{1}\cap {L}_{2})={\hat{P}}_{-2}({L}_{1}) \cap {\hat{P}}_{-2}({L}_{2}).$

• (7) ${\hat{P}}_{-2}({L}_{1}) \cup {\hat{P}}_{-2}({L}_{2}) \subseteq {\hat{P}}_{-2}({L}_{1}\cup {L}_{2}).$

Proof

• (1) ${\hat{P}}_{-2}(\emptyset )=\big \{h \in \Upsilon : {\mathscr {X}}_{2}(h)\subseteq \emptyset \big \}=\emptyset .$

• (2) ${\hat{P}}_{-2}(\Upsilon )=\big \{h \in \Upsilon : {\mathscr {X}}_{2}(h)\subseteq \Upsilon \big \}=\Upsilon .$

• (3) ${\hat{P}}_{-2}({L}^{c})=\big \{h \in \Upsilon : {\mathscr {X}}_{2}(h)\subseteq {L}^{c} \big \}=\big \{h \in \Upsilon : {\mathscr {X}}_{2}(h)\subseteq {L}^{c} \big \}=\big \{h \in \Upsilon : {\mathscr {X}}_{2}(h)\cap {L} \ne \emptyset \big \}^{c}=\big ({\hat{P}}_{+2}({L})\big )^{c}.$

• (4) ${\hat{P}}_{-2}({L}_{1})=\big \{h \in \Upsilon : {\mathscr {X}}_{2}(h)\subseteq {L}_{1} \big \}\subseteq \big \{h \in \Upsilon : {\mathscr {X}}_{2}(h)\subseteq {L}_{2} \big \}={\hat{P}}_{-2}({L}_{2}).$

• (5) If $g \in {\hat{P}}_{-2}({L}) \implies {\mathscr {X}}_{2}(g)\subseteq {L}, \text {by (4)} \implies {\hat{P}}_{-2}({\mathscr {X}}_{2}(g)) \subseteq {\hat{P}}_{-2}({L}).$ Let $h \in {\mathscr {X}}_{2}(g) \implies {\mathscr {X}}_{2}(h) \subseteq {\mathscr {X}}_{2}(g) \implies h \in {\hat{P}}_{-2}({\mathscr {X}}_{2}(g)) \implies {\mathscr {X}}_{2}(g) \subseteq {\hat{P}}_{-2}({\mathscr {X}}_{2}(g)) \subseteq {\hat{P}}_{-2}({L}) \implies g \in {\hat{P}}_{-2}({\hat{P}}_{-2}({L})) \implies {\hat{P}}_{-2}({L}) \subseteq {\hat{P}}_{-2}({\hat{P}}_{-2}({L})).$

  As ${\hat{P}}_{-2}({L}) \subseteq {L}$, by (2), ${\hat{P}}_{-2}({\hat{P}}_{-2}({L})) \subseteq {\hat{P}}_{-2}({L}).$ Therefore, ${\hat{P}}_{-2}({\hat{P}}_{-2}({L})) = {\hat{P}}_{-2}({L})$.

• (6) ${\hat{P}}_{-2}({L}_{1}\cap {L}_{2})=\big \{h \in \Upsilon : {\mathscr {X}}_{2}(h)\subseteq ({L}_{1} \cap {L}_{2}) \big \}=\big \{h \in \Upsilon : {\mathscr {X}}_{2}(h)\subseteq {L}_{1} \wedge {\mathscr {X}}_{2}(h)\subseteq {L}_{2} \big \}=\big \{h \in \Upsilon : {\mathscr {X}}_{2}(h)\subseteq {L}_{1} \big \}\wedge \big \{h \in \Upsilon : {\mathscr {X}}_{2}(h)\subseteq {L}_{2} \big \}={\hat{P}}_{-2}({L}_{1}) \cap {\hat{P}}_{-2}({L}_{2}).$

• (7) Since ${L}_{1} \subseteq {L}_{1} \cup {L}_{2}$, then by (5), we have ${\hat{P}}_{-2}({L}_{1})\subseteq {\hat{P}}_{-2}({L}_{1}\cup {L}_{2})$. Also, ${L}_{2} \subseteq {L}_{1} \cup {L}_{2}$, by (5) we have ${\hat{P}}_{-2}({L}_{2}) \subseteq {\hat{P}}_{-2}({L}_{1}\cup {L}_{2})$. Thus ${\hat{P}}_{-2}({L}_{1}) \cup {\hat{P}}_{-2}({L}_{2}) \subseteq {\hat{P}}_{-2}({L}_{1}\cup {L}_{2}).$

$\square$

Theorem 3.8

Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. If ${L}_{1}, {L}_{2} \subseteq \Upsilon$, then we have the following relations hold.

• (1) ${\hat{P}}_{+2}(\emptyset )=\emptyset , {\hat{P}}_{+2}(\Upsilon )=\Upsilon .$

• (2) ${L} \subseteq {\hat{P}}_{+2}({L}).$

• (3) ${\hat{P}}_{+2}({L}^{c})=\big ({\hat{P}}_{-2}({L})\big )^{c}.$

• (4) ${\hat{P}}_{+2}({\hat{P}}_{+2}({L}))={\hat{P}}_{+2}({L}).$

• (5) If ${L}_{1} \subseteq {L}_{2}$, then ${\hat{P}}_{+2}({L}_{1}) \subseteq {\hat{P}}_{+2}({L}_{2}).$

• (6) ${\hat{P}}_{+2}({L}_{1}\cap {L}_{2})\subseteq {\hat{P}}_{+2}({L}_{1}) \cap {\hat{P}}_{+2}({L}_{2}).$

• (7) ${\hat{P}}_{+2}({L}_{1}\cup {L}_{2})={\hat{P}}_{+2}({L}_{1}) \cup {\hat{P}}_{+2}({L}_{2}).$

Proof

The proof is similar to Theorem 3.7. $\square$

Definition 3.9

Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. For each ${L} \subseteq \Upsilon$, define the positive, negative and boundary region for the three kinds $\mathcal {CSR}$ of L as follows.

$$\begin{aligned}{} & {} {\mathcal {O}}^{\oplus }_{k}({L})={\hat{P}}_{-k}({L}),\\{} & {} {\mathcal {O}}^{\ominus }_{k}({L}) =\Upsilon -{\hat{P}}_{+k}({L}),\\{} & {} {\mathscr {B}}_{k}({L})={\hat{P}}_{+k}({L})-{\hat{P}}_{-k}({L}). \end{aligned}$$

Example 3.10

Consider Example 3.4. If ${L}=\{g_1,g_3,g_5\}$, then we obtain the following outcomes.

$$\begin{aligned} {\mathcal {O}}^{\oplus }_{1}({L})= & {} {\hat{P}}_{-1}({L})=\{g_3,g_5\},\\ \ \ {\mathcal {O}}^{\ominus }_{1}({L})= & {} \Upsilon -{\hat{P}}_{+1}({L})=\emptyset ,\\ \ \ {\mathscr {B}}_{1}({L})= & {} {\hat{P}}_{+1}({L})-{\hat{P}}_{-1}({L})=\{g_1,g_2,g_4\},\\ {\mathcal {O}}^{\oplus }_{2}({L})= & {} {\hat{P}}_{-2}({L})=\{g_3\}, \ \ \\ {\mathcal {O}}^{\ominus }_{2}({L})= & {} \Upsilon -{\hat{P}}_{+2}({L})=\{g_4\},\\ \ \ {\mathscr {B}}_{2}({L})= & {} {\hat{P}}_{+2}({L})-{\hat{P}}_{-2}({L})=\{g_1,g_2,g_5\},\\ {\mathcal {O}}^{\oplus }_{3}({L})= & {} {\hat{P}}_{-3}({L})=\{g_3,g_5\}, \ \ \\ {\mathcal {O}}^{\ominus }_{3}({L})= & {} \Upsilon -{\hat{P}}_{+3}({L})=\{g_4\}, \ \ \\ {\mathscr {B}}_{3}({L})= & {} {\hat{P}}_{+3}({L})-{\hat{P}}_{-3}({L})=\{g_1,g_2\} \end{aligned}$$

and

$$\begin{aligned} {\mathcal {O}}^{\oplus }_{4}({L})= & {} {\hat{P}}_{-4}({L})=\{g_3\}, \ \ \\ {\mathcal {O}}^{\ominus }_{4}({L})= & {} \Upsilon -{\hat{P}}_{+4}({L})=\emptyset , \ \ \\ {\mathscr {B}}_{4}({L})= & {} {\hat{P}}_{+4}({L})-{\hat{P}}_{-4}({L})=\{g_1,g_2,g_4,g_5\} \end{aligned}$$

The next remark explains the comparisons between the given approximations by using the boundary region.

Remark 3.11

The goal of approximations is to reduce the boundary zone as possible to get a reliable solution. Here, by the above Example 3.10, ${\mathscr {B}}_{3}({L})$ is least than the others (i.e., ${\mathscr {B}}_{1}({L})$, ${\mathscr {B}}_{2}({L})$ and ${\mathscr {B}}_{4}({L})$) . This means that $\mathcal {CSR}^{3}$ is more accurate than the others.

Next, we present new kind of a degree of soft rough membership as follows.

Definition 3.12

Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. For each ${L} \subseteq \Upsilon$, define three new kinds of a degree of soft rough membership of L as follows.

$$\begin{aligned}{} & {} {{\mathbb {D}}}_{2}(h,{L})=\frac{|{L} \cap {\mathscr {X}}_{2}(h)|}{|{\mathscr {X}}_{2}(h)|}, (\forall h \in \Upsilon ),\\{} & {} \quad {{\mathbb {D}}}_{3}(h,{L})=\frac{|{L} \cap {\mathscr {X}}_{3}(h)|}{|{\mathscr {X}}_{3}(h)|}, (\forall h \in \Upsilon ), \end{aligned}$$

and

$$\begin{aligned} {{\mathbb {D}}}_{4}(h,{L})=\frac{|{L} \cap {\mathscr {X}}_{4}(h)|}{|{\mathscr {X}}_{4}(h)|}, (\forall h \in \Upsilon ). \end{aligned}$$

Example 3.13

Consider Example 3.2. If ${L}=\{g_1,g_3,g_5\}$, then we get the following values.

$$\begin{aligned}{} & {} {{\mathbb {D}}}_{1}(g_1,{L})=\frac{1}{2},\ \ {{\mathbb {D}}}_{2}(g_1,{L})=\frac{1}{2} ,\ \\{} & {} \quad {{\mathbb {D}}}_{3}(g_1,{L})=\frac{1}{2} ,\ \ {{\mathbb {D}}}_{4}(g_1,{L})=\frac{1}{2}.\\{} & {} \quad {{\mathbb {D}}}_{1}(g_2,{L})=\frac{1}{2},\ \ {{\mathbb {D}}}_{2}(g_2,{L})=\frac{1}{2} ,\ \\{} & {} \quad {{\mathbb {D}}}_{3}(g_2,{L})=\frac{1}{2} ,\ \ {{\mathbb {D}}}_{4}(g_2,{L})=\frac{1}{2}.\\{} & {} \quad {{\mathbb {D}}}_{1}(g_3,{L})=1,\ \ {{\mathbb {D}}}_{2}(g_3,{L})=1 ,\ \\{} & {} \quad {{\mathbb {D}}}_{3}(g_3,{L})=1 ,\ \ {{\mathbb {D}}}_{4}(g_3,{L})=1.\\{} & {} \quad {{\mathbb {D}}}_{1}(g_4,{L})=\frac{1}{2},\ \ {{\mathbb {D}}}_{2}(g_4,{L})=0 ,\ \\{} & {} \quad {{\mathbb {D}}}_{3}(g_4,{L})=0 ,\ \ {{\mathbb {D}}}_{4}(g_4,{L})=\frac{1}{2}.\\{} & {} \quad {{\mathbb {D}}}_{1}(g_5,{L})=1,\ \ {{\mathbb {D}}}_{2}(g_5,{L})=\frac{1}{2} ,\ \\{} & {} \quad {{\mathbb {D}}}_{3}(g_5,{L})=1 ,\ \ {{\mathbb {D}}}_{4}(g_5,{L})=\frac{1}{2}. \end{aligned}$$

The next two Theorems 3.14 and 3.15 are true for ${{\mathbb {D}}}_{2}(h,{L})$, ${{\mathbb {D}}}_{3}(h,{L})$, and ${{\mathbb {D}}}_{4}(h,{L})$. We prove them for ${{\mathbb {D}}}_{2}(h,{L})$ only and for the other cases the proofs are similar.

Theorem 3.14

Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. If $L \subseteq \Upsilon$ and $h \in \Upsilon$, then we have the following characteristics.

• (1) ${{\mathbb {D}}}_{2}(h,{L})=1 \iff h \in {\hat{P}}_{-2}({L}).$

• (2) ${{\mathbb {D}}}_{2}(h,{L})=0 \iff h \in \Upsilon -{\hat{P}}_{+2}({L}).$

• (3) $0<{{\mathbb {D}}}_{2}(h,{L})<1 \iff h \in {\hat{P}}_{+2}({L})-{\hat{P}}_{-2}({L}).$

Proof

• (1) ${{\mathbb {D}}}_{2}(h,{L})=1 \iff {\mathscr {X}}_{2}(h) \subseteq {L} \iff h \in {\hat{P}}_{-2}({L}).$

• (2) ${{\mathbb {D}}}_{2}(h,{L})=0 \iff {\mathscr {X}}_{2}(h) \cap {L}=\emptyset \iff h \notin {\hat{P}}_{+2}({L}) \iff h \in \Upsilon -{\hat{P}}_{+2}({L}).$

• (3) It is clear by Definition 3.12.

$\square$

Theorem 3.15

Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. If ${L} \subseteq \Upsilon$ and $h \in \Upsilon$, then we have the following items.

• (1) If ${L}_{1} \subseteq {L}_{2}$, then ${{\mathbb {D}}}_{2}(h,{L}_{1}) {L}eq {{\mathbb {D}}}_{2}(h,{L}_{2}).$

• (2) ${{\mathbb {D}}}_{2}(h,{L}_{1} \cup {L}_{2})\ge {{\mathbb {D}}}_{2}(h,{L}_{1}) \vee {{\mathbb {D}}}_{2}(h,{L}_{2})$.

• (3) If ${L}_{1} \subseteq {L}_{2}$ or ${L}_{2} \subseteq {L}_{1}$, then ${{\mathbb {D}}}_{2}(h,{L}_{1} \cup {L}_{2})= {{\mathbb {D}}}_{2}(h,{L}_{1}) \vee {{\mathbb {D}}}_{2}(h,{L}_{2})$.

• (4) ${{\mathbb {D}}}_{2}(h,{L}_{1} \cap {L}_{2}){L}eq {{\mathbb {D}}}_{2}(h,{L}_{1}) \wedge {{\mathbb {D}}}_{2}(h,{L}_{2})$.

• (5) If ${L}_{1} \subseteq {L}_{2}$ or ${L}_{2} \subseteq {L}_{1}$, then ${{\mathbb {D}}}_{2}(h,{L}_{1} \cap {L}_{2})= {{\mathbb {D}}}_{2}(h,{L}_{1}) \wedge {{\mathbb {D}}}_{2}(h,{L}_{2})$.

• (6) ${{\mathbb {D}}}_{2}(h,{L})+{{\mathbb {D}}}_{2}(h,{L}^{c})=1.$

Proof

• (1) Suppose that ${L}_{1} \subseteq {L}_{2}$ and $h \in \Upsilon$. Then $|{L}_{1} \cap {\mathscr {X}}_{2}(h)| {L}eq |{L}_{2} \cap {\mathscr {X}}_{2}(h)|$, and hence $\frac{|{L}_{1} \cap {\mathscr {X}}_{2}(h)|}{|{\mathscr {X}}_{2}(h)|} \le \frac{|{L}_{2} \cap {\mathscr {X}}_{2}(h)|}{|{\mathscr {X}}_{2}(h)|}$, i.e., ${{\mathbb {D}}}_{2}(h,{L}_{1}) \le {{\mathbb {D}}}_{2}(h,{L}_{2}).$

• (2) If ${L}_{1} \subseteq {L}_{2}$, then we obtain ${{\mathbb {D}}}_{2}(h,{L}_{1} \cup {L}_{2})=\frac{|({L}_{1}\cup {L}_{2}) \cap {\mathscr {X}}_{2}(h)|}{|{\mathscr {X}}_{2}(h)|}=\frac{|({L}_{1}\cap {\mathscr {X}}_{2}(h))\cup ({L}_{2} \cap {\mathscr {X}}_{2}(h))|}{|{\mathscr {X}}_{2}(h)|} \ge \frac{\bigvee \big [|{L}_{1} \cap {\mathscr {X}}_{2}(h)|,|{L}_{2} \cap {\mathscr {X}}_{2}(h)|\big ]}{|{\mathscr {X}}_{2}(h)|} =\bigvee \bigg [\frac{|{L}_{1} \cap {\mathscr {X}}_{2}(h)|}{|{\mathscr {X}}_{2}(h)|}, \frac{|{L}_{2} \cap {\mathscr {X}}_{2}(h)|}{|{\mathscr {X}}_{2}(h)|} \bigg ]=\bigvee \big [{{\mathbb {D}}}_{2}(h,{L}_{1}), {{\mathbb {D}}}_{2}(h,{L}_{2})\big ] ={{\mathbb {D}}}_{2}(h,{L}_{1}) \vee {{\mathbb {D}}}_{2}(h,{L}_{2}).$

• (3), (4) and (5) Straightforward by (2).

• (6) ${{\mathbb {D}}}_{2}(h,{L})+{{\mathbb {D}}}_{2}(h,{L}^{c})=\frac{|{L} \cap {\mathscr {X}}_{2}(h)|}{|{\mathscr {X}}_{2}(h)|}+\frac{|{L}^{c} \cap {\mathscr {X}}_{2}(h)|}{|{\mathscr {X}}_{2}(h)|}=\frac{|{L}_{1} \cap {\mathscr {X}}_{2}(h)|+|{L}^{c} \cap {\mathscr {X}}_{2}(h)|}{|{\mathscr {X}}_{2}(h)|}=\frac{|{\mathscr {X}}_{2}(h)|}{|{\mathscr {X}}_{2}(h)|}=1.$

$\square$

Example 3.16

Consider Example 3.2. If ${L}_{1}=\{g_1\}$ and ${L}_{2}=\{g_2\}$, then we get the following values.

• (1) ${{\mathbb {D}}}_{2}(g_1,{L}_{1})=\frac{1}{2}, \ \ {{\mathbb {D}}}_{2}(g_1,{L}_{2})=\frac{1}{2}, \ \ {{\mathbb {D}}}_{2}(g_1,{L}_{1} \cup {L}_{2})=1$ but ${{\mathbb {D}}}_{2}(g_1,{L}_{1}) \vee {{\mathbb {D}}}_{2}(g_1,{L}_{2})=\frac{1}{2}$. Hence, ${{\mathbb {D}}}_{2}(g_{1},{L}_{1} \cup {L}_{2})\ngeq {{\mathbb {D}}}_{2}(g_{1},{L}_{1}) \vee {{\mathbb {D}}}_{2}(g_{1},{L}_{2}).$

• (2) ${L}_{1} \cap {L}_{2}=\emptyset$, then we have ${{\mathbb {D}}}_{2}(g_{2},{L}_{1}) \wedge {{\mathbb {D}}}_{2}(g_{2},{L}_{2})=\frac{1}{2}$ and ${{\mathbb {D}}}_{2}(g_{2},{L}_{1} \cap {L}_{2})=0$. Thus, ${{\mathbb {D}}}_{2}(g_{2},{L}_{1} \cap {L}_{2})\nleq {{\mathbb {D}}}_{2}(g_{2},{L}_{1}) \wedge {{\mathbb {D}}}_{2}(g_{2},{L}_{2}).$

Next, let us show the relationship between the different $\mathcal {CSR}$ models. These are clarified by the following propositions.

Proposition 3.17

Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. If ${L} \subseteq \Upsilon$ and $h \in \Upsilon$, then we have the following characteristics.

• (1) ${\hat{P}}_{-4}({L}) \subseteq {\hat{P}}_{-2}({L}) \subseteq {\hat{P}}_{-3}({L}).$

• (2) ${\hat{P}}_{-4}({L}) \subseteq {\hat{P}}_{-1}({L}) \subseteq {\hat{P}}_{-3}({L}).$

• (3) ${\hat{P}}_{+3}({L}) \subseteq {\hat{P}}_{+2}({L}) \subseteq {\hat{P}}_{+4}({L}).$

• (4) ${\hat{P}}_{+3}({L}) \subseteq {\hat{P}}_{+1}({L}) \subseteq {\hat{P}}_{+4}({L}).$

Proof

Obvious. $\square$

Proposition 3.18

Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$. If ${L} \subseteq \Upsilon$ and $h \in \Upsilon$, then we have the following characteristics.

• (1) ${\hat{P}}_{-3}({L}) = {\hat{P}}_{-1}({L}) \cup {\hat{P}}_{-2}({L}).$

• (2) ${\hat{P}}_{-4}({L}) = {\hat{P}}_{-1}({L}) \cap {\hat{P}}_{-2}({L}).$

• (3) ${\hat{P}}_{+3}({L}) = {\hat{P}}_{+1}({L}) \cap {\hat{P}}_{+2}({L}).$

• (4) ${\hat{P}}_{+4}({L}) = {\hat{P}}_{+1}({L}) \cup {\hat{P}}_{+2}({L}).$

Proof

Obvious. $\square$

4 Topological approach to $\mathcal {CSR}$

This section deals with all the definitions of four types of topologies come from $\mathcal {CSR}$ models called $\varDelta -{{\mathcal {T}}}{{\mathcal {S}}}$ and explored their relevant properties.

Definition 4.1

Let $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$ be an $\mathcal {SCAS}$ of $\Upsilon$. For each $g \in \Upsilon$, define four kinds of topologies as follow.

$$\begin{aligned} {\mathscr {T}}_{1}=\{{\mathcal {E}} \subseteq \Upsilon : {\mathscr {X}}_{1}(g) \subseteq {\mathcal {E}}\} \\ {\mathscr {T}}_{2}=\{{\mathcal {E}} \subseteq \Upsilon : {\mathscr {X}}_{2}(g) \subseteq {\mathcal {E}}\} \\ {\mathscr {T}}_{3}=\{{\mathcal {E}} \subseteq \Upsilon : {\mathscr {X}}_{3}(g) \subseteq {\mathcal {E}}\} \\ {\mathscr {T}}_{4}=\{{\mathcal {E}} \subseteq \Upsilon : {\mathscr {X}}_{4}(g) \subseteq {\mathcal {E}}\}, \end{aligned}$$

each of which satisfies the topological conditions as for each $\varDelta = \{i\}, i \in \{1,2,3,4\}$. For $i=1$, $\varDelta =\{1\}.$

• (1) It is obvious that $\Upsilon$ and $\emptyset$ are in ${\mathscr {T}}_{1}$.

• (2) Assume that $\{{L}_{l} : l \in I\}$ be in ${\mathscr {T}}_{1}$ and let $g \in \cup {L}_{l}$. Then $\exists$ $l_1 \in l$ and $g \in {L}_{1}$ such that ${\mathscr {X}}_{1}(g) \subseteq {L}_{1}$ $\implies$ ${\mathscr {X}}_{1}(g) \subseteq \cup {L}_{l}$. Thus $\cup {L}_{l} \in {\mathscr {T}}_{1}$.

• (3) Consider ${L}_{1}, {L}_{2} \in {\mathscr {T}}_{1}$ and $g \in {L}_{1} \cap {L}_{2}$, thus $g \in {L}_{1}$ and $g \in {L}_{2}$. So, ${\mathscr {X}}_{1}(g) \subseteq {L}_{1}$ and ${\mathscr {X}}_{1}(g) \subseteq {L}_{2}$. Hence, ${\mathscr {X}}_{1}(g) \subseteq {L}_{1} \cap {L}_{2}$. Therefore ${L}_{1} \cap {L}_{2} \in {\mathscr {T}}_{1}.$

  From the above relations, ${\mathscr {T}}_{\varDelta }({L})$ is called $\varDelta$-topology, then $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ is called $\varDelta$-topological space ($\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$).

Now, let us show in details these topologies when we consider Example 4.2.

Example 4.2

Consider Example 3.2, then the four topologies are listed below. The steps for calculating the first type of topology is as follows.

• (1) The subbase is $\{\{g_1,g_2\},\{g_3\},\{g_4,g_5\},\{g_5\}\}$,

• (2) The base is a finite intersection of the members of the subbase as $\{\{g_1,g_2\},\{g_3\},\{g_4,g_5\},\{g_5\},\emptyset \}$,

• (3) Topology is the arbitrary union of the members of the base as

  ${\mathscr {T}}_{1}=\{\Upsilon ,\emptyset ,\{g_3\}, \{g_5\}, \{g_1,g_2\}, \{g_3,g_5\}, \{g_4,g_5\},$ $\{g_1,g_2,g_3\},\{g_1,g_2,g_5\},\{g_3,g_4,g_5\}, \{g_1,g_2,g_3,g_5\},$ $\{g_1,g_2,g_4,g_5\} \},$

  In the same manner, we can compute the other three kinds as next.

  ${\mathscr {T}}_{2}=\{\Upsilon ,\emptyset ,\{g_3\}, \{g_4\}, \{g_1,g_2\}, \{g_3,g_4\}, \{g_4,g_5\},$ $\{g_1,g_2,g_3\},\{g_1,g_2,g_4\},\{g_3,g_4,g_5\},$ $\{g_1,g_2,g_3,g_4\},\{g_1,g_2,g_4,g_5\} \},$

  ${\mathscr {T}}_{3}=\{\Upsilon ,\emptyset ,\{g_3\},\{g_4\},\{g_5\},\{g_1,g_2\}, \{g_3,g_4\}, \{g_3,g_5\},$ $\{g_4,g_5\}, \{g_1,g_2,g_3\},\{g_1,g_2,g_4\}, \{g_1,g_2,g_5\},$ $\{g_3,g_4,g_5\}, \{g_1,g_2,g_3,g_4\},\{g_1,g_2,g_3,g_5\},$ $\{g_1,g_2,g_4,g_5\} \}$ and

  ${\mathscr {T}}_{4}=\{\Upsilon ,\emptyset ,\{g_3\},\{g_1,g_2\}, \{g_4,g_5\},$ $\{g_1,g_2,g_3\},\{g_3,g_4,g_5\}, \{g_1,g_2,g_4,g_5\} \}.$

Definition 4.3

Let $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ be a $\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$. Define the $\varDelta$-closed sets as follows.

$$\begin{aligned} {\textbf{C}}_{\varDelta }=\{{\mathbb {F}} \subseteq \Upsilon : {\mathbb {F}}^{c} \in {\mathscr {T}}_{\varDelta } \}. \end{aligned}$$

Definition 4.4

Let $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ be a $\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$. Define the $\varDelta$-interior and $\varDelta$-closure of ${L} \subseteq \Upsilon$, respectively, as follows.

$$\begin{aligned} \Im ^{\varDelta }({L})= & {} \cup \{{{\mathbb {D}}}\in {\mathscr {T}}_{\varDelta }: {{\mathbb {D}}}\subseteq {L}\} \text {and} \ \\\ C^{\varDelta }({L})= & {} \cap \{{{{\mathcal {W}}}}\in {\textbf{C}}_{\varDelta }: {L} \subseteq {{{\mathcal {W}}}}\}. \end{aligned}$$

Example 4.5

Consider Example 3.2. If ${L}=\{g_1,g_3,g_5\}$, then we have

• (1) $\Im ^{1}({L})=\{g_3,g_5\},\ \ {{\mathbb {C}}}^{1}({L})=\Upsilon .$

• (2) $\Im ^{2}({L})=\{g_3\},\ \ {{\mathbb {C}}}^{2}({L})=\{g_1,g_2,g_3,g_5\}.$

• (3) $\Im ^{3}({L})=\{g_3,g_5\},\ \ {{\mathbb {C}}}^{3}({L})=\{g_1,g_2,g_3,g_5\}.$

• (4) $\Im ^{4}({L})=\{g_3\},\ \ {{\mathbb {C}}}^{4}({L})=\Upsilon .$

Corollary 4.6

Let $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ be a $\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$. Then we have the following equalities hold.

• (1) ${\hat{P}}_{-1}({L})=\Im ^{1}({L}), \ \ {\hat{P}}_{+1}({L})={{\mathbb {C}}}^{1}({L}).$

• (2) ${\hat{P}}_{-2}({L})=\Im ^{2}({L}), \ \ {\hat{P}}_{+2}({L})={{\mathbb {C}}}^{2}({L}).$

• (3) ${\hat{P}}_{-3}({L})=\Im ^{3}({L}), \ \ {\hat{P}}_{+3}({L})={{\mathbb {C}}}^{3}({L}).$

• (4) ${\hat{P}}_{-4}({L})=\Im ^{4}({L}), \ \ {\hat{P}}_{+4}({L})={{\mathbb {C}}}^{4}({L}).$

Theorem 4.7

Let $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ be a $\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$. For each ${L},{L}_{1},{L}_{2} \subseteq \Upsilon$, the following relations are correct.

• (1) $\Im ^{\varDelta }(\emptyset )=\emptyset , \Im ^{\varDelta }(\Upsilon )=\Upsilon .$

• (2) $\Im ^{\varDelta }({L}) \subseteq {L}.$

• (3) L is open set $\iff \$ $\Im ^{\varDelta }({L}) = {L}.$

• (4) $\Im ^{\varDelta }(\Im ^{\varDelta }({L}))=\Im ^{\varDelta }({L}).$

• (5) If ${L}_{1} \subseteq {L}_{2}$, then $\Im ^{\varDelta }({L}_{1}) \subseteq \Im ^{\varDelta }({L}_{2}).$

• (6) $\Im ^{\varDelta }({L}_{1}\cap {L}_{2})=\Im ^{\varDelta }({L}_{1}) \cap \Im ^{\varDelta }({L}_{2}).$

• (7) $\Im ^{\varDelta }({L}_{1}) \cup \Im ^{\varDelta }({L}_{2}) \subseteq \Im ^{\varDelta }({L}_{1}\cup {L}_{2}).$

Proof

We shall prove only the theorem when $\varDelta =\{1\}$. The other cases are similar.

• (1) $\Im ^{1}(\emptyset )=\cup \{{{\mathbb {D}}}\in {\mathscr {T}}_{1}: {{\mathbb {D}}}\subseteq \emptyset \}=\emptyset , \ \ \Im ^{1}(\Upsilon )=\cup \{{{\mathbb {D}}}\in {\mathscr {T}}_{1}: {{\mathbb {D}}}\subseteq \Upsilon \}=\Upsilon .$

• (2) This is clear by Definition 4.4.

• (3) If L is open set, then the largest open set that is contained in L is L itself. Hence, $\Im ^{\varDelta }({L}) = {L}.$

  On the other hand, let $\Im ^{\varDelta }({L}) = {L}$. As $\Im ^{\varDelta }({L})$ is $\varDelta$-open set, L is $\varDelta$-open set.

• (4) $\Im ^{1}(\Im ^{1}({L}))=\cup \{{{\mathbb {D}}}\in {\mathscr {T}}_{1}: {{\mathbb {D}}}\subseteq \Im ^{1}({L})\}=\cup \{{{\mathbb {D}}}\in {\mathscr {T}}_{1}: {{\mathbb {D}}}\subseteq \cup \big [{{\mathbb {D}}}\in {\mathscr {T}}_{1}: {{\mathbb {D}}}\subseteq {L}\big ]\}=\cup \{{{\mathbb {D}}}\in {\mathscr {T}}_{1}: {{\mathbb {D}}}\subseteq {L}\}=\Im ^{1}({L}).$

• (5) $\Im ^{1}({L}_{1})=\cup \{{{\mathbb {D}}}\in {\mathscr {T}}_{1}: {{\mathbb {D}}}\subseteq {L}_{1}\} \subseteq \cup \{{{\mathbb {D}}}\in {\mathscr {T}}_{1}: {{\mathbb {D}}}\subseteq {L}_{2}\}=\Im ^{1}({L}_{2}).$

• (6) $\Im ^{\varDelta }({L}_{1}\cap {L}_{2})=\cup \{{{\mathbb {D}}}\in {\mathscr {T}}_{1}: {{\mathbb {D}}}\subseteq ({L}_{1}\cap {L}_{2})\}=\cup \{{{\mathbb {D}}}\in {\mathscr {T}}_{1}: {{\mathbb {D}}}\subseteq {L}_{1} \wedge {{\mathbb {D}}}\subseteq {L}_{2}\}=\cup \{{{\mathbb {D}}}\in {\mathscr {T}}_{1}: {{\mathbb {D}}}\subseteq {L}_{1}\}\wedge \cup \{{{\mathbb {D}}}\in {\mathscr {T}}_{1}: {{\mathbb {D}}}\subseteq {L}_{2}\}=\Im ^{\varDelta }({L}_{1}) \cap \Im ^{\varDelta }({L}_{2}).$

• (7) Since ${L}_{1} \subseteq {L}_{1} \cup {L}_{2}$, by (5) we have $\Im ^{\varDelta }({L}_{1})\subseteq \Im ^{\varDelta }({L}_{1}\cup {L}_{2})$. Also, ${L}_{2} \subseteq {L}_{1} \cup {L}_{2}$, implies that by (5), $\Im ^{\varDelta }({L}_{2})\subseteq \Im ^{\varDelta }({L}_{1}\cup {L}_{2})$. Thus $\Im ^{\varDelta }({L}_{1}) \cup \Im ^{\varDelta }({L}_{2}) \subseteq \Im ^{\varDelta }({L}_{1}\cup {L}_{2}).$

$\square$

Theorem 4.8

Let $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ be a $\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$. For each ${L},{L}_{1},{L}_{2} \subseteq \Upsilon$. Then the following relations hold.

• (1) ${{\mathbb {C}}}^{\varDelta }(\emptyset )=\emptyset , {{\mathbb {C}}}^{\varDelta }(\Upsilon )=\Upsilon .$

• (2) ${{\mathbb {C}}}^{\varDelta }({L}) \subseteq {L}.$

• (3) L is $\varDelta$-closed set $\iff \$ ${{\mathbb {C}}}^{\varDelta }({L}) = {L}.$

• (4) ${{\mathbb {C}}}^{\varDelta }({{\mathbb {C}}}^{\varDelta }({L}))={{\mathbb {C}}}^{\varDelta }({L}).$

• (5) If ${L}_{1} \subseteq {L}_{2}$, then ${{\mathbb {C}}}^{\varDelta }({L}_{1}) \subseteq {{\mathbb {C}}}^{\varDelta }({L}_{2}).$

• (6) ${{\mathbb {C}}}^{\varDelta }({L}_{1}) \cup {{\mathbb {C}}}^{\varDelta }({L}_{2}) = {{\mathbb {C}}}^{\varDelta }({L}_{1}\cup {L}_{2}).$

• (7) ${{\mathbb {C}}}^{\varDelta }({L}_{1} \cap {L}_{2}) \subseteq {{\mathbb {C}}}^{\varDelta }({L}_{1}) \cap {{\mathbb {C}}}^{\varDelta }({L}_{2}).$

Proof

The proof is similar to the one in Theorem 4.7. $\square$

Definition 4.9

Let $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ be a $\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$. For each ${L} \subseteq \Upsilon$, define the $\varDelta$-boundary of L as follows.

$$\begin{aligned} {{{\mathcal {B}}}}^{\varDelta }({L})={{\mathbb {C}}}^{\varDelta }({L}) \cap {{\mathbb {C}}}^{\varDelta }({L}^{c}). \end{aligned}$$

Theorem 4.10

Let $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ be a $\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$. For each ${L} \subseteq \Upsilon$. Then the following equalities hold.

• (1) ${{\mathbb {C}}}^{\varDelta }({L})={L} \cup {{{\mathcal {B}}}}^{\varDelta }({L}).$

• (2) $\Im ^{\varDelta }({L})={L}-{{{\mathcal {B}}}}^{\varDelta }({L}).$

Proof

We shall only prove the theorem taking $\varDelta =\{1\}$. The other cases are almost similar.

• (1) Suppose that ${L} \subseteq \Upsilon$. Then $\Upsilon ={L} \cup {L}^{c} \subseteq {L} \cup {{\mathbb {C}}}^{1}({L}^{c}) \subseteq \Upsilon$. Thus $\Upsilon = {L} \cup {{\mathbb {C}}}^{1}({L}^{c})$. So, we have

  ${L} \cup {{{\mathcal {B}}}}^{1}({L})={L} \cup \big ({{\mathbb {C}}}^{1}({L}) \cap {{\mathbb {C}}}^{1}({L}^{c})\big ) =\big ({L} \cup {{\mathbb {C}}}^{1}({L})\big )\cap \big ({L} \cup {{\mathbb {C}}}^{1}({L}^{c})\big ) ={{\mathbb {C}}}^{1}({L}) \cap \big ({L} \cup {{\mathbb {C}}}^{1}(\upsilon -\Im ^{1}({L}))\big )= {{\mathbb {C}}}^{1}({L}) \cap \Upsilon ={{\mathbb {C}}}^{1}({L}).$

• (2) ${L}-{{{\mathcal {B}}}}^{\varDelta }({L})={L}-\big ({{\mathbb {C}}}^{1}({L}) \cap {{\mathbb {C}}}^{1}({L}^{c})\big )={L} \cap \big ({{\mathbb {C}}}^{1}({L}) \cap {{\mathbb {C}}}^{1}({L}^{c})\big )^{c}= {L} \cap \big (({{\mathbb {C}}}^{1}({L}))^{c} \cup ({{\mathbb {C}}}^{1}({L}^{c}))^{c}\big ) ={L} \cap \big (\Im ^{1}({L}^{c})\cup \Im ^{1}({L})\big )= \big ({L}\cap \Im ^{1}({L}^{c})\big )\cup \big ({L}\cap \Im ^{1}({L})\big )=\emptyset \cup \Im ^{1}({L})=\Im ^{1}({L}).$ $\square$

As a consensus of the above theorem we have the following remark.

Remark 4.11

Let $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ be a $\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$. For each ${L} \subseteq \Upsilon$, the following results hold.

• (1) L is open set $\iff \$ ${L} \cap {{{\mathcal {B}}}}^{\varDelta }({L})=\emptyset .$

• (2) L is closed set $\iff \$ ${L} \supseteq {{{\mathcal {B}}}}^{\varDelta }({L}).$

• (3) ${{{\mathcal {B}}}}^{\varDelta }({L})=\emptyset \iff$ L is $\varDelta$-open and $\varDelta$-closed set.

Definition 4.12

Let $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ be a $\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$. For each $g \in \Upsilon$ and ${L} \subseteq \Upsilon$. We say L is a $\varDelta$-neighborhood of g if $\exists {L}_{g} \in {\mathscr {T}}_{\varDelta }$ with $g \in {L}_{g} \subseteq {L}.$

Definition 4.13

Let $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ be a $\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$. For each $g \in \Upsilon$ and ${L} \subseteq \Upsilon$. We say L is a $\varDelta$-limit point of g if every $\varDelta$-open set ${{\mathbb {T}}}$ containing g, it is also contains a point of L different from g, i.e.,

$$\begin{aligned} {{\mathbb {T}}}\cap ({L}-\{g\})\ne \emptyset . \end{aligned}$$

Also, the set of all $\varDelta$-limit points of L is said to be the derived set of L and is denoted by ${L}^{{{\mathbb {D}}}}.$

It is an easy target to prove the following theorem, so we omit it.

Theorem 4.14

Let $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ be a $\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$. For each ${L} \subseteq \Upsilon$. Then the following properties holds.

• (1) ${{\mathbb {C}}}^{\varDelta }({L})={L} \cup {L}^{{{\mathbb {D}}}}.$

• (2) L is closed set $\iff \ {L} \supseteq {L}^{{{\mathbb {D}}}}.$

Next, we discuss the relationships between these different kinds of topologies as follows.

Proposition 4.15

Let $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ be a $\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$. Then for each ${L} \subseteq \Upsilon$, we have the following relations.

• (1) $\Im ^{4}({L}) \subseteq \Im ^{2}({L}) \subseteq \Im ^{3}({L}).$

• (2) $\Im ^{4}({L}) \subseteq \Im ^{1}({L}) \subseteq \Im ^{3}({L}).$

• (3) ${{\mathbb {C}}}^{3}({L}) \subseteq {{\mathbb {C}}}^{2}({L}) \subseteq {{\mathbb {C}}}^{4}({L}).$

• (4) ${{\mathbb {C}}}^{3}({L}) \subseteq {{\mathbb {C}}}^{1}({L}) \subseteq {{\mathbb {C}}}^{4}({L}).$

Proof

Follows directly from Definition 4.1. $\square$

Proposition 4.16

Let $(\Upsilon ,{\mathscr {T}}_{\varDelta }({L}),{\textbf{A}})$ be a $\varDelta$-${{\mathcal {T}}}{{\mathcal {S}}}$. Then we have the following relations.

• (1) $\Im ^{3}({L})= \Im ^{1}({L}) \cup \Im ^{2}({L}).$

• (2) ${{\mathbb {C}}}^{3}({L})= {{\mathbb {C}}}^{1}({L}) \cap {{\mathbb {C}}}^{2}({L}).$

• (3) $\Im ^{4}({L})= \Im ^{1}({L}) \cap \Im ^{2}({L}).$

• (4) ${{\mathbb {C}}}^{4}({L})= {{\mathbb {C}}}^{1}({L}) \cup {{\mathbb {C}}}^{2}({L}).$

Proof

Straightforward. $\square$

5 An application by using the proposed method

Let us presume that $\{g_1,g_2,g_3,...,g_{r}\}$ be r engineers (alternatives) and $\{\nu _{1}, \nu _{2},...,\nu _{m}\}$ be m attributes connected to a company which needs to offer a job for an engineering. Thus we use the beauty of soft set to evaluate the optimal engineer through our suggested covering method. So, we establish the MGDM with $(\Upsilon ,{{\textbf{F}}},{\textbf{A}})$, where $\Upsilon =\{g_1,g_2,g_3,...,g_{r}\}$ and ${\textbf{A}}=\{\nu _{1}, \nu _{2},...,\nu _{m}\}$. According to the presented models, we built the following algorithm to select the best.

The clarified steps in Algorithm 1 are summarized by the following numerical example.

Example 5.1

Let us consider the engineers form a set $\Upsilon =\{g_1,g_2,g_3,...,g_{40}\}$ and the given parameters are presented by the set ${\textbf{A}}=\{\nu _{1}, \nu _{2},...,\nu _{4}\}$. These parameters corresponding to the following features, respectively (experience, skills, personality and self-confidence). So, the following steps are obtained.

Step 1 Establish the ${{\mathcal {S}}}{{\mathcal {C}}}$ $({{\textbf{F}}},{\textbf{A}})$ as in Table 2.

Table 2 Table for $({{\textbf{F}}},{\textbf{A}})$

Step 2 Construct the proficient estimation ${\mathcal {P}}=({\mathcal {M}},{\textbf{P}})$ and let the output of this estimation be ${\mathscr {Y}}$. Then ${\mathcal {M}}({\textbf{P}}_{i})={\mathscr {Y}}_{i}$ $(\forall i \in \{1,2,3\})$, and Table 3 contains the data gained by the experts.

Table 3 Table for ${\mathcal {P}}=({\mathcal {M}},{\textbf{P}})$

So, we have

${\mathscr {Y}}_{1}={\mathcal {M}}({\textbf{P}}_{1})=\{g_3,g_5\}, \ {\mathscr {Y}}_{2}={\mathcal {M}}({\textbf{P}}_{2})=\{g_2,g_4\},$ and ${\mathscr {Y}}_{3}={\mathcal {M}}({\textbf{P}}_{3})=\{g_1,g_3,g_6\}.$

Step 3 Compute the lower and upper approximation for the two soft sets ${\mathcal {P}}^{\circ }=({\mathcal {M}}^{\circ },{\textbf{P}})$ and ${\mathcal {P}}^{\bullet }=({\mathcal {M}}^{\bullet },{\textbf{P}})$, where ${\mathcal {M}}^{\circ }({\textbf{P}}_{i})={\hat{P}}_{-3}({\mathscr {Y}}_{i}), \ \ {\mathcal {M}}^{\bullet }({\textbf{P}}_{i})={\hat{P}}_{+3}({\mathscr {Y}}_{i}),$ as shown in Tables 4 and 5.

Table 4 Table for ${\mathcal {P}}^{\circ }=({\mathcal {M}}^{\circ },{\textbf{P}})$

Table 5 Table for ${\mathcal {P}}^{\bullet }=({\mathcal {M}}^{\bullet },{\textbf{P}})$

${\mathscr {X}}_{1}(g_1)=\{g_1,g_5\}, {\mathscr {X}}_{1}(g_2)=\{g_2,g_4\}, {\mathscr {X}}_{1}(g_3)=\{g_3\}, {\mathscr {X}}_{1}(g_4)=\{g_2,g_4\}, {\mathscr {X}}_{1}(g_5)=\{g_5\}, {\mathscr {X}}_{1}(g_6)=\{g_3,g_6\}.$

${\mathscr {X}}_{2}(g_1)=\{g_1\}, {\mathscr {X}}_{2}(g_2)=\{g_2,g_4\}, {\mathscr {X}}_{2}(g_3)=\{g_3,g_6\},$ ${\mathscr {X}}_{2}(g_4)=\{g_2,g_4\}, {\mathscr {X}}_{2}(g_5)=\{g_1,g_5\}, {\mathscr {X}}_{2}(g_6)=\{g_6\}.$

${\mathscr {X}}_{3}(g_1)=\{g_1\}, {\mathscr {X}}_{3}(g_2)=\{g_2,g_4\}, {\mathscr {X}}_{3}(g_3)=\{g_3\},$ ${\mathscr {X}}_{3}(g_4)=\{g_2,g_4\}, {\mathscr {X}}_{3}(g_5)=\{g_5\}, {\mathscr {X}}_{3}(g_6)=\{g_6\}.$

Thus

${\mathcal {M}}^{\circ }({\textbf{P}}_{1})={\hat{P}}_{-3}({\mathscr {Y}}_{1})= {\mathcal {M}}^{\bullet }({\textbf{P}}_{1})={\hat{P}}_{+3}({\mathscr {Y}}_{1})=\{g_3,g_5\}.$

${\mathcal {M}}^{\circ }({\textbf{P}}_{2})={\hat{P}}_{-3}({\mathscr {Y}}_{2})={\mathcal {M}}^{\bullet }({\textbf{P}}_{2})={\hat{P}}_{+3}({\mathscr {Y}}_{2})=\{g_2,g_4\},$

${\mathcal {M}}^{\circ }({\textbf{P}}_{3})={\hat{P}}_{-3}({\mathscr {Y}}_{3})= {\mathcal {M}}^{\bullet }({\textbf{P}}_{3})={\hat{P}}_{+3}({\mathscr {Y}}_{3})=\{g_1,g_3,g_6\}.$

Step 4 Build the characteristic function $\xi _{{\mathscr {Y}}}$ of ${\mathscr {Y}}$ and investigate the function of ${\mathcal {P}}=({\mathcal {M}},{\textbf{P}})$ as follows.

$$\begin{aligned} \zeta _{{\mathcal {P}}}=\Upsilon \rightarrow [0,1] \implies \zeta _{{\mathcal {P}}}(g_r)=\frac{1}{3}\sum \limits _{i=1}^{3}\xi _{{\mathscr {Y}}_{i}}(g_r). \end{aligned}$$

Also, we obtain the functions for the other two soft set as follows.

$$\begin{aligned}{} & {} \zeta _{{\mathcal {P}}^{\circ }}=\Upsilon \rightarrow [0,1] \implies \zeta _{{\mathcal {P}}^{\circ }}(g_r)\\{} & {} \quad =\frac{1}{3}\sum \limits _{i=1}^{3}\xi _{{\mathcal {M}}^{\circ }({\textbf{P}}_{i})}(g_r)\ \ \text {and} \ \ \zeta _{{\mathcal {P}}^{\bullet }}\\{} & {} \quad =\Upsilon \rightarrow [0,1] \implies \zeta _{{\mathcal {P}}^{\bullet }}(g_r)\\{} & {} \quad =\frac{1}{3}\sum \limits _{i=1}^{3}\xi _{{\mathcal {M}}^{\bullet }({\textbf{P}}_{i})}(g_r). \end{aligned}$$

Hence, the following results are obtained.

$$\begin{aligned}{} & {} \zeta _{{\mathcal {P}}}(g_r)=\frac{1/3}{g_1}+\frac{1/3}{g_2}+\frac{2/3}{g_3}\\{} & {} \quad +\frac{1/3}{g_4}+\frac{1/3}{g_5}+\frac{1/3}{g_6}, \zeta _{{\mathcal {P}}^{\circ }}(g_r)\\{} & {} \qquad =\frac{1/3}{g_1}+\frac{1/3}{g_2}+\frac{2/3}{g_3}+\frac{1/3}{g_4}+\frac{1/3}{g_5}+\frac{1/3}{g_6}, \end{aligned}$$

and

$$\begin{aligned} \zeta _{{\mathcal {P}}^{\bullet }}(g_r)=\frac{1/3}{g_1}+\frac{1/3}{g_2}+\frac{2/3}{g_3}+\frac{1/3}{g_4}+\frac{1/3}{g_5}+\frac{1/3}{g_6}. \end{aligned}$$

Step 5 Assume that $({\mathscr {L}}$(Low gratification)$,{\mathscr {M}}$ (Medium gratification), and ${\mathscr {H}}$(High gratification)) be the parameter set through experts. Thus we can establish Table 6 for the soft set ${{{\mathcal {B}}}}=(\varLambda ,\S )$, where $\varLambda ({\mathscr {L}})(g_r)=\zeta _{{\mathcal {P}}^{\bullet }}(g_r), \ \ \varLambda ({\mathscr {M}})(g_r)=\zeta _{{\mathcal {P}}}(g_r), \ \ \varLambda ({\mathscr {H}})(g_r)=\zeta _{{\mathcal {P}}^{\circ }}(g_r)$ and $\S =\{{\mathscr {L}},{\mathscr {M}},{\mathscr {H}}\}$.

Table 6 Table for ${{{\mathcal {B}}}}=(\varLambda ,\S )$

Hence, the ordering of the alternatives are as follows. Let the select outcome is $\varDelta (g_r)={\mathscr {L}}(g_r)+{\mathscr {M}}(g_r)+{\mathscr {H}}(g_r).$ So, we have

$$\begin{aligned}{} & {} \varDelta (g_1)=1, \ \ \varDelta (g_2)=1, \ \ \varDelta (g_3)=2, \ \ \varDelta (g_4)=1, \ \\{} & {} \varDelta (g_5)=1, \ \ \varDelta (g_6)=1. \end{aligned}$$

Thus,

$$\begin{aligned} g_3> g_5 \approx g_6 \approx g_1 \approx g_2 \approx g_4. \end{aligned}$$

Therefore, the 3th engineering is the best among others.

Table 7 Table for scores using different approaches

5.1 Comparative analysis

The prime objective of this work is to growing the lower approximation and lowering the upper approximation of Zhan and Alcantud (2019), Feng (2011) and Riaz et al. (2019) as seen in Example 3.4. Now, we intend to clarify the rapprochement between Zhan and Alcantud (2019), Feng (2011), Riaz et al. (2019) and our’s, the sorting outcomes of these models are set in Table 7.

In view of Table 7, the optimal alternative is the same (i.e., $g_3$) among all distinct methods that are Feng’s method Feng (2011), Zhan’s method Zhan and Alcantud (2019) and Riaz’s method Riaz et al. (2019), this means that our approach is credible and effective, with vantage to our’s in increasing the lower approximation and decreasing the upper approximation which lead to decrease the boundary region as in .

6 Conclusion

The aim of the employed techniques is to grow the lower approximation and lower the upper approximation depending very strongly on property soft neighborhoods and uses them to construct models of $\mathcal {CSR}$. Also, we studied the relations between these models. Then we turned our attention to study some of the topological properties based on the $\mathcal {CSR}$ approach. Finally, we utilized the algorithm for the proposed model to deal with MGDM problems.