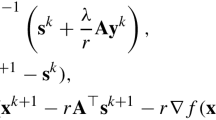Skip to main content
SpringerLink
Log in

A derivative-free memoryless BFGS hyperplane projection method for solving large-scale nonlinear monotone equations

  • Optimization
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

In this work, by combining a three-term memoryless BFGS conjugate gradient direction with the hyperplane projection technique , we develop a new derivative-free algorithm to solve nonlinear monotone equations. The method is motivated by conjugate gradient method and hyperplane projection, as well as quasi-Newton method. The search direction has three terms and is obtained by modifying the BFGS updating matrix with a unit matrix in each step. The algorithm needs no matrices computing, and it is suitable for solving large-scale nonlinear monotone equations. The proposed method satisfies the Dai–Liao conjugacy conditions and is always descent irrelative to any line searches. Under standard conditions, the optimizer solution can be obtained by a globally convergent sequence as long as the initial point is given. The reported numerical experiments show that the method is promising and efficient compared to similar algorithms in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Data availability

Enquiries about data availability should be directed to the authors.

References

  • Abubakar AB, Kumam P (2019) A descent Dai-Liao conjugate gradient method for nonlinear equations. Numer Algorithms 81:197–210

    Article  MathSciNet  MATH  Google Scholar 

  • Ahookhosh M, Amini K, Bahrami S (2013) Two derivative-free projection approaches for systems of large-scale nonlinear monotone equations. Numer Algorithms 64(1):21–42

    Article  MathSciNet  MATH  Google Scholar 

  • Aikhani Koupaei J, Firouznia M (2021) A chaos-based constrained optimization algorithm. J Ambient Intell Human Comput 12:9953–9976. https://doi.org/10.1007/s12652-020-02746-w

    Article  Google Scholar 

  • Andrei N (2010) Accelerated scaled memoryless BFGS preconditioned conjugate gradient algorithm for unconstrained optimization. Eur J Oper Res 204(3):410–420

    Article  MathSciNet  MATH  Google Scholar 

  • Andrei N (2013) A simple three-term conjugate gradient algorithm for unconstrained optimization. J Comput Appl Math 241:19–29

    Article  MathSciNet  MATH  Google Scholar 

  • Babaie-Kafaki S, Ghanbari R (2014) A descent family of Dai-Liao conjugate gradient methods. Optim Methods Softw 29(3):583–591

    Article  MathSciNet  MATH  Google Scholar 

  • Babaie-Kafaki S, Ghanbari R (2017) A class of adaptive Dai-Liao conjugate gradient methods based on the scaled memoryless BFGS update. 4OR 15(1):85–92

    Article  MathSciNet  MATH  Google Scholar 

  • Babaie-Kafaki S, Aminifard Z (2019) Two-parameter scaled memoryless BFGS methods with a nonmonotone choice for the initial step length. Numer Algorithms 82(4):1345–1357

    Article  MathSciNet  MATH  Google Scholar 

  • Cruz WL, Raydan M (2003) Nonmonotone spectral methods for large-scale nonlinear systems. Optim Methods Softw 18(5):583–599

    Article  MathSciNet  MATH  Google Scholar 

  • Dai YH, Liao LZ (2001) New conjugacy conditions and related nonlinear conjugate gradient methods. Appl Math Optim 43(1):87–101

    Article  MathSciNet  MATH  Google Scholar 

  • Dai Z, Zhu H (2020) A modified Hestenes-Stiefel-type derivative-free method for large-scale nonlinear monotone equations. Mathematics 8(2):1–14. https://doi.org/10.3390/math8020168

    Article  Google Scholar 

  • Deng S, Wan Z (2014) An improved three-term conjugate gradient algorithm for solving unconstrained optimization problems. Optimization 64(12):1–13

    MathSciNet  Google Scholar 

  • Deng S, Lv J, Wan Z (2019) A new Dai-Liao type of conjugate gradient algorithm for unconstrained optimization problems. Pacific J Optim 15(2):237–248

    MathSciNet  MATH  Google Scholar 

  • Ebrahimi A, Barid Loghmani G (2018) Shape modeling based on speci- fying the initial B-spline curve and scaled BFGS optimization method. Multimed Tools Appl 77(23):30331–30351

    Article  Google Scholar 

  • Gupta V, Mittal M (2019) QRS complex detection using STFT, Chaos analysis, and PCA in standard and real-time ECG databases. J Inst Eng India Ser B 100:489–497. https://doi.org/10.1007/s40031-019-00398-9

    Article  Google Scholar 

  • Gupta V, Mittal M, Mittal V (2020) R-peak detection based chaos analysis of ECG signal. Analog Integr Circ Sig Process 102:479–490. https://doi.org/10.1007/s10470-019-01556-1

    Article  Google Scholar 

  • Gupta V, Mittal M, Mittal V (2020) Chaos theory: an emerging tool for arrhythmia detection. Sens Imaging 21:10. https://doi.org/10.1007/s11220-020-0272-9

    Article  Google Scholar 

  • Gupta V, Mittal M, Mittal V (2021) Chaos theory and ARTFA: emerging tools for interpreting ECG signals to diagnose cardiac arrhythmias. Wirel Pers Commun 118:3615–3646. https://doi.org/10.1007/s11277-021-08411-5

    Article  Google Scholar 

  • Hager WW, Zhang H (2005) A new conjugate gradient method with guaranteed descent and an efficient line search. SIAM J Control 16:170–192

    MathSciNet  MATH  Google Scholar 

  • Li Q, Li DH (2011) A class of derivative-free methods for large-scale nonlinear monotone equations. IMA J Numer Anal 31(4):1625–1635

    Article  MathSciNet  MATH  Google Scholar 

  • Liu J, Li S (2015) A projection method for convex constrained monotone nonlinear equations with applications. Comput Math Appl 70(10):2442–2453. https://doi.org/10.1016/j.camwa.2015.09.014

    Article  MathSciNet  MATH  Google Scholar 

  • Livieris IE, Tampakas V, Pintelas P (2018) A descent hybrid conjugate gradient method based on the memoryless BFGS update. Numer Algorithms 79(4):1169–1185

    Article  MathSciNet  MATH  Google Scholar 

  • Lv J, Deng S, Wan Z (2020) An efficient single-parameter scaling memoryless Broyden-Fletcher-Goldfarb-Shanno algorithm for solving large scale unconstrained optimization problems. IEEE Access. https://doi.org/10.1109/ACCESS.2020.2992340

    Article  Google Scholar 

  • Moré JJ, Dolan ED (2002) Benchmarking optimization software with performance profiles. Math Program 91:201–213

    Article  MathSciNet  MATH  Google Scholar 

  • Nocedal J, Wright S J (1999) Numerical optimization, Spring

  • Papp Z, Rapaj S (2015) FR type methods for systems of large-scale nonlinear monotone equations. Appl Math Comput 269(C):816–823

    MathSciNet  MATH  Google Scholar 

  • Solodov MV, Svaiter BF (1998) A globally convergent inexact Newton method for systems of monotone equations. In: Fukushima M, Qi L (eds) Reformulation: Nonsmooth. Kluwer Academic Publishers, Piecewise Smooth, Semismooth and Smoothing Methods, pp 355–369

  • Xiao Y, Zhu H (2013) A conjugate gradient method to solve convex constrained monotone equations with applications in compressive sensing. J Math Anal Appl 405(1):310–319

  • Yan QR, Peng XZ, Li DH (2010) A globally convergent derivative-free method for solving large-scale nonlinear monotone equations. J Comput Appl Math 234(3):649–657

  • Zhang L, Zhou W, Li D (2006) Global convergence of a modified Fletcher-Reeves conjugate gradient method with Armijo-type line search. Numerische Mathematik 104:561–572

    Article  MathSciNet  MATH  Google Scholar 

  • Zhang L, Zhou W, Li D (2006) A descent modified Polak-Ribi\(\grave{e}\)-Polyak conjugate gradient method and its global convergence. IMA Numer Anal 26:629–640

    Article  MathSciNet  MATH  Google Scholar 

  • Zhou W, Li D (2007) Limited memory BFGS method for nonlinear monotone equations. J Comput Math 25(1):89–96

  • Zhu Q, Lin F, Li H et al (2020) Human-autonomous devices for weak signal detection method based on multimedia chaos theory. J Ambient Intell Human Comput. https://doi.org/10.1007/s12652-020-02270-x

    Article  Google Scholar 

Download references

Funding

This work is supported by National Natural Science Foundation of China (Grant Number: 51535012 and 71671190).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Central South University, Changsha, China

    Fei Huang & Songhai Deng

  2. State Key Lab High Performance Complex Mfg, Central South University, Changsha, 410083, China

    Jinyuan Tang

Authors
  1. Fei Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Songhai Deng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jinyuan Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Songhai Deng.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, F., Deng, S. & Tang, J. A derivative-free memoryless BFGS hyperplane projection method for solving large-scale nonlinear monotone equations. Soft Comput 27, 3805–3815 (2023). https://doi.org/10.1007/s00500-022-07536-4

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-022-07536-4

Keywords

Search

Navigation