Neutrosophic QUALIFLEX based on neutrosophic hesitancy index for selecting a potential antivirus mask supplier over COVID-19 pandemic

Abstract

In order to handle simultaneously the cardinal and ordinal information in decision-making process, QUALIFLEX (QUALItative FLEXible multiple criteria method) is a very well-known decision-making approach. In this work, we extend the classical QUALIFLEX method to neutrosophic environment and develop a neutrosophic QUALIFLEX (N-QUALIFLEX) method that uses the newly defined distance-based comparison approach. It is highly effective in solving multi-criteria decision problems in which both ratings of alternatives on criteria and weights of criteria are single-valued neutrosophic numbers (SVNNs), and their aggregated values are single-valued neutrosophic hesitant fuzzy numbers (SVNHFNs). A neutrosophic hesitancy index (NHI) of a SVNHN is introduced based on degrees of the truth-membership, indeterminacy-membership and falsity-membership, which is used to measure the degree of hesitancy of SVNHN. Considering the NHIS of SVNHFNs, we propose a distance-based comparison approach to determine the magnitude of the SVNHFNs. Then, we apply the comparison approach to define the concordance/discordance index, the weighted concordance/discordance index and the comprehensive concordance/discordance index that are steps of the developed N-QUALIFLEX. By taking all possible permutations of alternatives with respect to the level of concordance/discordance into account, we determine the order of alternatives in final decision. Finally, a practical example on antivirus mask selection over the COVID-19 pandemic is provided to present the effectiveness and applicability of the proposed method, and a comparative study is conducted to show the advantages of the proposed method over other existing methods.

1 Introduction

In real decision making, the decision information is usually incomplete, uncertain and vague. Thus, multi-criteria decision-making (MCDM) methods are extensively used to determine the ranking order of alternatives or to find the best solution under the appropriate criteria. The criterion values given by decision makers (DM) are generally fuzzy because of the complexity of decision problems and limitations of human thinking. In 1965, Zadeh (Zadeh 1965) presented fuzzy sets (FSs) theory to model the uncertain information. So far the applications of FSs have spread to many fields (Eftekhari et al. 2022; Mokhtia et al. 2021, 2020; Saberi-Movahed et al. 2022; Taghavi et al. 2020). FSs are expressed by a degree of membership ${T}_{A}(x)$ which indicates the degree of belonging of an element $x$ to the set $A$. To take the non-membership degree into, (Atanassov 1986) proposed an intuitionistic fuzzy set (IFS) by adding a non-membership function to FS. IFS is an extension of FSs, and it has two main functions such as the membership function ${T}_{A}(x)$ and the non-membership function ${F}_{A}(x)$. The hesitation (or indeterminacy) degree of IFS depends on the membership function ${T}_{A}(x)$ and non-membership function ${F}_{A}(x)$ and is defined by $1-{T}_{A}\left(x\right)-{F}_{A}(x)$. However, IFS can only handle incomplete information rather than indeterminate and inconsistent information and cannot solve the uncertain problems involving indeterminate and inconsistent information in real decision making. Therefore, Smarandache (Smarandache 1999) first introduced the concept of neutrosophic set (NS) by adding an independent indeterminacy-membership on the basis of IFSs. Clearly, NS is a functional tool to represent the indeterminate or inconsistent information and is a generalization of FS and IFS. In NSs, the truth-membership degree, indeterminacy-membership and falsity-membership are independently characterized. Thus, NS is more flexible and more comprehensive than FS and IFS in describing uncertain information. It is difficult to use NSs in terms of applications. Therefore, (Wang et al. 2010) proposed a single-valued neutrosophic set (SVNS), which is an instance of NS. Then, SVNSs have been extensively studied in the field of MCDM. Ye (2013) introduced the correlation coefficients and decision-making method of SVNSs. Broumi et al. (2016) introduced certain types of bipolar single-valued neutrosophic graphs, respectively. Şahin (2019) proposed an approach based on graph theory for neutrosophic information. Biswas and Pramanik (2016) extended the TOPSIS method for MCDM under a single-valued neutrosophic environment. Mokhtia et al. (2020) proposed several similarity measures between SVNSs and introduced a measure of the entropy of SVNSs. Şahin and Küçük (2015) presented a subsethood measure for SVNSs. Recently, studies on NSs rapidly have been increased in solving uncertain problems (Li et al. 2017; Majumdar and Samanta 2014; Nancy 2017; Peng et al. 2017b; Şahin and Karabacak 2015).

(Torra 2010) and (Torra 2009) presented the concept of a hesitant fuzzy set (HFS) as another extension of the FS. HFSs are very effective in the case where it is difficult to determine the membership of an element to a set and is need of giving a few different values due to doubt. However, in some situations, DMs may be asked to assign the non-membership degrees with a few different values, like the membership degrees. Zhu et al. (2012) handled this situation and introduced a dual HFS (DHFS) that has two kinds of hesitancy such as the membership hesitancy function and the non-membership hesitancy function. However, neither HFSs nor DHFSs cannot express a case where truth-membership degrees, indeterminacy-membership degrees and falsity-membership degrees for an element to a set are assigned by a few different values. To handle this case, (Ye 2014) introduced the concept of single-valued neutrosophic HFS (SVNHFS) that is a combination of HFS and SVNS, and attempted to solve a decision-making problem with three kinds of hesitancy information that exists in the real world. A SVNHFS consists of three parts such as the truth-membership hesitancy function, indeterminacy-membership hesitancy function and falsity-membership hesitancy function, and it can express easily three kinds of hesitancy information. Then, Wang and Li 2015) developed the definition of multi-valued neutrosophic set (MVNS). Actually, there is no difference between MVNSs and SVNHFSs. Moreover, both MVNSs and SVNHFSs are represented by truth-membership, indeterminacy-membership and falsity-membership functions that have a set of crisp values between zero and one. Şahin and Liu (2017) studied the correlation and correlation coefficient of SVNHFSs. Wang et al. (2010) defined the distance and similarity measures for MCDM with single-valued neutrosophic hesitant fuzzy information. Liu and Zhang (2017) defined the neutrosophic hesitant fuzzy Heronian mean aggregation operators of SVNHFSs. Biswas et al. (2016) defined some weighted distance measures of SVNHFSs and applied them to deal with practical MCDM problems. In (Li and Zhang 2018), Li and Zhang established a MCDM method based on the proposed single-valued neutrosophic hesitant fuzzy Choquet ordered averaging operator. Liu et al. (2016) proposed a series of Bonferroni mean (BM) aggregation operators for MVNSs. Peng et al. (2018a) defined a single-valued neutrosophic hesitant fuzzy geometric weighted Choquet integral Heronian mean operator. Liu and Luo 2019) introduced some aggregation operators of SVNHFS and presented their application in MCDM. Moreover, there are many special decision-making methods in the context of MVNSs. Wang and Li (2015) extend the classical TODIM method to multi-valued neutrosophic environment. Ji et al. (2018) developed a projection-based TODIM method with multi-valued neutrosophic information. Peng et al. (2018b) defined a probability multi-valued neutrosophic set and a novel qualitative flexible multiple criteria method (QUALIFLEX). Peng et al. (2017a) proposed a further multi-valued neutrosophic qualitative flexible multiple criteria method (QUALIFLEX) based on the likelihood of MVNSs to solve MCDM problems. Peng et al. (2017c) developed an extension of the ELECTRE to MVNSs. Yang and Pang (2018) presented a new multi-valued interval neutrosophic fuzzy multi-attribute decision-making method by integrating the DEMATEL and TOPSIS method. Şahin and Altun (2020) applied the MABAC method to probabilistic single-valued neutrosophic hesitant fuzzy environment. Wang (2021) proposed a MCDM method based on normalized geometric aggregation operators of SVNHFSs. Garg et al. (2022) defined the concept of complex single-valued neutrosophic hesitant fuzzy set. Özlü (2022) proposed the generalized Dice measures of single-valued neutrosophic type-2 hesitant fuzzy sets and their application to MCDM.

The QUALIFLEX (qualitative flexible multiple criteria method) developed by (Paelinck 1978) is one of the effective outranking methods to solve the MCDM problems, especially suitable to deal with the decision-making problems where the number of criteria markedly exceeds the number of alternatives. It is based on the pair-wise comparisons of alternatives with respect to each criterion under all possible alternative permutations and identifies the optimal permutation that maximizes the value of the concordance/discordance index. Recently, notably few attempts have been made to extend QUALIFLEX to the neutrosophic decision environment (Peng et al. 2018b, 2017a; Peng and Tian 2018; Tian et al. 2019). However, these methods do not take into account the degree of hesitation of the DM or decision organization. Also, they are not sufficient to solve group decision problems, in which the initial performance values of the alternatives and the weights of the criteria are single-valued neutrosophic numbers (SVNNs), and their aggregated values are single-valued neutrosophic hesitant fuzzy numbers (SVNHFNs). Therefore, in this paper, we provide some useful contributions to the process of group decision making in single-valued neutrosophic hesitant fuzzy environment. First, we define a new concept that is called the neutrosophic hesitancy index to capture the hesitancy information of SVNHFNs. Second, we propose two novel distance measures for SVNHFNs, based on their neutrosophic hesitancy indices, and moreover we introduce two comparison methods that are the distance-based and the neutrosophic hesitancy index-based for SVNHFNs. Finally, considering the distance-based comparison method, we develop a QUALIFLEX method to capture the hesitancy information of SVNHFNs and to solve MCGDM problems with neutrosophic information, in which both the performance values of alternatives and the weights of criteria are characterized by SVNHFNs. The feature of this newly developed method is that, unlike the previously developed methods, it obtains the aggregated values without using an aggregation operator that causes information loss.

This article is organized as follows. Section 2 briefly reviews some concepts of SVNS, HFSs and SVNHFS. Section 3 presents a concept of neutrosophic hesitancy index (NHI) for SVNHFNs and defines two novel distance measures as well as the novel comparison methods for SVNHFNs. Section 4 develops a novel QUALIFLEX method based on the NHI for handling the single-valued neutrosophic hesitant fuzzy information. Section 5 presents a supplier selection problem on antivirus mask selection over the COVID-19 pandemic to verify the applicability and the implementation process of the proposed method. Section 6 provides a comparative analysis with the previously developed methods. Section 7 demonstrates our conclusions and future research directions.

2 Preliminaries

In this section, the definitions and operations of NSs and SVHHFSs are introduced for using in the latter analysis.

2.1 Single-valued neutrosophic hesitant fuzzy sets (SVNHFS)

Definition 1

(Smarandache 1999) Let $X$ be a universe of discourse. $A$ neutrosophic set is defined as:

$$N=\left\{\langle x,{T}_{N}\left(x\right),{I}_{N}(x), {F}_{N}(x)\rangle :x\in X\right\},$$

(1)

which is characterized by a truth-membership function ${T}_{N}:X\to \left]{0}^{-},{1}^{+}\right[$, an indeterminacy-membership function ${I}_{N}:X\to \left]{0}^{-},{1}^{+}\right[$ and a falsity-membership function ${F}_{N}:X\to \left]{0}^{-},{1}^{+}\right[$.

There is not restriction on the sum of ${T}_{A}(x)$,${I}_{A}(x)$ and ${F}_{A}(x)$; therefore, ${0}^{-}\le \mathrm{sup}{T}_{A}\left(x\right)+\mathrm{sup}{I}_{A}\left(x\right)+\mathrm{sup}{F}_{A}(x)\le {3}^{+}.$

Definition 2

(Wang et al. 2010) Let $X$ be a universe of discourse, then a single-valued neutrosophic set (SVNS) is defined as:

$$A=\left\{\langle x,{T}_{A}\left(x\right),{I}_{A}(x), {F}_{A}(x)\rangle :x\in X\right\},$$

(2)

where ${T}_{A}:X\to [\mathrm{0,1}]$, ${I}_{A}:X\to [\mathrm{0,1}]$ and ${F}_{A}:X\to [\mathrm{0,1}]$ with $0\le T\left(x\right)+{I}_{A}\left(x\right)+{F}_{A}\left(x\right)\le 3$ for all $x\in X.$ The values ${T}_{A}(x)$,${I}_{A}(x)$ and ${F}_{A}(x)$ denote the truth-membership degree, the indeterminacy-membership degree and the falsity-membership degree of $x$ to $A,$ respectively.

In the following, we will adopt the representations ${h}_{N}(x),$ ${k}_{N}(x)$ and ${f}_{N}(x)$ instead of ${T}_{N}(x),$ ${I}_{N}(x)$ and ${F}_{N}(x)$, respectively.

Definition 3

(Taghavi et al. 2020; Torra 2009) Let $X$ be a fixed set; a hesitant fuzzy set (HFS) $M$ on X is in terms of a function that when applied to $X$ returns a subset of $[0, 1],$ which can be represented as the following mathematical symbol:

$$M=\left\{\langle x,{h}_{M}\left(x\right)\rangle :x\in X\right\},$$

(3)

where ${h}_{M}(x)$ is a set of some different values in $[\mathrm{0,1}]$ with by ${h}_{M}\left(x\right)=\left\{{\gamma }_{M1}\left(x\right),{\gamma }_{M2}\left(x\right),\dots,{\gamma }_{M{l}_{h}}\left(x\right)\right\},$ representing the possible membership degrees of the element $x\in X$ to $M$. For convenience, the ${h}_{M}(x)$ is named a hesitant fuzzy element (HFE), denoting by $h=\left\{{\gamma }_{M1},{\gamma }_{M2},\dots,{\gamma }_{M{l}_{h}}\right\},$ where ${l}_{h}$ is the number of values in ${h}_{M}(x).$

Recently, (Ye 2014) defined a single-valued neutrosophic hesitant fuzzy set (SVNHFS) as combination of the SVNS and HFS as follows:

Definition 4

(Ye 2014) Let $X$ be a fixed set, then a single-valued neutrosophic hesitant fuzzy set (SVNHFS) $N$ on $X$ is defined as,

$$N=\left\{\langle x,\left(h\left(x\right),k\left(x\right),f\left(x\right)\right)\rangle :x\in X\right\},$$

(4)

in which $h\left(x\right),k(x)$ and $f(x)$ are three sets of some different values in $[\mathrm{0,1}],$ denoting the possible truth-membership hesitant degrees, indeterminacy-membership hesitant degrees and falsity-membership hesitant degrees of the element $x\in X$ to $N,$ respectively, with the conditions $0\le \gamma,\delta,\eta \le 1$ and $0\le {\gamma }^{+}+{\delta }^{+}+{\eta }^{+}\le 3$, where $\gamma \in h\left(x\right),$ $\delta \in k(x),$ $\eta \in f(x),$ ${\gamma }^{+}\in {h}^{+}\left(x\right)=\bigcup_{\gamma \in t\left(x\right)}\mathrm{max}\left\{\gamma \right\},$ ${\delta }^{+}\in {k}^{+}\left(x\right)=\bigcup_{\delta \in k\left(x\right)}\mathrm{max}\left\{\delta \right\}$ and ${\eta }^{+}\in {f}^{+}\left(x\right)=\bigcup_{\eta \in f\left(x\right)}\mathrm{max}\left\{\eta \right\}$ for $x\in X.$

For convenience, the three tuple $n(x)=\{ \left(h\left(x\right),k\left(x\right),f(x)\right)\}$ is called a sigle-valued neutrosophic hesitant fuzzy number (SVNHFN), which is denoted by the simplified symbol $n=\{ h,k,f\}.$

Here, we obviously can see that a SVNHFS consists of three parts, i.e., the truth-membership hesitancy function, the indeterminacy-membership hesitancy function and the falsity-membership hesitancy function. Thus, the FSs, IFSs, HFSs and SVNSs can be regarded as special cases of SVNHFSs.

It is noted that the number of values in different SVNHFNs might be different. Şahin and Liu (2016) proposed to produce the same number of elements through adding some elements to the SVNHFNs which has less number of elements. The selection of this operation mainly depends on the decision makers’ risk preference. To operate correctly, they gave the following regulation: (1) all possible values in each membership of the SVNHFN are arranged in an increasing order, (2) pessimists expect unfavorable outcomes and may add the minimum value of truth-membership degrees and maximum values of indeterminacy-membership degrees and falsity-membership degrees, respectively, (3) optimists anticipate desirable outcomes and may add the maximum value of the truth-membership degrees and minimum values of indeterminacy-membership degrees and falsity-membership degrees, respectively. In this paper, we will adopt optimistic thinking.

To compare the SVNHFNs, (Ye 2014) gave the following comparative laws based on the cosine measure.

Definition 5

(Ye 2014) Let ${n}_{1}=\{ {h}_{1},{k}_{1},{f}_{1}\}$ be a SVNHFN, and $\widetilde{n}=\{\{1\},\{0\},\{0\}\}$ be an ideal SVNHFN, the cosine measure between ${n}_{1}$ and $\widetilde{n}$ can be defined as follows:

$$ \cos \left( {n_{1},\tilde{n}} \right) = \frac{{\frac{1}{{\# h_{1} }}\mathop \sum \nolimits_{i = 1}^{{\# h_{1} }} \gamma_{i} }}{{\sqrt {\left( {\frac{1}{{\# h_{1} }}\mathop \sum \nolimits_{i = 1}^{{\# h_{1} }} \gamma_{i} } \right)^{2} + \left( {\frac{1}{{\# k_{1} }}\mathop \sum \nolimits_{i = 1}^{{\# k_{1} }} \left( {1 - \delta_{i} } \right)} \right)^{2} + \left( {\frac{1}{{\# f_{1} }}\mathop \sum \nolimits_{i = 1}^{{\# f_{1} }} \left( {1 - \eta_{i} } \right)} \right)^{2} } }} $$

(5)

where $\#{h}_{1},\#{k}_{1}$ and $\#{f}_{1}$ denote the number of elements in ${h}_{1},{k}_{1}$ and ${f}_{1},$ respectively.

Definition 6

Peng et al. 2017c) Let ${n}_{1}$ and ${n}_{2}$ be two SVNHFNs, then the comparison approach can be defined as follows:

• (1) If $\mathrm{cos}\left({n}_{1},\widetilde{n}\right)>\mathrm{cos}\left({n}_{2},\widetilde{n}\right)$ then ${n}_{1}$ is greater than ${n}_{2}$ and denoted ${n}_{1}\succ {n}_{2}$

• (2) If $\mathrm{cos}\left({n}_{1},\widetilde{n}\right)=\mathrm{cos}\left({n}_{2},\widetilde{n}\right)$, then ${n}_{1}$ is equal to ${n}_{2}$ and denoted ${n}_{1}={n}_{2}.$

2.2 The existing distance measures of SVNHFNs

Assume that ${n}_{1}=\{ {h}_{1},{k}_{1},{f}_{1}\}$ and ${n}_{2}=\{ {h}_{2},{k}_{2},{f}_{2}\}$ is two SVNHFNs on $X.$ Şahin and Küçük (2015) defined some distance measures between them as follows:

Generalized single-valued neutrosophic hesitant fuzzy normalized distance, for $\lambda >0;$

$${d}_{1}\left({n}_{1},{n}_{2}\right)={\left(\frac{1}{3}\left(\frac{1}{\#h}\sum_{j=1}^{\#h}{\left|{h}_{1}^{\sigma \left(j\right)}-{h}_{2}^{\sigma \left(j\right)}\right|}^{\lambda }+\frac{1}{\#k}\sum_{j=1}^{\#k}{\left|{k}_{1}^{\sigma \left(j\right)}-{k}_{2}^{\sigma \left(j\right)}\right|}^{\lambda }+\frac{1}{\#f}\sum_{j=1}^{\#f}{\left|{f}_{1}^{\sigma \left(j\right)}-{f}_{2}^{\sigma \left(j\right)}\right|}^{\lambda }\right)\right)}^{\frac{1}{\lambda }},$$

(6)

where $\lambda >0$ and $\#h=\mathrm{max}\left(\#{h}_{1},\#{h}_{2}\right),$ $\#k=\mathrm{max}\left(\#{k}_{1},\#{k}_{2}\right)$ and $\#f=\mathrm{max}\left(\#{f}_{1},\#{f}_{2}\right).$

• i. If λ = 1, Eq. (3) reduces a single-valued neutrosophic hesitant fuzzy normalized Hamming distance:

  $${d}_{2}\left({n}_{1},{n}_{2}\right)=\frac{1}{3}\left(\frac{1}{\#h}\sum_{j=1}^{\#h}\left|{h}_{1}^{\sigma \left(j\right)}-{h}_{2}^{\sigma \left(j\right)}\right|+\frac{1}{\#k}\sum_{j=1}^{\#k}\left|{k}_{1}^{\sigma \left(j\right)}-{k}_{2}^{\sigma \left(j\right)}\right|+\frac{1}{\#f}\sum_{j=1}^{\#f}\left|{f}_{1}^{\sigma \left(j\right)}-{f}_{2}^{\sigma \left(j\right)}\right|\right).$$

  (7)

• ii. If λ = 2, Eq. (3) reduces a single-valued neutrosophic hesitant fuzzy normalized Euclidean distance:

  $${d}_{3}\left({n}_{1},{n}_{2}\right)={\left(\frac{1}{3}\left(\frac{1}{\#h}\sum_{j=1}^{\#h}{\left|{h}_{1}^{\sigma \left(j\right)}-{h}_{2}^{\sigma \left(j\right)}\right|}^{2}+\frac{1}{\#k}\sum_{j=1}^{\#k}{\left|{k}_{1}^{\sigma \left(j\right)}-{k}_{2}^{\sigma \left(j\right)}\right|}^{2}+\frac{1}{\#f}\sum_{j=1}^{\#f}{\left|{f}_{1}^{\sigma \left(j\right)}-{f}_{2}^{\sigma \left(j\right)}\right|}^{\lambda }\right)\right)}^\frac{1}{2}.$$

  (8)

3 Some novel concepts for SVNHFNs

In this section, we define the neutrosophic hesitancy index (NHI) for the SVNHFNs. Then, we develop some novel distance measures based on the NHI.

3.1 The neutrosophic hesitancy index (NHI) of SVNHFNs

Definition 7

Let $n=\{h,k,f\}$ be a SVNHFN, then the truth-membership hesitancy index $i\left( {n_{T} } \right),$ indeterminacy-membership hesitancy index $i\left( {n_{I} } \right)$ and falsity-membership hesitancy index $i\left( {n_{F} } \right)$ of $n$ are defined by, respectively,

$$ \begin{array}{*{20}l} {\left( {\mathbf{1}} \right)} \hfill & {i\left( {n_{T} } \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{if}} \# h = 1} \hfill \\ {2\left( {\frac{{\mathop \sum \nolimits_{i > j = 1}^{\# h} \left| {\gamma_{i} - \gamma_{j} } \right|}}{{\# h \times \left( {\# h - 1} \right)}}} \right),} \hfill & { {\text{if}} \# h > 1} \hfill \\ \end{array} } \right.;} \hfill \\ {\left( {\mathbf{2}} \right)} \hfill & {i\left( {n_{I} } \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{if}} \# k = 1} \hfill \\ {2\left( {\frac{{\mathop \sum \nolimits_{i > j = 1}^{\# k} \left| {\delta_{i} - \delta_{j} } \right|}}{{\# k \times \left( {\# k - 1} \right)}}} \right),} \hfill & { {\text{if}} \# k > 1} \hfill \\ \end{array} } \right.;} \hfill \\ {\left( {\mathbf{3}} \right)} \hfill & {i\left( {n_{F} } \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{if}} \# f = 1} \hfill \\ {2\left( {\frac{{\mathop \sum \nolimits_{i > j = 1}^{\# f} \left| {\eta_{i} - \eta_{j} } \right|}}{{\# f \times \left( {\# f - 1} \right)}}} \right),} \hfill & { {\text{if}} \# f > 1} \hfill \\ \end{array} } \right.} \hfill \\ \end{array}. $$

(9)

Then, the NHI of the SVNHFN $n$ is defined by

$$i\left(n\right)=\frac{1}{3}\left(\mathcal{i}\left({n}_{T}\right)+\mathcal{i}\left({n}_{I}\right)+\mathcal{i}\left({n}_{F}\right)\right).$$

(10)

Proposition 1

Let $n=\{h,k,f\}$ be a SVNHFN, and ${n}^{c}$ be the complement of $n,$ defined by ${n}^{c}=\{f,1-k,h\}.$ Then, the NHIs of the SVNHFNs $n$ and ${n}^{c},$ denoted by $i\left(n\right)$ and $i\left({n}^{c}\right),$ respectively, satisfy the following properties:

• (1) $0\le i\left(n\right)\le 1;$

• (2) $i\left(n\right)=i\left({n}^{c}\right).$

Proof:

• (1) It is obvious.

  $$ \begin{array}{*{20}l} {\left( {\mathbf{1}} \right)} \hfill & {i\left( {n_{T}^{c} } \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\quad \quad \quad \quad {\text{if}} \# f = 1} \hfill \\ {2\left( {\frac{{\mathop \sum \nolimits_{i > j = 1}^{\# f} \left| {\eta_{i} - \eta_{j} } \right|}}{{\# f \times \left( {\# f - 1} \right)}}} \right),} \hfill & {\quad \quad \quad \quad {\text{if}} \# f > 1} \hfill \\ \end{array} } \right.;} \hfill \\ {\left( {\mathbf{2}} \right)} \hfill & {i\left( {n_{I}^{c} } \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{if}} \# k = 1} \hfill \\ {2\left( {\frac{{\mathop \sum \nolimits_{i > j = 1}^{\# k} \left| {\left( {1 - \delta_{i} } \right) - \left( {1 - \delta_{j} } \right)} \right|}}{{\# k \times \left( {\# k - 1} \right)}}} \right),} \hfill & { {\text{if}} \# k > 1} \hfill \\ \end{array} } \right.;} \hfill \\ {\left( {\mathbf{3}} \right)} \hfill & {i\left( {n_{F}^{c} } \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\quad \quad \quad \quad {\text{if}} \# h = 1} \hfill \\ {2\left( {\frac{{\mathop \sum \nolimits_{i > j = 1}^{\# h} \left| {\gamma_{i} - \gamma_{j} } \right|}}{{\# h \times \left( {\# h - 1} \right)}}} \right),} \hfill & { \quad \quad \quad \quad {\text{if}} \# h > 1} \hfill \\ \end{array} } \right..} \hfill \\ \end{array} $$

Since for $i>j=1,$ $\left|\left({1-\delta }_{i}\right)-\left(1-{\delta }_{j}\right)\right|=\left|{\delta }_{i}-{\delta }_{j}\right|,$ we can obtain $i\left(n\right)=i\left({n}^{c}\right)$ obviously.

Thus, the NHI is a measure of the pair-wise deviations among each of possible membership values in the SVNHFN. Therefore, it can be used to determine the degree of hesitancy of an organization or individual. For example, in a group decision making with a reference set $X=\{x\},$ assume that there two decision makers ${d}_{1}$ and ${d}_{2}$, and their preference information is expressed as

$${n}_{1}=\langle x,\left\{0.3, 0.4, 0.6\right\}, \left\{0.1\right\}, \left\{0.3, 0.4\right\}\rangle ;$$

$${n}_{2}=\langle x,\{0.2, 0.7\}, \{0.1, 0.2\}, \{0.3, 0.6\}\rangle $$

In order to compare the hesitancy of decision makers in decision-making process, we can calculate their NHIs as follows;

$$i\left({n}_{1}\right)=\frac{2}{3}\times \left(\frac{\left|0.3-0.4\right|+\left|0.3-0.6\right|+\left|0.4-0.6\right|}{6}+0+\frac{\left|0.3-0.4\right|}{2}\right)=0.1$$

and

$$i\left({n}_{2}\right)=\frac{2}{3}\times \left(\frac{\left|0.2-0.7\right|}{2}+\frac{\left|0.1-0.2\right|}{2}+\frac{\left|0.3-0.6\right|}{2}\right)=0.3.$$

Then, the NHIs of decision makers ${d}_{1}$ and ${d}_{2}$ are obtained as $0.1$ and $0.3,$ respectively. Moreover, it is noted that the larger the range among the values in each membership of SVNHFN is, the greater the NHI of SVNHFN is.

3.2 A comparison method based on NHI for SVNHFNS

In the following, we develop a new approach to determine magnitude of two SVNHFNs, which considers simultaneously the cosine values and the NHI of SVNHFNs.

Proposition 1

Let ${n}_{1}=\{{h}_{1},{k}_{1},{f}_{1}\}$ and ${n}_{2}=\{{h}_{2},{k}_{2},{f}_{2}\}$ be two SVNHFNs, and $\widetilde{n}$ be the ideal SVNHFN. If

$${\gamma }_{1}^{\sigma \left(j\right)}\le {\gamma }_{2}^{\sigma \left(j\right)},{\delta }_{1}^{\sigma \left(j\right)}\ge {\delta }_{2}^{\sigma \left(j\right)},{\eta }_{1}^{\sigma \left(j\right)}\ge {\eta }_{2}^{\sigma \left(j\right)}\left(j=\mathrm{1,2},\dots,n\right)\Rightarrow \mathrm{cos}\left({n}_{1},\widetilde{n}\right)\le \mathrm{cos}\left({n}_{2},\widetilde{n}\right).$$

Definition 8

Let ${n}_{1}=\{{h}_{1},{k}_{1},{f}_{1}\}$ and ${n}_{2}=\{{h}_{2},{k}_{2},{f}_{2}\}$ be two SVNHFNs. Then, the partial order of SVNHFNs denoted by $"\preccurlyeq "$ is defined as:

$${n}_{1}\preccurlyeq {n}_{2}\iff {\gamma }_{1}^{\sigma \left(j\right)}\le {\gamma }_{2}^{\sigma \left(j\right)},{\delta }_{1}^{\sigma \left(j\right)}\ge {\delta }_{2}^{\sigma \left(j\right)},{\eta }_{1}^{\sigma \left(j\right)}\ge {\eta }_{2}^{\sigma \left(j\right)}\left(j=\mathrm{1,2},\dots,n\right), \mathrm{and}\; i\left({n}_{1}\right)\ge i\left({n}_{2}\right).$$

Definition 9

Let ${n}_{1}=\{{h}_{1},{k}_{1},{f}_{1}\}$ and ${n}_{2}=\{{h}_{2},{k}_{2},{f}_{2}\}$ be two SVNHFNs, and $\widetilde{n}$ be the ideal SVNHFN. Assume that $i\left({n}_{1}\right)$ and $i\left({n}_{2}\right)$ are the NHIs of ${n}_{1}$ and ${n}_{2},$ respectively. Then,

• (1) if $\mathrm{cos}\left({n}_{1},\widetilde{n}\right)>\mathrm{cos}\left({n}_{2},\widetilde{n}\right)$ then ${n}_{1}$ is greater than ${n}_{2}$ and denoted ${n}_{1}\succ {n}_{2}$,

• (2) if $\mathrm{cos}\left({n}_{1},\widetilde{n}\right)=\mathrm{cos}\left({n}_{2},\widetilde{n}\right),$ then

• i. if $i\left({n}_{1}\right)<i\left({n}_{2}\right)\Rightarrow {n}_{1}$ is greater than ${n}_{2}$ and denoted ${n}_{1}\succ {n}_{2}$

  • iii. if $i\left({n}_{1}\right)=i\left({n}_{2}\right)\Rightarrow {n}_{1}$ is equal to ${n}_{2}$ and denoted ${n}_{1}={n}_{2}.$

3.3 Novel distance measures for SVNHFNs

By taking the NHI of SVNHFNs into account, we propose the novel neutrosophic Hamming and Euclidean distance measures, respectively.

Definition 10

Let ${n}_{1}=\{{h}_{1},{k}_{1},{f}_{1}\}$ and ${n}_{2}=\{{h}_{2},{k}_{2},{f}_{2}\}$ be two SVNHFNs on $X$, $\lambda >0$ and $\#h=\mathrm{max}\left(\#{h}_{1},\#{h}_{2}\right),$ $\#k=\mathrm{max}\left(\#{k}_{1},\#{k}_{2}\right)$ and $\#f=\mathrm{max}\left(\#{f}_{1},\#{f}_{2}\right).$ Then, the novel single-valued neutrosophic hesitant fuzzy generalized distance of SVNHFNs can be defined by.

$$ \begin{aligned} d_{4} \left( {n_{1},n_{2} } \right) = & \left\{ {\frac{1}{4}\left( {\frac{1}{\# h}\mathop \sum \limits_{j = 1}^{\# h} \left| {h_{1}^{\sigma \left( j \right)} - h_{2}^{\sigma \left( j \right)} } \right|^{\lambda } + \frac{1}{\# k}\mathop \sum \limits_{j = 1}^{\# k} \left| {k_{1}^{\sigma \left( j \right)} - k_{2}^{\sigma \left( j \right)} } \right|^{\lambda } } \right.} \right. \\ & \left. {\left. { + \frac{1}{\# f}\mathop \sum \limits_{j = 1}^{\# f} \left| {f_{1}^{\sigma \left( j \right)} - f_{2}^{\sigma \left( j \right)} } \right|^{\lambda } + \left| {i\left( {n_{1} } \right) - i\left( {n_{2} } \right)} \right|^{\lambda } } \right)} \right\}^{{\frac{1}{\lambda }}} \\ \end{aligned} $$

(11)

where ${h}_{1}^{\sigma \left(j\right)},{h}_{2}^{\sigma \left(j\right)};$ ${k}_{1}^{\sigma \left(j\right)},{k}_{2}^{\sigma \left(j\right)}$ and ${f}_{1}^{\sigma \left(j\right)},{f}_{2}^{\sigma \left(j\right)}$ are the $j$ th smallest value of truth-membership degree, indeterminacy-membership degree and falsity-membership degree of ${n}_{1}$ and ${n}_{2},$ respectively, and.

$$ \begin{aligned} i\left( {n_{1} } \right) = & \frac{1}{3}\left( {i\left( {n_{{h_{1} }} } \right) + i\left( {n_{{k_{1} }} } \right) + i\left( {n_{{f_{1} }} } \right)} \right) \\ = & \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{if}} \# h = \# k = \# f = 1} \hfill \\ {\frac{2}{3}\left( {\frac{{\mathop \sum \nolimits_{i > j = 1}^{\# h} \left| {\gamma_{1}^{\sigma \left( i \right)} - \gamma_{1}^{\sigma \left( j \right)} } \right|}}{{\# h \times \left( {\# h - 1} \right)}} + \frac{{\mathop \sum \nolimits_{i > j = 1}^{\# k} \left| {\delta_{1}^{\sigma \left( j \right)} - \delta_{1}^{\sigma \left( j \right)} } \right|}}{{\# k \times \left( {\# k - 1} \right)}} + \frac{{\mathop \sum \nolimits_{i > j = 1}^{\# f} \left| {\eta_{1}^{\sigma \left( j \right)} - \eta_{1}^{\sigma \left( j \right)} } \right|}}{{\# f \times \left( {\# f - 1} \right)}}} \right),} \hfill & { {\text{if}}\; {\text{othervise}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

$$ \begin{aligned} i\left( {n_{2} } \right) = & \frac{1}{3}\left( {i\left( {n_{{h_{2} }} } \right) + i\left( {n_{{k_{2} }} } \right) + i\left( {n_{{f_{2} }} } \right)} \right) \\ = & \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{if}} \# h = \# k = \# f = 1} \hfill \\ {\frac{2}{3}\left( {\frac{{\mathop \sum \nolimits_{i > j = 1}^{\# h} \left| {\gamma_{2}^{\sigma \left( i \right)} - \gamma_{2}^{\sigma \left( j \right)} } \right|}}{{\# h \times \left( {\# h - 1} \right)}} + \frac{{\mathop \sum \nolimits_{i > j = 1}^{\# k} \left| {\delta_{2}^{\sigma \left( j \right)} - \delta_{2}^{\sigma \left( j \right)} } \right|}}{{\# k \times \left( {\# k - 1} \right)}} + \frac{{\mathop \sum \nolimits_{i > j = 1}^{\# f} \left| {\eta_{2}^{\sigma \left( j \right)} - \eta_{2}^{\sigma \left( j \right)} } \right|}}{{\# f \times \left( {\# f - 1} \right)}}} \right),} \hfill & { {\text{if}}\; {\text{othervise}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

Here, if $\lambda =1,$ then it is called the novel single-valued neutrosophic hesitant fuzzy normalized Hamming distance and defined by

$$ \begin{aligned} d_{5} \left( {n_{1},n_{2} } \right) = & \left\{ {\frac{1}{4}\left( {\frac{1}{\# h}\mathop \sum \limits_{j = 1}^{\# h} \left| {h_{1}^{\sigma \left( j \right)} - h_{2}^{\sigma \left( j \right)} } \right| + \frac{1}{\# k}\mathop \sum \limits_{j = 1}^{\# k} \left| {k_{1}^{\sigma \left( j \right)} - k_{2}^{\sigma \left( j \right)} } \right|} \right.} \right. \\ & \left. {\left. { + \frac{1}{\# f}\mathop \sum \limits_{j = 1}^{\# f} \left| {f_{1}^{\sigma \left( j \right)} - f_{2}^{\sigma \left( j \right)} } \right|^{\lambda } + \left| {i\left( {n_{1} } \right) - i\left( {n_{2} } \right)} \right|} \right)} \right\} \\ \end{aligned} $$

(12)

and if $\lambda =2,$ then it is called the novel single-valued neutrosophic hesitant fuzzy normalized Euclidian distance and defined by

$$ \begin{aligned} d_{6} \left( {n_{1},n_{2} } \right) = & \left\{ {\frac{1}{4}\left( {\frac{1}{\# h}\mathop \sum \limits_{j = 1}^{\# h} \left| {h_{1}^{\sigma \left( j \right)} - h_{2}^{\sigma \left( j \right)} } \right|^{2} + \frac{1}{\# k}\mathop \sum \limits_{j = 1}^{\# k} \left| {k_{1}^{\sigma \left( j \right)} - k_{2}^{\sigma \left( j \right)} } \right|^{2} } \right.} \right. \\ & \left. {\left. { + \frac{1}{\# f}\mathop \sum \limits_{j = 1}^{\# f} \left| {f_{1}^{\sigma \left( j \right)} - f_{2}^{\sigma \left( j \right)} } \right|^{2} + \left| {i\left( {n_{1} } \right) - i\left( {n_{2} } \right)} \right|^{2} } \right)} \right\}^{\frac{1}{2}}. \\ \end{aligned} $$

(13)

Theorem 1

Let ${n}_{1}=\{{h}_{1},{k}_{1},{f}_{1}\},$ ${n}_{2}=\{{h}_{2},{k}_{2},{f}_{2}\}$ and ${n}_{3}=\{{h}_{3},{k}_{3},{f}_{3}\}$ be three SVNHFNs on $X,$ $\lambda >0$ and $\#h=\mathrm{max}\left(\#{h}_{1},\#{h}_{2},\#{h}_{3}\right),$ $\#k=\mathrm{max}\left(\#{k}_{1},\#{k}_{2},\#{k}_{3}\right)$ and $\#f=\mathrm{max}\left(\#{f}_{1},\#{f}_{2},\#{f}_{3}\right).$ Then, ${d}_{4}\left({n}_{1},{n}_{2}\right)$ satisfies the following conditions:

• (1) $0\le {d}_{4}\left({n}_{1},{n}_{2}\right)\le 1;$

• (2) ${d}_{4}\left({n}_{1},{n}_{2}\right)=0\Leftrightarrow {n}_{1}={n}_{2};$

• (3) ${d}_{4}\left({n}_{1},{n}_{2}\right)={d}_{4}\left({n}_{2},{n}_{1}\right)$;

• (4) ${d}_{4}\left({n}_{1},{n}_{2}\right)\le {d}_{4}\left({n}_{1},{n}_{3}\right)$ and ${d}_{4}\left({n}_{2},{n}_{3}\right)\le {d}_{4}\left({n}_{1},{n}_{3}\right),$ if ${n}_{1}\le {n}_{2}\le {n}_{3}.$

Proof:

• (1) It is obvious.

• (2) If ${d}_{4}\left({n}_{1},{n}_{2}\right)=0,$ we have

  $$\frac{1}{\#h}\sum_{j=1}^{\#h}{\left|{h}_{1}^{\sigma \left(j\right)}-{h}_{2}^{\sigma \left(j\right)}\right|}^{\lambda }=\frac{1}{\#k}\sum_{j=1}^{\#k}{\left|{k}_{1}^{\sigma \left(j\right)}-{k}_{2}^{\sigma \left(j\right)}\right|}^{\lambda }=\frac{1}{\#f}\sum_{j=1}^{\#f}{\left|{f}_{1}^{\sigma \left(j\right)}-{f}_{2}^{\sigma \left(j\right)}\right|}^{\lambda }=0$$

and

$${\left|\mathcal{i}\left({n}_{1}\right)-\mathcal{i}\left({n}_{2}\right)\right|}^{\lambda }=0.$$

Then it follows that ${h}_{1}^{\sigma \left(j\right)}-{h}_{2}^{\sigma \left(j\right)}=0,$ ${k}_{1}^{\sigma \left(j\right)}-{k}_{2}^{\sigma \left(j\right)}=0,$,${f}_{1}^{\sigma \left(j\right)}-{f}_{2}^{\sigma \left(j\right)}=0,$ and $\mathcal{i}\left({n}_{1}\right)-\mathcal{i}\left({n}_{2}\right)=0.$ Thus we get ${h}_{1}^{\sigma \left(j\right)}={h}_{2}^{\sigma \left(j\right)},$ ${k}_{1}^{\sigma \left(j\right)}={k}_{2}^{\sigma \left(j\right)},$ ${f}_{1}^{\sigma \left(j\right)}={f}_{2}^{\sigma \left(j\right)}$ and $\mathcal{i}\left({n}_{1}\right)=\mathcal{i}\left({n}_{2}\right),$ and so ${n}_{1}={n}_{2}.$ Moreover, if ${n}_{1}={n}_{2},$ we can easily obtain that ${d}_{4}\left({n}_{1},{n}_{2}\right)=0.$

• (3)
  $$ \begin{aligned} d_{4} \left( {n_{1},n_{2} } \right) =& \left\{ {\frac{1}{4}\left( {\frac{1}{{\# h}}\mathop \sum \limits_{{j = 1}}^{{\# h}} \left| {h_{1}^{{\sigma \left( j \right)}}- h_{2}^{{\sigma \left( j \right)}} } \right|^{\lambda }+ \frac{1}{{\# k}}\mathop \sum \limits_{{j = 1}}^{{\# k}} \left| {k_{1}^{{\sigma \left( j \right)}}- k_{2}^{{\sigma \left( j \right)}} } \right|^{\lambda } } \right.} \right. \\ & \left. {\left. { + \frac{1}{{\# f}}\mathop \sum \limits_{{j = 1}}^{{\# f}} \left| {f_{1}^{{\sigma \left( j \right)}}- f_{2}^{{\sigma \left( j \right)}} } \right|^{\lambda }+ \left| {i\left( {n_{1} } \right) - i\left( {n_{2} } \right)} \right|^{\lambda } } \right)} \right\}^{{\frac{1}{\lambda }}}\\ =& \left\{ {\frac{1}{4}\left( {\frac{1}{{\# h}}\mathop \sum \limits_{{j = 1}}^{{\# h}} \left| {h_{2}^{{\sigma \left( j \right)}}- h_{1}^{{\sigma \left( j \right)}} } \right|^{\lambda }+ \frac{1}{{\# k}}\mathop \sum \limits_{{j = 1}}^{{\# k}} \left| {k_{2}^{{\sigma \left( j \right)}}- k_{1}^{{\sigma \left( j \right)}} } \right|^{\lambda } } \right.} \right. \\ & \left. {\left. { + \frac{1}{{\# f}}\mathop \sum \limits_{{j = 1}}^{{\# f}} \left| {f_{1}^{{\sigma \left( j \right)}}- f_{2}^{{\sigma \left( j \right)}} } \right|^{\lambda }+ \left| {i\left( {n_{1} } \right) - i\left( {n_{2} } \right)} \right|^{\lambda } } \right)} \right\}^{{\frac{1}{\lambda }}}= d_{4} \left( {n_{2},n_{1} } \right). \\\end{aligned}$$

• (4) Based on Definition 4, since ${n}_{1}\le {n}_{2}\le {n}_{3}$, we have ${h}_{1}^{\sigma \left(j\right)}\le {h}_{2}^{\sigma \left(j\right)}\le {h}_{3}^{\sigma \left(j\right)}$, ${k}_{1}^{\sigma \left(j\right)}\ge {k}_{2}^{\sigma \left(j\right)}\ge {k}_{3}^{\sigma \left(j\right)}$ and ${f}_{1}^{\sigma \left(j\right)}\ge {f}_{2}^{\sigma \left(j\right)}\ge {f}_{3}^{\sigma \left(j\right)}(j=\mathrm{1,2},\dots,\#h=\#k=\#f)$, and $\mathcal{i}\left({n}_{1}\right)\ge \mathcal{i}\left({n}_{2}\right)\ge \mathcal{i}\left({n}_{3}\right)$. Thus, it follows that

  $$ \begin{gathered} \left| {h_{1}^{\sigma \left( j \right)} - h_{2}^{\sigma \left( j \right)} } \right|^{\lambda } \le \left| {h_{1}^{\sigma \left( j \right)} - h_{3}^{\sigma \left( j \right)} } \right|^{\lambda },\left| {k_{1}^{\sigma \left( j \right)} - k_{2}^{\sigma \left( j \right)} } \right|^{\lambda } \le \left| {k_{1}^{\sigma \left( j \right)} - k_{3}^{\sigma \left( j \right)} } \right|^{\lambda },\left| {f_{1}^{\sigma \left( j \right)} - f_{2}^{\sigma \left( j \right)} } \right|^{\lambda } \le \left| {f_{1}^{\sigma \left( j \right)} - f_{3}^{\sigma \left( j \right)} } \right|^{\lambda } \hfill \\ \left| {h_{2}^{\sigma \left( j \right)} - h_{3}^{\sigma \left( j \right)} } \right|^{\lambda } \le \left| {h_{1}^{\sigma \left( j \right)} - h_{3}^{\sigma \left( j \right)} } \right|^{\lambda },\left| {k_{2}^{\sigma \left( j \right)} - k_{3}^{\sigma \left( j \right)} } \right|^{\lambda } \le \left| {k_{1}^{\sigma \left( j \right)} - k_{3}^{\sigma \left( j \right)} } \right|^{\lambda },\left| {f_{2}^{\sigma \left( j \right)} - f_{3}^{\sigma \left( j \right)} } \right|^{\lambda } \le \left| {f_{1}^{\sigma \left( j \right)} - f_{3}^{\sigma \left( j \right)} } \right|^{\lambda } \hfill \\ \end{gathered} $$

and

$$ \begin{gathered} \left| {i\left( {n_{1} } \right) - i\left( {n_{2} } \right)} \right|^{\lambda } \le \left| {i\left( {n_{1} } \right) - i\left( {n_{3} } \right)} \right|^{\lambda }, \hfill \\ \left| {i\left( {n_{2} } \right) - i\left( {n_{3} } \right)} \right|^{\lambda } \le \left| {i\left( {n_{1} } \right) - i\left( {n_{3} } \right)} \right|^{\lambda }. \hfill \\ \end{gathered} $$

So

$$ \begin{gathered} \left\{ {\frac{1}{4}\left( {\frac{1}{\# h}\mathop \sum \limits_{j = 1}^{\# h} \left| {h_{1}^{\sigma \left( j \right)} - h_{2}^{\sigma \left( j \right)} } \right|^{\lambda } + \frac{1}{\# k}\mathop \sum \limits_{j = 1}^{\# k} \left| {k_{1}^{\sigma \left( j \right)} - k_{2}^{\sigma \left( j \right)} } \right|^{\lambda } + \frac{1}{\# f}\mathop \sum \limits_{j = 1}^{\# f} \left| {f_{1}^{\sigma \left( j \right)} - f_{2}^{\sigma \left( j \right)} } \right|^{\lambda } + \left| {i\left( {n_{1} } \right) - i\left( {n_{2} } \right)} \right|^{\lambda } } \right)} \right\}^{{\frac{1}{\lambda }}} \hfill \\ \le \left\{ {\frac{1}{4}\left( {\frac{1}{\# h}\mathop \sum \limits_{j = 1}^{\# h} \left| {h_{1}^{\sigma \left( j \right)} - h_{3}^{\sigma \left( j \right)} } \right|^{\lambda } + \frac{1}{\# k}\mathop \sum \limits_{j = 1}^{\# k} \left| {k_{1}^{\sigma \left( j \right)} - k_{3}^{\sigma \left( j \right)} } \right|^{\lambda } + \frac{1}{\# f}\mathop \sum \limits_{j = 1}^{\# f} \left| {f_{1}^{\sigma \left( j \right)} - f_{3}^{\sigma \left( j \right)} } \right|^{\lambda } + \left| {i\left( {n_{1} } \right) - i\left( {n_{3} } \right)} \right|^{\lambda } } \right)} \right\}^{{\frac{1}{\lambda }}}, \hfill \\ \left\{ {\frac{1}{4}\left( {\frac{1}{\# h}\mathop \sum \limits_{j = 1}^{\# h} \left| {h_{2}^{\sigma \left( j \right)} - h_{3}^{\sigma \left( j \right)} } \right|^{\lambda } + \frac{1}{\# k}\mathop \sum \limits_{j = 1}^{\# k} \left| {k_{2}^{\sigma \left( j \right)} - k_{3}^{\sigma \left( j \right)} } \right|^{\lambda } + \frac{1}{\# f}\mathop \sum \limits_{j = 1}^{\# f} \left| {f_{2}^{\sigma \left( j \right)} - f_{3}^{\sigma \left( j \right)} } \right|^{\lambda } + \left| {i\left( {n_{2} } \right) - i\left( {n_{3} } \right)} \right|^{\lambda } } \right)} \right\}^{{\frac{1}{\lambda }}} \hfill \\ \le \left\{ {\frac{1}{4}\left( {\frac{1}{\# h}\mathop \sum \limits_{j = 1}^{\# h} \left| {h_{1}^{\sigma \left( j \right)} - h_{3}^{\sigma \left( j \right)} } \right|^{\lambda } + \frac{1}{\# k}\mathop \sum \limits_{j = 1}^{\# k} \left| {k_{1}^{\sigma \left( j \right)} - k_{3}^{\sigma \left( j \right)} } \right|^{\lambda } + \frac{1}{\# f}\mathop \sum \limits_{j = 1}^{\# f} \left| {f_{1}^{\sigma \left( j \right)} - f_{3}^{\sigma \left( j \right)} } \right|^{\lambda } + \left| {i\left( {n_{1} } \right) - i\left( {n_{3} } \right)} \right|^{\lambda } } \right)} \right\}^{{\frac{1}{\lambda }}}. \hfill \\ \end{gathered} $$

That is, we obtain the result ${d}_{4}\left({n}_{1},{n}_{2}\right)\le {d}_{4}\left({n}_{1},{n}_{3}\right)$ and${d}_{4}\left({n}_{2},{n}_{3}\right)\le {d}_{4}\left({n}_{1},{n}_{3}\right)$, if${n}_{1}\le {n}_{2}\le {n}_{3}$.

This completes the proof.

There are many of advantages of novel distance measures based on NHI. We present the following numerical example to compare the novel distance measures with the existing distance measures given in Sect. 2.3.

Example 1

Let ${n}_{1}=\left\{\left\{\mathrm{0.2,0.5}\right\},\left\{\mathrm{0.2,0.8}\right\},\left\{\mathrm{0.3,0.8}\right\}\right\}$, ${n}_{2}=\left\{\left\{\mathrm{0.1,0.6}\right\},\left\{\mathrm{0.3,0.7}\right\},\left\{\mathrm{0.5,0.6}\right\}\right\}$ and ${n}_{3}=\left\{\left\{\mathrm{0.3,0.4}\right\},\left\{\mathrm{0.4,0.6}\right\},\left\{\mathrm{0.4,0.7}\right\}\right\}$ be three SVNHFNs.

Considering all of the distance measures presented, we can obtain the corresponding distances between them. The obtained results are given in Table 1.

Table 1 Comparison of different distance measures

According to Table 1, it can clearly note that it is not possible to reach a comparison result by using the existing distance measures presented in Eqs. (7, 8). Since ${d}_{2}\left({n}_{1},{n}_{2}\right)={d}_{2}\left({n}_{1},{n}_{3}\right)$ and ${d}_{3}\left({n}_{1},{n}_{2}\right)={d}_{3}\left({n}_{1},{n}_{3}\right)$, it is logically expected to be ${n}_{2}={n}_{3}$. However, since ${n}_{2}\ne {n}_{3}$, these distance measures have counter-intuitive situations. If we use modified distance measures presented in Eqs. (12, 13), we can clearly know that the SVNHFN ${n}_{1}$ is farther from ${n}_{3}$ than ${n}_{2}$, which are in accordance with people’s intuition. Therefore, the modified distance measures are the most functional distance measures.

Now, we develop a novel approach to compare the magnitudes of two SVNHFNs, based on the novel distance measure of SVNHFNs.

3.4 A comparison method based on distance measure for SVNHFNS

There are a number of comparison techniques presenting the relationship between objects. In this subsection, we present a novel comparison method for SVNHFNs, based on the distance measure between each individual decision and ideal decision. The final decision is expected to be close to the positive ideal decision (PID) and far from the negative ideal decision (NID). Then, a comparison approach can be developed according to the PID. Therefore, it is easy to notice that the above proposed novel distance measure and ideal SVNHFN $\widetilde{n}=\{\{1\},\{0\},\{0\}\}$ can be used to determine the ranking order between two SVNHFNs.

Definition 11

Suppose that $n$ is a SVNHFNs on $X$ and $\widetilde{n}$ is the ideal SVNHFN, then $d(n,\widetilde{n})$ can be defined as follows:

$$ d_{7} \left( {n,\tilde{n}} \right) = \left\{ {\begin{array}{*{20}l} {\left\{ {\frac{1}{2}\left( {\begin{array}{*{20}l} {\frac{1}{3}\left( {\frac{1}{\# h}\mathop \sum \limits_{j = 1}^{\# h} \left| {1 - h^{\sigma \left( j \right)} } \right|^{\lambda } + \frac{1}{\# k}\mathop \sum \limits_{j = 1}^{\# k} \left| {k^{\sigma \left( j \right)} } \right|^{\lambda } + \frac{1}{\# f}\mathop \sum \limits_{j = 1}^{\# f} \left| {f^{\sigma \left( j \right)} } \right|^{\lambda } } \right)} \hfill \\ { + \frac{2}{3}\left( {\frac{{\mathop \sum \nolimits_{i > j = 1}^{\# h} \left| {\gamma^{\sigma \left( i \right)} - \gamma^{\sigma \left( j \right)} } \right|^{\lambda } }}{{\# h \times \left( {\# h - 1} \right)}} + \frac{{\mathop \sum \nolimits_{i > j = 1}^{\# k} \left| {\delta^{\sigma \left( j \right)} - \delta^{\sigma \left( j \right)} } \right|^{\lambda } }}{{\# k \times \left( {\# k - 1} \right)}} + \frac{{\mathop \sum \nolimits_{i > j = 1}^{\# f} \left| {\eta^{\sigma \left( j \right)} - \eta^{\sigma \left( j \right)} } \right|^{\lambda } }}{{\# f \times \left( {\# f - 1} \right)}}} \right)} \hfill \\ \end{array} } \right)} \right\}^{{\frac{1}{\lambda }}},} \hfill & {{\text{otherwise}}} \hfill \\ {\left\{ {\frac{1}{3}\left( {\left| {1 - h} \right|^{\lambda } + \left| k \right|^{\lambda } + \left| f \right|^{\lambda } } \right)} \right\}^{{\frac{1}{\lambda }}},} \hfill & {\# h = \# k = \# f = 1} \hfill \\ \end{array} } \right. $$

(14)

Here, it can be easily noted that if $n$ is located at $\widetilde{n}$ if and only if ${d}_{7}\left(n,\widetilde{n}\right)=0$, and for any two SVNHFNs ${n}_{1}$ and ${n}_{2}$, we have three different cases such as ${d}_{7}\left({n}_{1},\widetilde{n}\right)<{d}_{7}\left({n}_{2},\widetilde{n}\right)$, ${d}_{7}\left({n}_{1},\widetilde{n}\right)={d}_{7}\left({n}_{2},\widetilde{n}\right)$ or ${d}_{7}\left({n}_{1},\widetilde{n}\right)>{d}_{7}\left({n}_{2},\widetilde{n}\right)$. Then, we give the following comparative approach using the above cases.

Definition 12

Let ${n}_{1}$ and ${n}_{2}$ be two SVNHFNs on $X$ and $\widetilde{n}$ be the ideal SVNHFN; let ${d}_{7}\left({n}_{1},\widetilde{n}\right)$ and ${d}_{7}\left({n}_{2},\widetilde{n}\right)$ be the distance measures. Then,

• (1) if ${d}_{7}\left({n}_{1},\widetilde{n}\right)>{d}_{7}\left({n}_{2},\widetilde{n}\right)$, then ${n}_{1}$ is worse than or less preferred to ${n}_{2}$, and denoted by ${n}_{1}\prec {n}_{2}$;

• (2) if ${d}_{7}\left({n}_{1},\widetilde{n}\right)<{d}_{7}\left({n}_{2},\widetilde{n}\right)$, then ${n}_{1}$ is better than or preferred to ${n}_{2}$, and denoted by ${n}_{1}\succ {n}_{2}$;

• (3) if ${d}_{7}\left({n}_{1},\widetilde{n}\right)={d}_{7}\left({n}_{2},\widetilde{n}\right)$, then ${n}_{1}$ is indifferent to ${n}_{2}$, and denoted by ${n}_{1}\sim {n}_{2}$.

Example 2

Let ${n}_{1}$, ${n}_{2}$ and ${n}_{3}$ be three SVNHFNs given in Example 1, and $\widetilde{n}$ be an ideal SVNHFN, $\widetilde{n}=\{\{1\},\{0\},\{0\}\}$. Then, we prove an analysis according to all comparison techniques given in Definitions (6,9,11) and present it in Table 2.

Table 2 The different comparison results

According to Table 2, the ranking order obtained by Definition 6 is ${n}_{1}={n}_{2}={n}_{3}$ and it is not in accordance with people’s intuition. Using the comparison approaches presented in Definition 9 and Definition 11, we obtain this ranking as ${n}_{3}\succ {n}_{2}\succ {n}_{1}$. Obviously, this difference is due to the case where the comparison methods proposed in the both Definition 6 and Definition 9 are based on the NHIs of SVNHFNs in the practical decision-making process. Therefore, the developed comparison methods are more reasonable rather that the existing comparison method given in Definition 6 in the comparative process.

4 A distance-based extended QUALIFLEX method for MAGDM with SVNHFNs

In this section, by taking the developed distance-based comparison method account into, we present a new N-QUALIFLEX approach for solving of MCGDM problems under neutrosophic environment.

The decision steps of the N-QUALIFLEX are developed as follows:

4.1 The representation of MCGDM problems with SVNHFNs

Assume that $A=\left\{{A}_{1},{A}_{2},\dots,{A}_{m}\right\}$ denotes the collection of all alternatives, $C=\left\{{C}_{1},{C}_{2},\dots,{C}_{n}\right\}$ denotes the collection of all criteria, and $D=\left\{{D}_{1},{D}_{2},\dots,{D}_{t}\right\}$ denotes the collection of all decision makers. We use the SVNN ${n}_{ij}^{r}= \{{h}_{ij}^{r},{k}_{ij}^{r},{f}_{ij}^{r}\}$ to represent the evaluation value of the alternative ${A}_{i}$ with respect to the criterion ${C}_{j}$ given by the decision maker ${D}_{r}$. The decision matrix is expressed by ${N}^{r}={\left({n}_{ij}^{r}\right)}_{m\times n}$. The weights of criteria must be included in the decision-making process as they directly affect the decision process, and they are usually chosen from real numbers. However, for more realistic applications, the importance weights of criteria can be selected as the SVNNs in place of real numbers during the DM’s evaluation process. Assume that $W={\left({w}_{1},{w}_{2},\dots,{w}_{n}\right)}^{T}$ is the weight vector of criteria ${C}_{j} (j=\mathrm{1,2},\dots,n)$. Then, if each ${w}_{j}(j=\mathrm{1,2},\dots,n)$ is a SVNN, it can be denoted by ${w}_{j}=\left\{{h}_{{w}_{j}},{k}_{{w}_{j}},{f}_{{w}_{j}}\right\}(i=\mathrm{1,2},\dots,m;j=\mathrm{1,2},\dots,n)$, and ${h}_{{w}_{j}},{k}_{{w}_{j}},{f}_{{w}_{j}}\in \left[\mathrm{0,1}\right]$, whose ${h}_{{w}_{j}}$ is the degree of truth-membership of ${w}_{j}$, ${k}_{{w}_{j}}$ is the degree of indeterminacy-membership of ${w}_{j}$, and ${f}_{{w}_{j}}$ is the degree of falsity-membership of ${w}_{j}$.

From common senses, it is necessary to convert the different types of the attributes to same type. So, we can convert the attribute values of cost type into benefit type, and the transformed decision matrices are expressed by ${S}^{r}={\left({s}_{ij}^{r}\right)}_{m\times n}(i=\mathrm{1,2},\dots,m;j=\mathrm{1,2},\dots,n;r=\mathrm{1,2},\dots,t),$ where

$${s}_{ij}^{r}=\left\{\begin{array}{cc}{n}_{ij}^{r}=\left\{{h}_{ij}^{r},{k}_{ij}^{r},{f}_{ij}^{r}\right\},& \mathrm{ for \; maximizing \; criteria }\;{C}_{j}\\ {\left({n}_{ij}^{r}\right)}^{c}=\left\{{f}_{ij}^{r},1-{k}_{ij}^{r},{h}_{ij}^{r}\right\},& \mathrm{for \; minimizing \; criteria }\;{C}_{j}\end{array} (i=\mathrm{1,2},\dots,m;j=\mathrm{1,2},\dots,n)\right.$$

(15)

Here, ${\left({n}_{ij}\right)}^{c}$ is the complement of ${n}_{ij}$.

4.2 The developed N-QUALIFLEX approach

The aim of the subsection is to solve the MCGDM problems in which both the evaluations of alternatives with respect to criteria and the weights of criteria take the form of SVNNs. To do this, the classical QUALIFLEX approach is applied to single-valued neutrosophic hesitant fuzzy environment and an N-QUALIFLEX approach is developed based on the distance-based comparison method. The proposed method starts with the calculation of the concordance/discordance index based on consecutive permutations of all possible alternative orders.

Considering the set of alternatives $A=\left\{{A}_{1},{A}_{2},\dots,{A}_{n}\right\}$, assume that there exist $n!$ permutations of the ranking of the alternatives, and let ${K}_{p}$ denote the $p$ th permutation as: ${K}_{p}=\left(\dots,{A}_{\alpha },\dots,{A}_{\beta },\dots \right)$ $p=\mathrm{1,2},\dots,n!$, where ${A}_{\alpha }$, ${A}_{\beta }\in A$ and the alternative ${A}_{\alpha }$ is ranked higher than or equal to ${A}_{\beta }$.

The concordance/discordance index ${\Phi }_{j}^{p}({A}_{\alpha },{A}_{\beta })$ for each pair of alternatives $\left({A}_{\alpha },{A}_{\beta }\right),$ at the level of preorder according to the $j$ th criterion and the ranking corresponding to the $p$ th permutation, can be defined as follows:

$${\Phi }_{j}^{p}\left({A}_{\alpha },{A}_{\beta }\right)={d}_{7}\left({n}_{\alpha j},\widetilde{n}\right)-{d}_{7}\left({n}_{\beta j},\widetilde{n}\right).$$

(16)

According to the comparison method of SVNHFNs given in Definition 12, we can obtain the following results:

• (1) if ${\Phi }_{j}^{p}\left({A}_{\alpha },{A}_{\beta }\right)>0$, that is, ${d}_{7}\left({n}_{\alpha j},\widetilde{n}\right)>{d}_{7}\left({n}_{\beta j},\widetilde{n}\right)$ then ${A}_{\alpha }$ is in a position in front of ${A}_{\beta }$ under the $j$ th criterion; thus, it can be said easily that there is a concordance between the developed distance-based ranking orders and the preorders of ${A}_{\alpha }$ and ${A}_{\beta }$ under the $p$ th permutation,

• (2) if ${\Phi }_{j}^{p}\left({A}_{\alpha },{A}_{\beta }\right)=0$, that is, ${d}_{s}\left({n}_{\alpha j},\widetilde{n}\right)={d}_{s}\left({n}_{\beta j},\widetilde{n}\right)$ then ${A}_{\alpha }$ is in the same position as ${A}_{\beta }$; thus, there is the same relationship between the developed distance-based ranking orders and the preorders of ${A}_{\alpha }$ and ${A}_{\beta }$ under the $p$ th permutation,

• (3) if ${\Phi }_{j}^{p}\left({A}_{\alpha },{A}_{\beta }\right)<0$, that is, ${d}_{s}\left({n}_{\alpha j},\widetilde{n}\right)<{d}_{s}\left({n}_{\beta j},\widetilde{n}\right)$ then ${A}_{\alpha }$ is in a position in back of ${A}_{\beta }$; thus, it can be said easily that there is a discordance between the developed distance-based ranking orders and the preorders of ${A}_{\alpha }$ and ${A}_{\beta }$ under the $p$ th permutation.

Considering that the collective weights of criteria are characterized by SVNHFNs, we also utilize the developed distance measure of SVNHFNs and obtain the weighted aggregated concordance/discordance index ${\Phi }_{j}^{p}\left({A}_{\alpha },{A}_{\beta }\right)$ for each pair of alternatives $\left({A}_{\alpha },{A}_{\beta }\right)$ as follows:

$${\Phi }^{p}\left({A}_{\alpha },{A}_{\beta }\right)=\sum_{j=1}^{n}{\Phi }_{j}^{p}\left({A}_{\alpha },{A}_{\beta }\right)\times \left(1-{d}_{s}\left({W}_{j},\widetilde{n}\right)\right).$$

(17)

Then, we determine the comprehensive concordance/discordance index ${\Phi }^{p}$ for the $p$ th permutation as follows:

$${\Phi }^{p}=\sum_{{A}_{\alpha },{A}_{\beta }\in A}{\Phi }^{p}\left({A}_{\alpha },{A}_{\beta }\right)=\sum_{{A}_{\alpha },{A}_{\beta }\in A}\sum_{j=1}^{n}{\Phi }_{j}^{p}\left({A}_{\alpha },{A}_{\beta }\right)\times \left(1-{d}_{s}\left({W}_{j},\widetilde{n}\right)\right).$$

(18)

The comprehensive concordance index ${\Phi }^{p}$ can serve as the evaluation criterion of the chosen hypothesis for ranking the alternatives. The bigger the comprehensive concordance index of the permutation value is, the better the final ranking result of the alternatives is. Therefore, the optimal ranking order of alternatives can be obtained with respect to the values ${\Phi }^{p}$ of each permutation ${K}_{p}$, which is the permutation with the maximal value${\Phi }^{p}$, that is:

$${P}^{*}={\underset{p=1}{\mathrm{max}}}^{m!}\left\{{\Phi }^{p}\right\}.$$

(19)

4.3 An algorithm for the N-QUALIFLEX

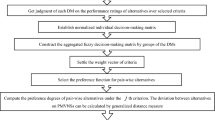
The developed N-QUALIFLEX approach can be listed in the following steps.

Step 1. Normalize the decision-making matrices by using Eq. (15).

Step 2. Determine all of the possible m! Permutation of the m alternatives.

Step 3. Obtain the concordance/discordance index ${\Phi }_{j}^{p}\left({A}_{\alpha },{A}_{\beta }\right)$ by using Eq. (16).

Step 4. Compute the weighted concordance/discordance indices ${\Phi }^{p}\left({A}_{\alpha },{A}_{\beta }\right)$ by using Eq. (17).

Step 5. Calculate the comprehensive concordance/discordance index ${\Phi }^{p}$ for the permutation ${K}_{p}$ by using Eq. (18).

Step 6. Determine the optimal ranking order of all alternatives according to the maximal comprehensive concordance/discordance index by using Eq. (19).

5 Application to selection of alternatives

We give an example of an MCGDM problem to present the application and effectiveness of the proposed decision-making approach.

In order to reduce its environmental impact and increase protection efficiency, a healthcare institution aims to buy the most suitable mask from its suppliers. Therefore, how to select the most effective supplier from several potential suppliers is a question of MCGDM. In this case, we choose three possible suppliers as alternative solutions, ${A}_{i}(i=\mathrm{1,2},3$). Each of alternatives is evaluated based on nine criteria, which are denoted by ${C}_{j}(j=\mathrm{1,2},3,\dots,9)$: filtration efficiency $({C}_{1})$, reusability $\left({C}_{2}\right),$ breathability $({C}_{3})$, destructibility $({C}_{4})$, production cost $({C}_{5})$, quality of raw materials $({C}_{6})$, face compatibility $\left({C}_{7}\right),$ lightness $({C}_{8})$ and uninterrupted supply $({C}_{9})$. Moreover, assume that all of the criteria are maximizing type. Then, three decision makers (DM1, DM2, DM3) provide their performance ratings for each alternatives with respect to each criterion. All possible evaluations for an alternative under each criterion are considered as a SVNN. Tables 3, 4, 5 and 6 present the initial evaluations of alternatives on each criterion and the weight information of criteria provided by the three DMs, respectively.

Table 3 The evaluations provided by DMs for the alternative ${A}_{1}$

Table 4 The evaluations provided by DMs for the alternative ${A}_{2}$

Table 5 The evaluations provided by DMs for the alternative ${A}_{3}$

Table 6 The weights of the criteria provided by three DMs

In the process of determining the collective values, the aggregated values that are the form of SVNHFNs are directly obtained from the performance ratings of DMs. The advantage of this process minimizes loss of information against aggregation operators and allows more realistic results for the decision process.

5.1 An illustration of the proposed method

To select the most suitable one from the possible alternatives, we use the proposed N-QUALIFLEX method described in Sect. 4. The procedure and computation results are summarized below.

Step 1 Since all of the criteria are the maximizing type, the normalized decision matrices are the same as the initial matrices.

Step 2 For $m=3$, we have 6(3! = 6) permutations of the rankings for all alternatives which are presented as follows:

$$ \begin{aligned} K_{1}=& \left\{ {A_{1},A_{2},A_{3} } \right\},K_{2}= \left\{ {A_{1},A_{3},A_{2} } \right\}, \\K_{3}=& \left\{ {A_{2},A_{1},A_{3} } \right\}K_{4}= \left\{ {A_{2},A_{3},A_{1} } \right\}, \\K_{5}=& \left\{ {A_{3},A_{1},A_{2} } \right\},K_{6}= \left\{ {A_{3},A_{2},A_{1} } \right\} \\\end{aligned}$$

Step 3 According to the Hamming distance measure given by Eq. (12), for each pair of alternatives ${A}_{\alpha },{A}_{\beta }$ in the permutation ${K}_{p}$ with respect to each criterion ${C}_{j}$, the concordance/discordance index ${\Phi }_{j}^{p}\left({A}_{\alpha },{A}_{\beta }\right)$ can be calculated by employing Eq. (16), and the results are presented in (Tables 7, 8 and 9).

Table 7 The results of the concordance/discordance index for ${K}_{1}$ and ${K}_{2}$

Table 8 The results of the concordance/discordance index for ${K}_{3}$ and ${K}_{4}$

Table 9 The results of the concordance/discordance index for ${K}_{5}$ and ${K}_{6}$

Step 4 We compute the weighted concordance/discordance indices ${\Phi }^{p}\left({A}_{\alpha },{A}_{\beta }\right)$ by using Eq. (17) and present them in Table 10.

Table 10 The results of the weighted concordance/discordance index

Step 5 In the step, we compute the comprehensive concordance/discordance index ${\Phi }^{p}(p=\mathrm{1,2},\mathrm{3,4},\mathrm{5,6})$ by using Eq. (18) as follows:

$${\Phi }^{1}=0.074, {\Phi }^{2}=0.055, {\Phi }^{3}=0.019, {\Phi }^{4}=-0.055,{\Phi }^{5}=-0.019, {\Phi }^{6}=-0.074.$$

Step 6 Based on the derived comprehensive concordance/discordance index ${\Phi }^{p},$ it is easily seen that ${P}^{*}={\underset{p=1}{\mathrm{max}}}^{6}\left\{{\Phi }^{p}\right\}={K}_{1}.$

Namely, the ranking order of the three potential suppliers is: ${A}_{1}\succ {A}_{2}\succ {A}_{3}$. Therefore, the best alternative is ${A}_{1}$, while the worst is ${A}_{3}$

6 Comparative analysis and discussions

In this subsection, we present a comparative study to confirm the results of the developed N-QUALIFLEX method. In the neutrosophic environment, different discussion spaces have been defined, whose basic elements are single-valued neutrosophic sets, interval neutrosophic sets, single-valued neutrosophic hesitant fuzzy sets and so on, and many decision-making approaches have been presented based on the discussion spaces. However, as mentioned in section of Introduction, these approaches fail to handle the MCGDM problems in which the initial evaluations of alternatives on criteria are expressed by SVNNs and the values after aggregation are the SVNHFNs. That is, they have not yet handled the cases where the aggregated values are the SVNHFNs while the initial preference values are in form of SVNNs. Against the studies based on single-valued neutrosophic information and single-valued neutrosophic hesitant fuzzy information, this study combines two information in the same decision-making method and fills this gap in the neutrosophic literature. Thus, the advantages of the intended method from a general point of view can be listed as follows.

• (1) It offers an approach that uses all of the evaluation data provided by the DM to avoid information loss, unlike existing information aggregation operators.

• (2) It defines a new concept called the neutrosophic hesitancy index to determine the degree of hesitancy of a SVNHFN.

• (3) It defines two new distance measures between SVNHFNs to overcome the shortcomings of existing distance measures.

• (4) It aims two new comparison approaches for SVNHFN, based on neutrosophic hesitancy index; the first extends the existing comparison method and the other uses the defined distance measures.

• (5) It applies the QUALIFLEX method to neutrosophic hesitant fuzzy environment and uses SVNNs for the criterion weights in order to obtain more realistic results in the decision-making process.

• (6) It is highly effective in solving some decision-making problems where the number of criteria significantly exceeds the number of alternatives and most current neutrosophic decision-making methods cannot manage the process.

7 Conclusions and future research directions

SVNHFS is a tool use to handle problems with uncertain, imprecise, incomplete and inconsistent information, which widely exist in scientific and engineering cases. In this paper, we have developed a N-QUALIFLEX method to solve MCGDM problems in which the initial performance values of alternatives on criteria and the weights of the criteria are SVNNs, and their aggregated values are expressed by SVNHFNs. To do this, we first have introduced the concept of neutrosophic hesitancy index to measure the degree of hesitancy for the SVNHFN; meanwhile by applying the neutrosophic hesitancy index in the SVNHFNs, we have proposed two novel distance measures for SVNHFNs. Moreover, we have presented two comparison approaches in which first is directly based on the neutrosophic hesitancy index, and the latter is used the proposed distance measures for SVNHFNs. Then, from the perspective of decision-making method, we have applied the QUALIFLEX approach to neutrosophic sets and have proposed the N-QUALIFLEX method handling MCGDM problems. Finally, to demonstrate the functionality of the developed method, we have aimed to solve a suitable supplier selection problem on antivirus mask selection for the COVID-19 pandemic.

The results show that the novel approach has the many of advantages. In future, we will try using the hesitancy index to the different domains, for instance, fault diagnosis, machine learning and medical diagnosis. There are several directions for future research. Firstly, this study considers the effect of hesitancy indexes of decision makers in our numerical example, while the interrelationships among criteria are ignored. In our future research, the method will be improved by tools such as FCM or Choquet integral to cover this deficiency. Secondly, in this study, a single decision-making method was applied. However, each decision-making approach TODIM, TOPSIS, VIKOR and so on in the literature has different advantages. Therefore, it will be interesting for future research to investigate the hybrid types that combines the developed method and other methods.