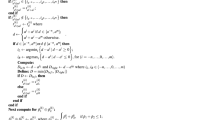Abstract
This paper aims to present a novel approach for computing two-player constant-sum matrix games laid on the notion of a “symbolic proportional” linguistic term set. It is not always possible to lay assessments based on uniformly and symmetrically distributed linguistic term sets; hence, the defined concept motivates the decision-makers to represent their opinions using 2-tuples composed of two proportional linguistic terms. The proportional 2-tuple linguistic representation of payoffs concerns linguistic labels, which do not certainly have to be symmetrically distributed or do not have the conventional prerequisite of having uniform distance among them. This representation confers an opportunity to describe the linguistic payoffs of a matrix game using members of a continuous linguistic scale domain. In our work, we have defined a two-player constant-sum proportional linguistic matrix game and proposed an approach of Proportional Linguistic Linear Programming (PLLP) to evaluate these game problems. The framed PLLP problem is then transformed into a crisp LPP that can be easily solved, decreasing the computation complexities involved in solving the linguistic decision-making problems. This perspective of proportional 2-tuples provides decision-makers an approach to represent their opinions not by just using one label, rather by proportional linguistic labels of the form \((\delta u_i,\,\gamma u_{i+1})\), where \(u_i\) and \(u_{i+1}\) are two successive linguistic terms, with \(0\le \delta ,\,\gamma \le 1\) and \(\delta \,+\,\gamma \,=\,1\). Besides, some test examples are also presented to show the consistency of our designed approach. Further, the PLLP formulation is utilized to solve a Multi-Criteria Decision-Making problem based on actual-time linguistic data.



Similar content being viewed by others
References
Abchir MA, Truck I (2013) Towards an extension of the \(2\)-tuple linguistic model to deal with unbalanced linguistic term sets. arXiv:1304.5897v1 : 1-17
Alonso S, Pérez IJ, Herrera-Viedma E (2008) A consensus model for group decision making unbalanced fuzzy linguistic contexts. XIV Congreso Español sobre Tecnologías y Lógica fuzzy : 449-456
Arfi B (2006) Linguistic fuzzy-logic game theory. J Conf Resol 50(1):28–57
Arfi B (2006) Linguistic fuzzy-logic social game of cooperation. Rational Soc 18(4):471–537
Barron EN (2011) Game theory: an introduction. Wiley, New Jersey
Bartczuk L, Dziwiński P, Starczewski JT (2012) A new method for dealing with unbalanced linguistic term set. ICAISC 2012 Part I. LNCS 7267:207–212
Bauso D (2016) Game theory with engineering applications. Advances in design and control, philadelphia: SIAM
Bector CR, Chandra S (2005) Fuzzy mathematical programming and fuzzy matrix games. Springer, Berlin
Bector CR, Chandra S, Vijay V (2004) Duality in linear programming with fuzzy parameters and matrix games with fuzzy payoffs. Fuzzy sets and systems 146:253–269
Bector CR, Chandra S, Vijay V (2004) Matrix games with fuzzy goals and fuzzy linear programming duality. Fuzzy optimization and decision making 3:255–269
Benz A, Jȧger G, Rooij RV (2006) Game theory and pragmatics. Palgrave Studies in Pragmatics, Language and Cognition, pp 1–82
Butnariu D (1978) Fuzzy games: a description of the concept. Fuzzy Set Syst 1:181–92
Cai M, Gong Z (2017) Group decision making using distances between unbalanced linguistic assessments. Appl Soft Comput 67:613–624
Cai M, Gong Z, Yu X (2016) A method for unbalanced linguistic term sets and its application in group decision making. Int J Fuzzy Syst 19(3):671–682
Cai X, Zhao H, Shang S, Zhou Y, Deng W, Chen H, Deng W (2021) An improved quantum-inspired cooperative co-evolution algorithm with muli-strategy and its application. Expert Syst Appl 171. https://doi.org/10.1016/j.eswa.2021.114629
Campos L (1989) Fuzzy linear programming models to solve fuzzy matrix games. Fuzzy Sets Syst 32:275–289
Charilas DE, Panagopoulos AD (2010) A survey on game theory applications in wireless networks. Comput Netw 54(18):3421–3430
Chen YW, Larbani M (2006) \(2\)-person zero-sum game approach for fuzzy multiple attribute decision making problems. Fuzzy Sets Syst 157:34–51
Delgado M, Verdegay JL, Vila MA (1990) Playing matrix games defined by linguistic labels. Multiperson decision making models using fuzzy sets and possibility theory, theory and decision library (Series B: Mathematical and Statistical Methods) 18 Springer, Dordrecht
Dengfeng L (1999) A fuzzy multi-objective programming approach to solve fuzzy matrix games. J Fuzzy Math 7(4):907–912
Deng W, Shang S, Cai X, Zhao H et al (2021a) Quantum differential evolution with cooperative coevolution framework and hybrid mutation strategy for large scale optimization. Knowledge-Based Systems 224(107080):1–14. https://doi.org/10.1016/j.knosys.2021.107080
Deng W, Shang S, Cai X, Zhao H, Song Y, Xu J (2021) An improved differential evolution algorithm and its application in optimization problem. Soft Comput. https://doi.org/10.1007/s00500-020-05527-x
Deng W, Xu J, Gao XZ, Zhao H (2020) An enhanced MSIQDE algorithm with novel multiple strategies for global optimization problems. IEEE Trans Syst Man Cybernet Syst. https://doi.org/10.1109/TSMC.2020.3030792
Deng W, Xu J, Zhao H, Song Y (2020) A novel gate resource allocation method using improved PSO-based QEA. IEEE Trans Intell Transp Syst. https://doi.org/10.1109/TITS.2020.3025796
Dong YC, Xu YF, Yu S (2009) Computing the numerical scale of the linguistic term set for the \(2\)-tuple fuzzy linguistic representation model. IEEE Trans. Fuzzy Syst. 17:1366–1378
Herrera F, Martínez L (2000) A \(2\)-tuple fuzzy linguistic representation model for computing with words. IEEE Trans Fuzzy Syst 8(6):746–752
Herrera F, Martínez L (2001) The \(2\)-tuple linguistic computational model, advantages of its linguistic description, accuracy and consistency. Int J Uncert Fuzz Knowl Based Syst 09:33–48
Herrera F, Martínez L (2001) A model based on linguistic \(2\)-tuples for dealing with multigranular hierarchical linguistic contexts in multi-expert decision making. IEEE Trans. Syst. Man. Cybern. B 31:227–234
Herrera F, Viedma EH, Martínez L (2008) A fuzzy linguistic methodology to deal with unbalanced linguistic term sets. IEEE Trans Fuzzy Syst 16(2):354–370
Jaeger G, Applications of game theory in linguistics. Lang Linguist Comp 2(3) : 406–421
Jiang YP, Fan ZP, Ma J (2008) A method for group decision making with multigranularity linguistic assessment information. Inf. Sci. 178:1098–1109
Malhotra T, Gupta A, Singh A (2019) Methodology for interval-valued matrix games with \(2\)-tuple fuzzy linguistic information. International Conference on Numerical Computations: Theory and Algorithms Springer, Cham : 154-168
Mazalov V (2014) Mathematical game theory and applications. Wiley, New Jersey
Neumann JV, Morgenstern O (1944) Theory of games and economic behavior. Princeton University Press, New York
Parthasarathy T, Raghavan TES (1971) Some topics in two-person games. American Elsevier Pub. Co., New York
Pei Z, Zheng L (2016) New unbalanced linguistic scale sets: the linguistic information representations and applications. Comput Indus Eng 105:377–390
Sahoo L (2017) Solving matrix games with linguistic payoffs. Int J Syst Assur Eng Manag 10(4):484–490
Singh H (1999) Introduction to game theory and its application in electric power markets. IEEE Comput Appl Power 12(4):18–20
Singh A, Gupta A (2018) Matrix games with interval-valued \(2\)-tuple linguistic information. Games 9(3):62
Singh A, Gupta A, Mehra A (2018) Matrix games with \(2\)-tuple linguistic information. Ann Oper Res 287:895–910
Song Y, Wu D, Mohamed AW, Zhou X, Zhang B, Deng W (2021) Enhanced success history adaptive de for parameter optimization of photovoltaic models. Complexity 6660115:1–22. https://doi.org/10.1155/2021/6660115
Straffin PD Jr (2010) Game theory and strategy. Math Assoc Am 36
Vijay V, Chandra S, Bector CR (2005) Matrix games with fuzzy goals and fuzzy payoffs. Omega 33(5):425–429
Vijay V, Mehra A, Chandra S, Bector CR (2005) Fuzzy matrix games via a fuzzy relation approach. Fuzzy Opt Dec Mak 6:299–314
Wang JH, Hao J (2006) a new version of \(2\)-tuple fuzzy linguistic representation model for computing with words. IEEE Trans Fuzzy Syst 14(3):435–445
Wang B, Liang J, Qian Y (2015) A Normalized numerical scaling method for the unbalanced multi-granular linguistic sets. Int J Uncert Fuzz Knowl Based Syst 23(2):221–243
Zadeh LA (1974) The concept of a linguistic variable and its application to approximate reasoning. Learning Systems and Intelligent Robots : 1-10, Boston
Zadeh LA (1965) Fuzzy Sets. Inf Control 8:338–353
Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning- II. Inf Sci 8(4):301–357
Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning- III. Inf Sci 9(1):43–80
Zaichenko H (2020) Fuzzy cooperative games of two players under uncertainty conditions. IEEE 2nd International Conference on System Analysis & Intelligent Computing (SAIC) : 1-6. https://doi.org/10.1109/SAIC51296.2020.9239214
Zou L, Pei Z, Karimi HR, Shi P (2012) The Unbalanced Linguistic Aggregation Operator in Group Decision Making. IEEE International Symposium on Intelligent Control (ISIC) : 703-707
Funding
This research received no external funding.
Author information
Authors and Affiliations
Contributions
Parul Chauhan is a research scholar in the Department of Applied Mathematics, Delhi Technological University under the supervision of Anjana Gupta. Parul Chauhan has designed the algorithm and prepared the manuscript in the present form with the guidance of Anjana Gupta.
Corresponding author
Ethics declarations
Conflict of Interest
Authors declare that they have no conflict of interest.
Ethical Approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Chauhan, P., Gupta, A. Matrix games with proportional linguistic payoffs. Soft Comput 25, 15067–15081 (2021). https://doi.org/10.1007/s00500-021-06363-3
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-021-06363-3