1 Introduction

Recently we have witnessed the rapid spread of the COVID-19 coronavirus around the world, appearing initially in China and then spreading to neighboring Korea and Japan, and after that to Europe, America and later Africa. In particular, in the case of Europe, Italy, Spain, France and Germany have been hit hard with the spread of the COVID-19 virus, having to this moment many confirmed cases and deaths. After that, in the American continent, the USA has also been hit hard with the spread of the COVID-19 virus. So, it is very crucial that decisive and strong research work is undertaken for understanding all the facets of this problem. This will help in being able to deal with its complexity and at the same time limit its negative impact on the health of the population around the globe and also minimizing the economic implications for the countries.

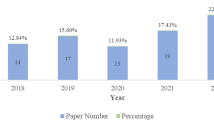
Due to the importance of finding ways to control the propagation of the virus, many papers (more than 1000 since January of this year) have been put forward on these past months related to different aspects of this problem. However, only about 50 papers deal with prediction, and less than that using artificial intelligence (like, neural networks). As an example, we can find only 13 papers related to COVID-19 prediction in the Web of Science database. In Fig. 1, we can find a distribution of these 13 papers according to the particular area in which the prediction task was applied. Of course, prediction is a very important task in being able to take actions for preventing bad consequences of COVID-19 propagation around the world. Good predictions are helpful in making good decisions at all levels of the governments.

Fig. 1
figure 1

Papers on COVID-19 prediction distributed according to their area

Full size image

As related work in the COVID-19 prediction, we can mention the following works. In Chen et al. (2020), the authors outline the prediction of the SARS-CoV-2 (2019-nCoV) 3C-as a protease structure. In Fan et al. (2020), the authors show an approach for the prediction of epidemic spread of the coronavirus driven by the spring festival transportation in China. In Goh et al. (2020), the authors discuss the rigidity of the outer shell predicted by a protein intrinsic disorder model with this uncovering COVID-19 (Wuhan-2019-nCoV) infectivity. In Grifoni et al. (2020), a bioinformatics approach that can predict candidate targets for immune responses to SARS-CoV-2 was presented. In He (2020), the author discusses what further could be done to control COVID-19 outbreaks in addition to the usual measures of isolation and contact tracing. In Huang et al. (2020), a spatial–temporal distribution of COVID-19 in China and its prediction was described. In Ibrahim et al. (2020), the authors describe the COVID-19 spike-host cell receptor GRP78 binding site prediction. In Ivanov (2020), an approach for predicting the impact of epidemic outbreaks on global supply chains with a simulation-based analysis on the coronavirus outbreak case was presented. In Li et al. (2020a, b), the authors describe the propagation analysis and prediction of the COVID-19. In Li et al. (2020a, b), the authors describe a forecasting method for the COVID-19 outbreak in China. In Liu et al. (2020), the authors report the understanding of unreported cases in the COVID-19 epidemic outbreak in Wuhan, China, and the importance of public health interventions. In Roda et al. (2020), the authors discuss why it is difficult to accurately predict the COVID-19 epidemic. In Roosa et al. (2020), the authors describe real-time forecasts of the COVID-19 epidemic in China from February 5th to February 24th, 2020. In Ton et al. (2020), the authors describe the rapid identification of potential inhibitors of SARS-CoV-2 main protease by deep model docking of 1.3 billion compounds. In Wang et al. (Wang et al. 2020), the authors describe a phase-adjusted estimation of the number of coronavirus Disease cases in Wuhan, China. In Zhang et al. (2020), the authors describe the estimation of the reproductive number of novel coronavirus (COVID-19) and the probable outbreak size on the Diamond Princess Cruise ship. In Zhou et al. (2020), a preliminary prediction of the basic reproduction number of the Wuhan novel coronavirus 2019 was presented. In all these previous related works, we can notice that only simple neural networks or deep neural models have been used. However, in this work we are proposing a new hybrid prediction model that combines modular and ensemble architectures of neural networks. In addition, the basic modules are based on nonlinear autoregressive neural networks. Simulation results of the proposed hybrid model are very good when compared with other approaches. In summary, the new prediction model is the main contribution of the paper.

The paper is organized as follows. Section 2 describes the basic concepts about nonlinear autoregressive neural networks. Section 3 describes the proposed hybrid method combining the modular and ensemble architectures of neural networks. Section 4 shows the simulation results. Section 5 contains a discussion of results. Finally, Sect. 6 offers the conclusion.

2 Nonlinear autoregressive neural networks

The Nonlinear Autoregressive Neural Network (NAR) model uses past values of the time series to predict future values. The NAR architecture consists of one input layer, one or more hidden layers and one output layer. The NAR is a dynamic and recurrent network with feedback connections (Sarkar et al. 2019). The NAR can be used in one-step ahead or multi-step ahead time series forecasting. The NAR model can be expressed mathematically as expressed in the following Eq. 1:

$$ y\left( t \right) = F\left( {y\left( {t - 1} \right),y\left( {t - 2} \right), \ldots ,y\left( {t - d} \right)} \right) $$
(1)

where \( y\left( t \right) \) is the value of the considered time series \( y \) at time \( t \), \( d \) is the time delay and \( F \) denotes the transfer function (Le et al. 2020). In Fig. 2, the NAR neural network architecture is illustrated in more detail.

Fig. 2
figure 2

The general architecture of the NAR neural network

Full size image

Artificial neural networks are a well-stablished methodology helping solve complicated problems (Leon et al. 2012; Norgaard et al. 2000). The artificial neural networks such as the NAR neural network are naturally used for time series forecasting due to their structure. The NAR has been used in many different areas, for example, it has been applied to generate multi-step ahead forecasts for the hourly solar radiation time series (Benmouiza and Cheknane 2013), multi-step ahead forecasts for wind power plant owners operating in a competitive energy market (Ahmed and Khalid 2017), in financial time series such as for crude oil prices (Safari and Davallou 2018) and forecasting of nitrogen dioxide (Yadav et al. 2019). Due to previous successful mentioned works, we decided to apply the NAR neural network to predict 5 days ahead for 11 countries of the world with the confirmed, recovered and death cases of the COVID-19. We decided to do this by using architecture of one hidden layer, the Levenberg–Marquardt backpropagation (trainlm) as the training function and 3 feedback time delays. The world dataset from the Humanitarian Data Exchange (HDX) website (2019) was used for producing the forecasts. However, in this paper the NAR model is only used as a simple module (of many) forming an ensemble, and then many ensemble predictors form the modular neural network for combining the results of the ensembles. In this way, achieving a better and more efficient prediction for all the countries around the world.

3 Proposed method

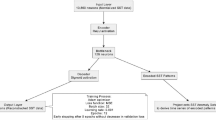
In this section, the proposed method is presented in more detail. In Fig. 3, we show the hybrid ensemble modular neural network approach, which combines a set of nonlinear autoregressive neural networks. In this figure, we have a modular neural architecture in the general model (at the top level), but each module of this architecture is in turn an ensemble neural model. In Fig. 3, we can note that each country has one module, and the outputs (predictions) are combined in an integrator to obtain improved predictions of the countries.

Fig. 3
figure 3

The general architecture of the hybrid modular ensemble prediction model

Full size image

The modules inside the architecture in Fig. 3 are ensemble neural models, which are formed by a set of NAR neural networks, as shown in Fig. 4.

Fig. 4
figure 4

Architecture modules, which are the ensemble models using NAR neural networks

Full size image

In summary, the ensemble of Fig. 4 is composed by a set of NAR neural networks (in this case, one for each country in the study) and the aggregator at the end joints all the individual predictions of the countries. We have to say that the proposed model in this paper was inspired in our previous works on modular neural networks and ensemble networks, as in Soto et al. (2014, 2019), Melin et al. (2012a, b), Sánchez et al. (2020).

4 Simulation results

In this section, the simulation results obtained with the proposed method are presented. The Covid-19 dataset used for training is from 01-22-2020 to 10-27-2020, and the detailed error analysis for the comparison of the proposed method is performed using the MSE, RMSE and Relative RMSE as shown in Tables 1, 2 and 3. We show in Fig. 5 the confirmed cases and the prediction from 01-22-2020 to 11-01-2020 for Belgium, China, France and Germany. We also show in Fig. 6 the confirmed cases and the prediction from 01-22-2020 to 11-01-2020 for Iran, Italy, Mexico and Spain.

Table 1 Prediction error values of confirmed cases of the neural model
Full size table
Table 2 Prediction error values of death cases of the neural model
Full size table
Table 3 Prediction error values of recovered cases of the neural model
Full size table
Fig. 5
figure 5

Confirmed cases and prediction of Covid-19 (a) in Belgium, (b) in China, (c) in France and (d) in Germany

Full size image
Fig. 6
figure 6

Confirmed cases and prediction of Covid-19 (a) in Iran, (b) in Italy, (c) in Mexico and (d) in Spain

Full size image

We show in Fig. 7 the confirmed cases and the prediction from 01-22-2020 to 11-01-2020 for Turkey, United Kingdom, United States and Worldwide. We also show in Fig. 8 the death cases and the prediction from 01-22-2020 to 11-01-2020 for China, Italy, Mexico and Spain.

Fig. 7
figure 7

Confirmed cases and prediction of Covid-19 (a) in Turkey, (b) in United Kingdom, (c) in United States and (d) Worldwide

Full size image
Fig. 8
figure 8

Death Cases and prediction of Covid-19 (a) in China, (b) in Italy, (c) in Mexico and (d) in Spain

Full size image

We show in the following Figures the Worldwide Covid-19 for all cases and prediction from 01-22-2020 to 11-01-2020. In Fig. 9, we show the death cases and prediction of Covid-19 Worldwide. In Fig. 10, we show the recovered cases.

Fig. 9
figure 9

Death cases and prediction of Covid-19 Worldwide

Full size image
Fig. 10
figure 10

Recovered cases and prediction of Covid-19 Worldwide

Full size image

As a way to validate the prediction accuracy of the proposed model, we show in the following Tables the prediction error values of the confirmed cases (Table 1), death cases (Table 2) and recovered cases (Table 3) for a sample 11 countries and the whole world. We used as testing set, 5 periods of time that the neural networks have not seen (in other words, the networks were trained with previous historical data, but tested with the unseen data). We are showing the Mean Squared Error (MSE), Root Mean Squared Error (RMSE) and relative RMSE, and this last value is the most representative since it can be interpreted as a percentage of error. For example, in Table 1 we can find that the prediction error for Belgium is about 4.87%, and for Mexico is 0.08%. The highest error for the countries is for France, which is 6.03%, but most of them are very good. And the prediction for the whole world we have about a 0.37% of error.

In Table 2, we can find that the prediction errors for death cases for Spain are about 1.45%, and for Turkey is 0.03%. The highest error for the countries is for Germany, which is 2.10%, for all of them are very good (lower than 3%). And the prediction for the whole world we have about a 0.06% of error, this is due to the approximating power of the hybrid model. We also show in Fig. 11 a pictorial representation of the distribution of deaths with respect to the countries.

Fig. 11
figure 11

Distribution of prediction errors in death cases with respect to the countries

Full size image

In Table 3, we can find that the prediction error of recovered cases for a set of 11 countries and for the whole world. In this case, as an example, for Germany is about 5.48%, and for Italy is 2.29%. The highest error for the countries is for the Belgium, which is 8.91%, but most of them are very good. And the prediction for the whole world is very good and we have about a 1.06% of error.

5 Discussion of results

In summary, the proposed method shows the highest error for Belgium in the recovered cases, which is 8.91%, for France in the confirmed cases having an error of 6.03%, for Germany in the death cases having and error of 2.10%. We can notice that for Belgium, Germany and Italy the prediction is more difficult in the confirmed, death and recovered cases. On the other hand, we can say that the proposed approach produces good prediction results and consequently we can recommend its use in real-world problems. Having analyzed the achieved results with the proposed method, we can definitely state that the hybrid approach presented in this paper can have relevance and importance in accurately predicting, both at the levels of countries and the world, the COVID-19 time series. The accurate prediction of this time series can lead to making the appropriate decisions for fighting the Pandemic at all levels, with this achieving a benefit for society and also for the economies of the world.

6 Conclusions

We have outlined in this paper a new approach for predicting the COVID-19 time series for the countries in the world using a hybrid modular ensemble neural network, which combines nonlinear autoregressive neural networks. At the top level of the modular neural network (MNN), the modules composing the MNN are ensembles designed to be efficient predictors for each country. In this case, an integrator (gating network) is used to combine the outputs of the modules, in this way achieving the goal of predicting the time series for a set of countries. At the level of the ensembles, these are constituted by a set of nonlinear autoregressive neural networks that are designed to be efficient predictors under particular conditions for each country. In each ensemble, the results of the modules are combined with an aggregator (minimum error) to achieve a better and improved result. Publicly available datasets of coronavirus cases around the globe, from the last months, have been used in the analysis. Simulation results show the effectiveness of the proposed hybrid modular ensemble neural network. Interesting conclusions have been obtained regarding the precision of the forecast based on the real data, which could be helpful in deciding on the best strategies for dealing with this virus for all countries in their fight against the coronavirus pandemic. In addition, the proposed approach could be helpful in proposing similar strategies for dealing with this virus in similar countries.

As future work, regarding the proposed hybrid modular ensemble neural network we envision that the integrator and aggregator need special attention and we plan to consider using type-2 fuzzy systems and the Sugeno integral to improve the results, as in the works Melin et al. (2007),( 2012a, b), Melin and Sánchez (2018), Sánchez et al. (2017). We also plan to combine our method with recent proposed prediction approaches using fuzzy logic and the fractal dimension, like in Melin et al. (2020a, b).