Skip to main content
SpringerLink
Log in

Numerical simulations of Newtonian fluid flow through a suddenly contracted rectangular channel with two different types of baffle plates

  • Methodologies and Application
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

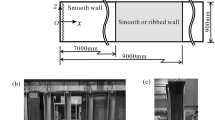
Numerical analysis of turbulent air flow structure through a rectangular channel along with multiple and different types of baffle plates has been performed, which is an important issue for heat exchangers and for that the flow characteristics and pressure drop are need to be identified. Finite Volume Method are employed to solve the governing equations using FLUENT with the Standard \(k-\epsilon \) turbulence model. The present study has been validated at \(\text {Re}=87{,}300\) with the studies of Dermitini et al. The aim of this study is to investigate the dynamic behavior of turbulent air flow, baffle height, baffle thickness and arrangement of baffle in different locations for high values of \(\text {Re}=88{,}000\). Moreover, flow structure and pressure drop characteristics are discussed in the presence of trapezoidal and plane shape baffles. Normalized velocity profiles and skin friction coefficients have been studied at different locations for trapezoidal and plane baffle plates. Finally, it has been concluded that pressure drop attains its maximum value at the upstream of the channel and minimum value at the downstream of the channel for both the plane and trapezoidal shape baffles. It is ensured that in trapezoidal case axial velocity is higher than plane baffle when four baffles are alternately placed at lower and upper walls. Furthermore, it has also been revealed that the separation of boundary layer is influenced by baffle height (h) and baffle thickness (b). At \(x=0.170 \ \mathrm{m}\), normalized velocity profiles \((u/u_{0})\) are presented for wide range of Reynolds number, \(\text {Re}\in [44{,}000-176{,}000]\) to reveal that increase of \(\text {Re}\) causes the increase in vortexes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  • Al-Atabi MT, Chin SB, Luo XY (2005) Visualization of mixing of the flow in circular tubes with segmental baffles. J Vis 8(2):89–92

    Article  Google Scholar 

  • Al-Atabi MT, Chin SB, Luo XY (2005) Flow structure in circular tubes with segmental baffles. J Vis Image Process 12:301–311

    Article  Google Scholar 

  • Bazdidi F, Naderi M (2004) Numerical analysis of laminar heat transfer in entrance region of a horizontal channel with transverse fins. Int Commun Heat Mass Trans 31:211–220

    Article  Google Scholar 

  • Bergelin OP, Brown GA, Colburn AP (1953) Heat transfer and fluid friction during flow across banks of tubes-V: a study of a cylindrical baffles exchanger without internal leakage. ASME J Heat Trans 75:841–850

    Google Scholar 

  • Berner C, Durst F, McEligot DM (1984) Flow around baffles. J Heat Trans 106:743–749

    Article  Google Scholar 

  • Demartini CL, Vielmo AH, Müller VS (2004) Numeric and experimental analysis of the turbulent flow through a channel with baffle plates. J Braz Soc Mech Sci Eng 26(2):153–159

    Article  Google Scholar 

  • Gay B, Williams TA (1968) Heat transfer on the shell-side of a cylindrical shell-and-tube heat exchanger fitted with segmental baffles. Trans Inst Chem Engrs 46:95–100

    Google Scholar 

  • Gay B, Mackley NV, Jenkins JD (1976) Heat transfer in baffled cylindrical shell-and-tube exchangers: an electrochemical transfer modelling technique. Int J Heat Mass Trans 19(9):995–1002

    Article  Google Scholar 

  • Gay B, Jenkins JD, Mackley NV (1977) Shell-side heat transfer coefficient in cylindrical heat exchangers: the influence of geometrical factors, I. The Leakage Case Lett Heat Mass Trans 4:41–52

    Article  Google Scholar 

  • Gay B, Jenkins JD, Mackley NV (1981) Shell-sided heat transfer coefficients in cylindrical heat exchangers: the influence of geometrical factors, II. The Leakage Case, Lett Heat Mass Trans 8:437–452

    Article  Google Scholar 

  • Gooray AN, Watkins GB, Aung W (1985) Turbulent heat transfer computations for rearward facing steps and sudden pipe expansions. ASME J Heat Trans 107:70–76

    Article  Google Scholar 

  • Gunter AY, Sennstrom HR, Kopp S (1947) A study of flow patterns in baffled heat exchangers. ASME 47-A-103

  • Habib MA, Durst F, McEligot DM (1984) Streamwise-Periodic flow around baffles, In: Proceeding of the 2nd International Conference on Applications of Laser Anemometry to Fluid Mechanics. pp. 1-6

  • Habib MA, Attya AE, McEligot DM (1988) Calculation of turbulent flow and heat transfer in channels with streamwise-periodic flow. ASME J Turbomach 110:405–411

    Article  Google Scholar 

  • Habib MA, Mobarak AM, Sallak MA, Hadi EA, Affify RI (1994) Experimental investigation of heat transfer and flow over baffles of different heights. J Heat Trans 116:1609–1617

    Article  Google Scholar 

  • Hwang RR, Chow YC, Peng YF (1999) Numerical study of turbulent flow over two-dimensional surface-mounted ribs in a channel. Int J Numer Methods Fluids 37:767–785

    Article  Google Scholar 

  • Ichimiya K (1987) Effects of several roughness elements on an insulated wall for heat transfer from the opposite smooth heated surface in a parallel plate duct. ASME J Heat Trans 109:68–73

    Article  Google Scholar 

  • Kang K, Anand NK (2003) Use of porous baffles to enhance heat transfer in a rectangular channel. Int J Heat Mass Trans 46(22):4191–4199

    Article  Google Scholar 

  • Kelkar KM, Patankar SV (1987) Numerical prediction of flow and heat transfer in a parallel plate channel with staggered fins. J Heat Trans 109:25–30

    Article  Google Scholar 

  • Knudsen WW, Katz DL (1958) Fluid Dynamics and Heat Transfer. McGraw-Hill, New York

    MATH  Google Scholar 

  • Launder EB, Spalding BD (1974) The numerical computation of turbulent flow. Comput Methods Appl Mech Eng 3(2):269–289

    Article  Google Scholar 

  • Mehdi SQ, Mushatet SK (2008) Simulation of turbulent flow and heat transfer through a duct with baffle plates. J Eng Dev 12(3):142–157

    Google Scholar 

  • Molki M, Mostoufizadeh RA (1989) Turbulent heat transfer in rectangular ducts with repeated-baffle blockages. Int J Heat Mass Trans 32(8):1491–1499

    Article  Google Scholar 

  • Nasiruddin MH, Kamran S (2007) Experimental study of turbulent flows through pipe bends. Int J Heat Fluid Flow 28:318–328

    Article  Google Scholar 

  • Patankar SV, Liu CH, Sparrow EM (1977) Fully developed flow and heat transfer in ducts having streamwise-periodic variations of cross-sectional area. J Heat Trans 99(2):180–186

    Article  Google Scholar 

  • Prashanta D, Akram H (2005) Internal cooling augmentation in rectangular channel using inclined baffle plates. Int J Heat Fluid Flow 26:799–816

    Google Scholar 

  • Prithiviraj M, Andrews MJ (1988) Three dimensional numerical simulation of shell and tube heat exchangers. J Numer Heat Trans 33(6):799–816

    Google Scholar 

  • Rajendra K, Maheshwarib BK, Nitin K (2005) Experimental study of heat transfer enhancement in an asymmetrically heated rectangular duct with perforated baffles. Int Commun Heat Mass Trans 32(2):275–284

    Google Scholar 

  • Shivani T, Gajusingh A, Nasiruddin S, Kamran S (2010) The impact of a vortex induced by a baffle on the turbulent structure. Exp Therm Fluid Sci 34:590–602

    Article  Google Scholar 

  • Vogel JC, Eaton JK (1985) Combined heat transfer and fluid dynamic measurements downstream of a Backward–Facing step. ASME J Heat Trans 107:922–929

    Article  Google Scholar 

  • Webb BW, Ramadhyani S (1985) Conjugate heat transfer in a channel with staggered ribs. Int J Heat Mass Trans 28(9):1679–1687

    Article  Google Scholar 

  • Webb GW, Ramadhyani S (1985) Fluid flow and heat transfer in a parallel plate channel with staggered baffles. J Heat Mass Trans 28(5):471–495

    Google Scholar 

  • Wiemer P (1937) Untersuchung über den Zugwiederstand von Wasserrohrkesseln, Dissertation, RWTH Aachen

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, NIT, Silchar, Assam, 788010, India

    Sandip Saha, Pankaj Biswas & Lokendra Singh

  2. Department of Mechanical Engineering, NIT, Silchar, Assam, 788010, India

    Sujit Nath

Authors
  1. Sandip Saha
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pankaj Biswas
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sujit Nath
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Lokendra Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pankaj Biswas.

Ethics declarations

Conflict of interest

Mr. Sandip Saha is a PhD scholar of NIT Silchar in the Department of Mathematics and he has received research grants from MHRD. Dr. Pankaj Biswas is an assistant professor of NIT Silchar in the Department of Mathematics. Dr. Sujit Nath is an assistant professor of NIT Silchar in the Department of Mechanical Engineering. Mr. Lokendra Singh is a Msc 2nd year student of NIT Silchar in the Department of Mathematics.

Ethical standard

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Saha, S., Biswas, P., Nath, S. et al. Numerical simulations of Newtonian fluid flow through a suddenly contracted rectangular channel with two different types of baffle plates. Soft Comput 25, 9873–9885 (2021). https://doi.org/10.1007/s00500-020-05326-4

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-020-05326-4

Keywords

Search

Navigation