Evolutionary optimization of artificial neural network using an interactive phase-based optimization algorithm for chaotic time series prediction

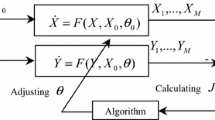
Abstract

The prediction of chaotic time series is an important issue in nonlinear information procession. Due to the multi-modal, high-dimensional and non-differentiable or discontinuous characteristics of chaotic systems, global optimization techniques are required to avoid from falling into local optima for the prediction of chaotic time series. Phase-based optimization is recently proposed as a global search algorithm inspired by natural phenomena. In this paper, an improved phase-based optimization algorithm integrating stochastic interaction strategy and global optimal interaction strategy, termed interactive phase-based optimization (IPBO), is proposed to train feed-forward neural networks (FNNs) for chaotic time series prediction. The combination of stochastic interaction strategy and global optimal interaction strategy can balance the capability of exploration and exploitation in the global optimization process. To demonstrate the searching capability, sixteen widely used benchmark functions are firstly used to investigate its optimization performance. Then, the prediction effectiveness of FNNs trained by IPBO has been illustrated using classical chaotic time series of Lorenz, Box–Jenkins and Mackey–Glass. The training and testing performances of IPBO and other state-of-the-art optimization algorithms have been compared for predicting these time series. Conducted numerical experiments indicate that IPBO is not only competitive in functions optimization and has also a better learning ability in training FNNs among other state-of-the-art optimization algorithms.