1 Introduction

The electricity available to consumers requires three basic steps: generation, transmission, and distribution. Those involve two markets: energy market and transmission service market. Both markets are operated under a monopoly of the past. To avoid the dependence on a single supply region, which brings the ineffectiveness of electricity market, the electricity systems currently are restructuring or going to restructure in several countries. This process has different paradigms, leading to different ways to develop electricity models for the power market. One way which attracts considerable attention is modeling through Nash equilibria. As far as we are concerned, there are mainly three approaches to model the spatial oligopolistic electricity market by Nash equilibria. One is the supply function equilibrium model, see references (Bolle 1992; Green and Newbery 1992; Klemperer and Meyer 1989). Another is the Bertrand equilibrium model, please refer to Hobbs and Kelly (1992). The third is the Cournot equilibrium model, see (Borenstein and Bushnell 1996; Oren 1997; Schmalensee and Golub 1984).

Historically speaking, researchers studied either the long-run equilibria or the short-term equilibria of those models. For instance, Wei and Smeer (1999) looked at a long-term spatial oligopolistic electricity equilibrium model. Fehr and Harbord (1993) investigated a short-run supply function equilibrium model of the electricity in the UK. Smeers and Wei (1997) discussed different short-run equilibria on the electricity power market. All work we mentioned above only focused on a static situation. However, the electricity market involves some indeterminancies in reality. For instance, not only some unexpected weather condition like hurricanes, tornadoes, etc., but also some natural disasters like floods, seaquakes, earthquakes, etc., even some emergencies like train crashes and rumors will influence the power demands in a region. To cope with the indeterminancies, Pineau and Murto (2003) considered a dynamic stochastic oligopolistic model of multi-market segments (the demand growth rate of the supply was modeled as a stochastic variable) and applied it to the Finnish electricity market.

However, the indeterminancy lying the nature and society does not confine to the randomness. Beside randomness, there is another type of indeterminancy–uncertainties. Here “Uncertainties”, as a jargon, come from the uncertainty theory, which is a branch of mathematics to deal with indeterminancies and concerned with the analysis of belief degree (Please refer to Liu 2019). The belief degree appeared here describes to what degree someone believes an event will happen under the case that there is no sample or very few samples to derive from what is studied. For example, it is difficult to know the exact oil reserves in a region. For an oil company, there is no choice but to invite some experts to estimate and give their belief degrees to the quantities of the oil underground. Then the oil company will decide whether to bid the oilfield according to the analysis of experts’ belief degrees.

Inspired by the aforementioned studies, this paper mainly investigates a single-period spatial oligopolistic electricity model, regarding the electricity demand as an uncertain variable. The case we study only involves the generation and the transmission of electricity. All producers compete for supplying the electricity to consumers in the Cournot manner, and the transmission service is provided by a transmission company. All producers aim at maximizing their profits under some uncertain factors. Profit, in this situation, has no conceptual meaning. We maximize uncertain profits of producers in the sense of optimistic values. That is the bigger the optimistic value of a producer’s uncertain profit is, the larger profit a producer earns.

The present paper is constructed as follows. Some basic concepts and lemmas in uncertainty theory are covered in Sect. 2. A single-period spatial oligopolistic electricity model with uncertain demands is given in Sect. 3. The description of the single-period spatial oligopolistic electricity model with uncertain demands is described in Sect. 3.1 while its formulation into a variational inequality is presented in Sect. 3.2. An illustrative example is constructed in Sect. 4. We conclude our work in Sect. 5. Appendix discusses the \(\beta -\)optimistic/pessimistic value of a crisp number, which is a special uncertain variable in uncertainty theory.

2 Preliminary

In this section, we recall some basics in uncertainty theory, which is a new branch of mathematics founded by Liu (2007) in 2007.

Let \(\varGamma \) be a nonempty set and let \({\mathcal {L}}\) be a \(\sigma -\)algebra on it. We call the ordered pair \((\varGamma ,\mathcal {L})\) a measurable space. The members of \({\mathcal {L}}\) are measurable sets in \(\varGamma ,\) which are also renamed as events in uncertainty theory. Liu (2004) defined an uncertain measure on \((\varGamma ,{\mathcal {L}})\) to describe the belief degree with which a person believes an event \(\varLambda \) may happen. It is a set function \({\mathcal {M}}\) defined on the measurable space \((\varGamma ,\mathcal {L})\) which satisfies the following three axioms:

Axiom 1 (Normality Axiom) \({\mathcal {M}}(\varGamma )=1\) for the universal set \(\varGamma .\)

Axiom 2 (Duality Axiom) \(\mathcal {M}\{\varLambda \}+{\mathcal {M}}\{\varLambda ^{c}\}=1\) for any event \(\varLambda .\)

Axiom 3 (Subadditivity Axiom) For every countable sequence of events \(\varLambda _1,\varLambda _2,\ldots ,\) we have

$$\begin{aligned} {\mathcal {M}}\left\{ \bigcup _{i=1}^{\infty }\varLambda _i\right\} \leqslant \displaystyle \sum _{i=1}^{\infty }\mathcal {M}\{\varLambda _i\}. \end{aligned}$$

The triplet \((\varGamma , {\mathcal {L}},{\mathcal {M}})\) is called an uncertainty space. It is one vital concept in uncertainty theory. Another one is the uncertain variable used to represent the quantity of uncertainty. An uncertain variable is a function \(\xi \) from an uncertainty space \((\varGamma ,{\mathcal {L}},{\mathcal {M}})\) to the set of real numbers such that \(\{\xi \in B\}=\{\gamma \in \varGamma |\;\xi (\gamma )\in B\}\) is an event for any Borel set B. Uncertain variables \(\xi _1,\xi _2,\ldots ,\xi _n\) are said to be independent if \({\mathcal {M}}\left\{ \bigcap _{i=1}^{n}(\xi _i\in B_i)\right\} =\bigwedge _{i=1}^{n}{\mathcal {M}}\{\xi _i\in B_i\}\) for any Borel sets \(B_1,B_2,\ldots ,B_n\) of real numbers. The uncertainty distribution \(\varPhi (t)\) of an uncertain variable \(\xi \) is defined via \(\varPhi (t)={\mathcal {M}}\{\xi \leqslant t\}\) for any real number t. If \(\varPhi (t)\) is continuous, then \({\mathcal {M}}\{\xi \geqslant t\}=1-\varPhi (t)\). The function \(\varPhi (t)\) is said to be regular if it is continuous and strictly increasing with respect to t at which \(0<\varPhi (t)<1,\) and \(\displaystyle \lim _{t\rightarrow -\infty }\varPhi (t) =0,\displaystyle \lim _{t\rightarrow +\infty }\varPhi (t)=1.\) The inverse function \(\varPhi ^{-1}(\alpha )\) of \(\varPhi (t)\) for \(\alpha \in [0,1]\) is called the inverse uncertainty distribution of \(\xi .\)

We now present what we need to use in the sequel.

Definition 1

(Liu 2014) An uncertain variable \(\xi \) is called linear if it has a linear uncertainty distribution

$$\begin{aligned} \varPhi (t)= {\left\{ \begin{array}{ll} 0, &{} \;\text{ if }\;\; t\leqslant a,\\ \dfrac{t-a}{b-a},&{}\;\text{ if }\;\; a\leqslant t\leqslant b,\\ 1, &{}\;\text{ if }\;\;t\geqslant b, \end{array}\right. } \end{aligned}$$
(1)

denoted by \({\mathcal {L}}(a,b),\) where a and b are real numbers with \(a<b.\)

Definition 2

(Liu 2004) An uncertain variable \(\xi \) is called normal if it has a normal uncertainty distribution

$$\begin{aligned} \varPhi (t)=\left( 1+\exp \left( \frac{\pi (e-t)}{\sqrt{3} \sigma }\right) \right) ^{-1},\;t\in R, \end{aligned}$$
(2)

denoted by \({\mathcal {N}}(e,\sigma ),\) where e and \(\sigma \) are real numbers with \(\sigma >0.\)

Remark 1

  1. (1)

    An uncertain variable \(\xi \) with linear uncertainty distribution \({\mathcal {L}}(a,b)\) has an inverse uncertainty distribution

    $$\begin{aligned} \varPhi ^{-1}(\alpha )=(1-\alpha )a+\alpha b. \end{aligned}$$
  2. (2)

    An uncertain variable \(\xi \) with normal uncertainty distribution \({\mathcal {N}}(e,\sigma )\) has an inverse uncertainty distribution

    $$\begin{aligned} \varPhi ^{-1}(\alpha )=e+\dfrac{\sqrt{3}\sigma }{\pi }\ln \dfrac{\alpha }{1-\alpha }, \alpha \in (0,1). \end{aligned}$$
    (3)

Definition 3

(Liu 2007) Let \(\xi \) be an uncertain variable, and \(\beta \in (0,1]\). Then

$$\begin{aligned} \xi _{\sup }(\beta )=\sup \{r|{\mathcal {M}}\{\xi \geqslant r\}\geqslant \beta \} \end{aligned}$$

is called the \(\beta -\)optimistic value to \(\xi ;\) and

$$\begin{aligned} \xi _{\inf }(\beta )=\inf \{r|{\mathcal {M}}\{\xi \leqslant r\}\geqslant \beta \} \end{aligned}$$

is called the \(\beta -\)pessimistic value to \(\xi \).

The following conclusions can be drawn from definitions of linear uncertainty distribution, normal uncertainty distribution, \(\beta \)-optimistic/pessimistic values and Remark 1.

Let \(\xi \sim {\mathcal {L}}(a,b)\) with the uncertainty distribution \(\varPhi ,\) then

$$\begin{aligned} \begin{aligned} \xi _{\sup }(\beta )&=\varPhi ^{-1}(1-\beta )=\beta a+(1-\beta ) b, \\ \xi _{\inf }(\beta )&=\varPhi ^{-1}(\beta )=(1-\beta )a+\beta b. \end{aligned} \end{aligned}$$
(4)

If \(\xi \sim {\mathcal {N}}(e,\sigma )\) with the uncertainty distribution \(\varPhi ,\) then

$$\begin{aligned} \begin{aligned} \xi _{\sup }(\beta )&=\varPhi ^{-1}(1-\beta )=e-\dfrac{\sqrt{3}\sigma }{\pi }\ln \dfrac{\alpha }{1-\alpha },\\ \xi _{\inf }(\beta )&=\varPhi ^{-1}(\beta )=e+\dfrac{\sqrt{3}\sigma }{\pi }\ln \dfrac{\alpha }{1-\alpha }. \end{aligned} \end{aligned}$$
(5)

Furthermore, \(\beta -\)optimistic/pessimistic values share the properties as follows.

Lemma 1

(Chen [3] and Liu 2010) Suppose that \(\xi \) and \(\eta \) are independent uncertain variables. Then for any \(\beta \in (0,1],\) we have

$$\begin{aligned} \begin{aligned} (\xi +\eta )_{\sup }(\beta )&=\xi _{\sup }(\beta )+\eta _{\sup }(\beta ), \\ (\xi +\eta )_{\inf }(\beta )&=\xi _{\inf }(\beta )+\eta \,_{\inf }(\beta ),\\ (\xi \cdot \eta )_{\sup }(\beta )&=\xi _{\sup }(\beta )\cdot \eta _{\sup }(\beta ),\\ (\xi \cdot \eta )_{\inf }(\beta )&=\xi _{\inf }(\beta )\cdot \eta \,_{\inf }(\beta ) \;\text{ if }\;\;\xi \geqslant 0,\eta \geqslant 0,\\ (\lambda \xi )_{\sup }(\beta )&=\lambda \xi _{\sup }(\beta ),\\ (\lambda \xi )_{\inf }(\beta )&=\lambda \xi _{\inf }(\beta )\;\text{ if }\; \lambda \geqslant 0,\\ (\lambda \xi )_{\sup }(\beta )&=\lambda \xi _{\inf }(\beta ), (\lambda \xi )_{\inf }(\beta )=\lambda \xi _{\sup }(\beta )\;\text{ if }\;\lambda <0. \end{aligned} \end{aligned}$$

Lemma 2

(Liu 2003) A function \(\varPhi ^{-1}(\alpha ): (0,1)\)\(\rightarrow R\) is an inverse uncertainty distribution if and only if it is continuous and strictly increasing with respect to \(\alpha .\)

Lemma 3

(Liu 2014) Let \(\xi _1,\xi _2,\ldots ,\xi _n\) be uncertain variables, g a real-valued measurable function. Then \(g(\xi _1,\xi _2,\ldots ,\xi _n)\) is an uncertain variable. If \(\xi _1,\xi _2,\ldots ,\xi _n\) are independent of each other, and \(g_{1},g_{2},\ldots ,g_{n}\) are measurable functions, then \(g_{1}(\xi _{1}),g_{2}(\xi _{2}),\ldots ,g_{n}(\xi _{n})\) are also independent uncertain variables.

Lemma 4

(Liu 2014) Let \(\xi \) be an uncertain variable with uncertainty distribution \(\varPhi (t),\) and let g(y) be a strictly decreasing function with respect to y. Then \(g(\xi )\) has an uncertainty distribution

$$\begin{aligned} \varPsi (t)=1-\varPhi (g^{-1}(t)), \end{aligned}$$
(6)

where \(g^{-1}(t)\) is the inverse function of g(y).

3 Main discussion

3.1 Problem description

We describe in this part a single-period spatial oligopolistic electricity model under uncertain demands. The generators are assumed to behave in the Cournot manner. The relevant notions are introduced first as a preliminary to define strategies and equilibria of this game.

\(I=\{1,\ldots ,i,\ldots ,n\}{:}\) Set of generation firms in the market.

\(J=\{1,\ldots ,j,\ldots ,m\}{:}\) Set of nodes of the network.

\(G_{ij}{:}\) Set of generation plant types ( for example, hydro power plant, thermal power plant, nuclear power plant, pumped storage power plant, etc.) owned by firm i in region j.

\(s_{ij}{:}\) Power supplied by firm i to region j.

\(s_{j}=\sum _{i\in I}s_{ij}{:}\) Total power supplied in region j.

\(p_{j}(s_{j},\xi _{j}){:}\) Uncertain inverse demand function of energy in region j,  where the uncertain variable \(\xi _{j}\) is an uncertain factor.

\(q_{k}{:}\) Electricity produced by plant \(k\in G_{ij}.\)

\(C_{k}(q_{k}){:}\) Production cost function of plant k.

\({\bar{q}}_{k}{:}\) Generation capacity at plant k.

\(f_{i,(j,j')}{:}\) Power generated by firm i and sent from node j through transmission capacity \((j, j\,')\) to node \(j\,'.\)

\(\bar{f}_{(j,j')}{:}\) Transmission capacity on link \((j,j\,').\)

\(\rho _{_{(j,j')}}{:}\) Transmission price through capacity \((j, j\,').\)

\(\varvec{\rho }\)\(=(\rho _{_{(j,j\,')}}\geqslant 0:(j,j\,')\in A){:}\) Vector of prices for transmission services, where A is the set of electric transmission capacities in the network.

Thus, the strategy set for each producer can now be introduced. Assume that all producers play the game in a noncooperative manner. Both of the strategy set and the payoff function of a producer depend on the other producers’ strategies. Consequently, the equilibrium of this spatial oligopolistic model is a generalized Nash equilibrium.

For simplicity, we denote

$$\begin{aligned} {\varvec{x}}_{i}=\left( \begin{array}{ll} s_{ij} &{}:j\in J\\ q_{k}&{}:k\in G_{ij}\\ f_{i,(j,j')}&{}:(j,j')\in A \end{array} \right) \end{aligned}$$
(7)

as producer i’s decision vector. Additionally, let \({\varvec{x}}_{-i}=({\varvec{x}}_{i'}:i'\ne i)\) be the decision vector of all firms but i.

The constraints that must be satisfied by \({\varvec{x}}_{i}\) are as follows:

  1. 1.

    The energy flow has a bound. That is the flow in each link \((j,j')\in A\) is less than or equal to the available transmission capacity.

  2. 2.

    The power output of each plant is limited. That is to say, the generation level is less than or equal to the available generation capacity for each plant.

  3. 3.

    The power in any region keeps balance. That is the flow, the generation and the supply of the power are balanced at each node.

When fixed \({\varvec{x}}_{-i}\), we denote \(K_{i}({\varvec{x}}_{-i})\) as firm i’s feasible set satisfied all above-mentioned constraints. That is

$$\begin{aligned} K_{i}({\varvec{x}}_{-i})=\left\{ \begin{array}{ll} &{}q_{k}\leqslant {\bar{q}}_{k},\forall \;k\in G_{ij},\forall j\in J,\\ {\varvec{x}}_{i}\geqslant 0:&{}s_{ij}+\sum \nolimits _{(j,j')\in A}f_{i,(j,j')}=\\ &{}\sum \nolimits _{ k\in G_{ij}}q_{k} +\sum \nolimits _{(j',j)\in A}f_{i,(j,j')},\\ &{}\forall j\in J\\ &{}f_{i,(j,j\,')}-f_{i,(j\,',j)}+f_{i^{-},(j,j\,')}\\ &{}-\,f_{i^{-},(j\,',j)}\leqslant \bar{f}_{(j,j')} \end{array}, \right\} \end{aligned}$$

where \(f_{i^{-},(j,j')}=\sum _{i'\ne i}f_{i',(j,j\,')}\). Note that firm i’s feasible set \(K_{i}({\varvec{x}}_{-i})\) depends on other firms’ decision variables through the following capacity constraint:

$$\begin{aligned} f_{i,(j,j\,')}-f_{i,(j\,',j)}+f_{i^{-},(j,j\,')} -f_{i^{-},(j\,',j)}\leqslant \bar{f}_{(j,j\,')} \end{aligned}$$
(8)

Let \({\varvec{x}}=({\varvec{x}}_{i}:i\in I)\) be the vector of all firms’ decision variables. Then firm i’s uncertain profit function equals its uncertain revenue minus its generation cost and transmission cost:

$$\begin{aligned} \theta _{i}({\varvec{x}},\varvec{\xi }_{i})&=\sum \nolimits _{j=1}^{m}s_{ij}p_{j}(s_{j}, \xi _{j})-\sum \nolimits _{j=1}^{m}\sum \nolimits _{k\in G_{ij}}C_{k}(q_{k})\nonumber \\&\quad -\,\sum \nolimits _{(j,j\,')\in A}\rho _{_{(j,j\,')}}\cdot f_{i,(j,j\,')}. \end{aligned}$$
(9)

Note that \(\theta _{i}({\varvec{x}},\varvec{\xi }_{i})\) depends on other firms’ strategies only through the demand variables \(s_{i'j}\) with \(i'\ne i\) in \(s_{j}\).

In this paper, we attempt to use the \(\beta -\)optimistic value criterion to study the equilibrium in the electricity power market. This leads to solve the following optimization problem: fixed \({\varvec{x}}_{-i},\) which is composed of other firms’ decision variables, and the transmission price vector \(\varvec{\rho },\) solve the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \text{ maximize }\; \theta _{i}({\varvec{x}},\varvec{\xi }_{i})_{\sup }(\beta )\\ \text{ subject } \text{ to }\; {\varvec{x}}_{i}\in K_{i}(x_{-i}), \end{array}\right. } \end{aligned}$$
(10)

for all \(i\in I\), where \(\beta \) is a given confidence level in (0, 1). For simplicity, we denote problem (10) as \(\beta -OPT({\varvec{x}}_{-i},\varvec{\rho })\). The overall equilibrium of this model is to solve each \(\beta -OPT({\varvec{x}}_{-i},\varvec{\rho })\) for all \(i\in I,\) which is further denoted as problem \(\beta -OPT.\) When solving the uncertain profit maximization problem under the criterion of \(\beta -\)optimistic value, we treat other firms’ decision variables and transmission prices as endogenous.

Now we present the formal definition of the equilibrium of this spatial oligopolistic electricity market.

Definition 4

The equilibrium of the spatial oligopolistic electricity market with the Cournot generators under uncertain demands by the criterion of \(\beta -\)optimistic value is to find a point

$$\begin{aligned} {\varvec{x}}^{*}_{i}=(s^{*}_{ij},q^{*}_{h},f^{*}_{i,(j,j\,')}:j\in J,k\in G_{ij},(j,j\,')\in A),i\in I, \end{aligned}$$

and a set of transmission prices

$$\begin{aligned} \varvec{\rho }^{*}=\varvec{\rho }(f^{*}), \end{aligned}$$

where \(f^{*}=(\sum _{i\in I}f^{*}_{i,(j,j\,')}:(j,j\,')\in A),\) such that \({\varvec{x}}^{*}_{i}\) solves the problem \(\beta -OPT({\varvec{x}}^{*}_{-i},\varvec{\rho }^{*})\) for all \(i\in I.\)

In other words, the overall equilibrium problem of this spatial oligopolistic electricity market is to seek a vector \({\varvec{x}}^{*}=({\varvec{x}}^{*}_{i}:i\in I)\) such that \({\varvec{x}}^{*}_{i}\) solves \(\beta -OPT({\varvec{x}}^{*}_{-i},\varvec{\rho })\) for each i and \(\rho ^{*}_{_{(j,j\,')}}\) for all \((j,j\,')\in A.\) Obviously, producer i’s strategy is dependent on other producers’ through constraint (8). It is this dependence that has the implication for the interpretation of the model in terms of game theory. As mentioned previously, it also implies that the equilibrium introduced in Definition 4 is a generalized Nash equilibrium.

3.2 Problem formulation

In this section, we formulate the model of \(\beta -OPT\) as a single variational inequality problem. To this end, we formulate the optimization problem \(\beta -OPT({\varvec{x}}_{-i},\varvec{\rho })\) first. Note that it is naturally a quasi-variational inequality problem because of the dependence of the set \(K_{i}({\varvec{x}}_{-i})\) on \({\varvec{x}}_{-i}\) for any i. The special structure of the producers’ strategy sets leads to reformulate the problem \(\beta -OPT({\varvec{x}}_{-i},\varvec{\rho })\) into a variational inequality problem. The whole process consists of two phases. One is recasting the objective function \(\theta _{i}({\varvec{x}},\varvec{\xi }_{i})_{\sup }(\beta );\) the other is reformulating the feasible set \(K_{i}({\varvec{x}}_{-i}).\) We deal with them one by one.

We handle \(\theta _{i}({\varvec{x}},\varvec{\xi }_{i})_{\sup }(\beta )\) first. Recall that the uncertain profit for firm i is

$$\begin{aligned} \begin{aligned} \theta _{i}({\varvec{x}},\varvec{\xi }_{i})&=\sum _{j=1}^{m}s_{ij}p_{j}\,(s_{j}, \xi _{j})-\sum _{j=1}^{m}\sum _{k\in G_{ij}}C_{k}(q_{k})\\&\quad -\,\sum _{(j,j')\in A}\rho _{_{(j,j\,')}}f_{i,(j,j\,')}\\&\quad \triangleq \sum _{j=1}^{m}s_{ij}p_{j}\,(s_{j},\xi _{j}) -\triangle ^{1}-\triangle ^{2}, \end{aligned} \end{aligned}$$

where \(\triangle ^{1}=\sum _{j=1}^{m}\sum _{k\in G_{ij}}C_{k}(q_{k}),\)\(\triangle ^{2}=\sum _{(j,j')\in A}\rho _{_{(j,j\,')}}f_{i,(j,j\,')}.\)

From the point of uncertainty theory, we need the following assumptions on uncertain variables.

Assumption 1

The uncertain variable \(\xi _{j},j\in J \) in the uncertain inverse demand function \(p_{j}(s_{j},\xi _{j})\) has a regular uncertainty distribution \(\varPhi _{j}\) and the function \( p_{j}\,(s_{j},\xi _{j})\) is decreasing on \(\xi _{j}\) for each \(j\in J.\) Furthermore, all uncertain variables \(\xi _{j},j\in J\) are independent of each other.

Theorem 1

Suppose that \(\xi _{j}\) and \( p_{j}\,(s_{j},\xi _{j})\) satisfy Assumption 1, then we have

$$\begin{aligned} \theta _{i}({\varvec{x}},\varvec{\xi }_{i})_{\sup }(\beta )&=\sum \nolimits _{j=1}^{m}s_{ij} p_{j}\,(s_{j},\varPhi ^{-1}_{j}(\beta ))\nonumber \\&\quad -\,\sum \nolimits _{j=1}^{m}\sum \nolimits _{k\in G_{ij}}C_{k}(q_{k})\nonumber \\&\quad -\,\sum \nolimits _{(j,j')\in A}\rho _{_{(j,j\,')}}f_{i,(j,j\,')}. \end{aligned}$$
(11)

Proof

Since the \(\beta \)-optimistic value of \(\xi \) is \(\varPhi ^{-1}(1-\beta )\) when \(\xi \) has an inverse uncertainty distribution \(\varPhi ,\) it is easy to obtain Theorem 1 with the help of Lemma 4. \(\square \)

Remark 2

  1. 1)

    By the same token, the \(\beta -\)pessimistic value of \( \theta _{i}({\varvec{x}},\varvec{\xi }_{i})\) is

    $$\begin{aligned} \begin{aligned} \theta _{i}({\varvec{x}},\varvec{\xi }_{i})_{\inf }(\beta )&=\sum _{j=1}^{m}s_{ij}p_{j} \,(s_{j},\varPhi ^{-1}_{j}(1-\beta ))\\&\quad -\, \sum _{j=1}^{m}\sum _{k\in G_{ij}}C_{k}(q_{k})\\&\quad -\,\sum _{(j,j')\in A}\rho _{_{(j,j\,')}}f_{i,(j,j\,')}. \end{aligned} \end{aligned}$$
  2. 2)

    We can also derive both the \(\beta -\)optimistic and \(\beta -\)pessimistic value of \( \theta _{i}({\varvec{x}},\varvec{\xi }_{i})\) when \(p_{j}\,(s_{j},\xi _{j})\) is increasing on \(\xi _{j}\) for each \(j\in J\) similarly.

For convenience, when given \(\beta \in (0,1),\) we denote \(p_{j}\,(s_{j},\varPhi ^{-1}_{j}(\beta ))\triangleq \bar{p}_{j}\,(s_{j},\beta ),\)\(\theta _{i}({\varvec{x}},\varvec{\xi }_{i})_{\sup }(\beta )={{\tilde{\theta }}}_{i}({\varvec{x}},\beta ).\)

Up till now, we had formulated the objective function in the problem \(\beta -OPT({\varvec{x}}_{-i},\varvec{\rho })\) to be a function which only involves the decision variable \({\varvec{x}}\) and the confidence level \(\beta .\) Before we push our discussion further, in conformity with the generally accepted economic behavior, we present some assumptions as follows:

Assumption 2

  1. 1)

    For all \(\beta \in (0,1),\)\(j\in J,\) every \(\bar{p}_{j}\,(s_{j},\beta )\) has the following characteristics:

    1-1:

    $$\begin{aligned} \bar{p}_{j}(s_{j},\beta )= {\left\{ \begin{array}{ll} \geqslant 0,&{} s_{j}\in (0,S_{j}),\\ =0,&{}s_{j}\geqslant S_{j}, \end{array}\right. } \end{aligned}$$

    where \(S_{j}\) is a constant.

    1-2: \(\bar{p}_{j}\,(s_{j},\beta )\) is strictly decreasing and continuously twice differentiable with respect to \(s_{ij}.\)

  2. 2)

    For all \(j\in J,\)\(\beta \in (0,1),\) the associated revenue function \(s_{ij}\bar{p}_{j}(s_{j},\beta )\) is strictly concave on \(s_{ij},\) where \(s_{j}=\sum _{i\in I}s_{ij}.\)

Assumption 3

For all \(i\in I, j\in J, k\in G_{ij},\) each cost function \(C_{k}(q_k)\) is convex and twice continuously differentiable with respect to \(q_k.\)

Murphy et al. (1982) had shown that Assumptions 2 and 3 imply the following result.

Lemma 5

When given \(\beta \in (0,1),\)\(s_{ij}\bar{p}_{j}(s_{ij}+\bar{S},\beta )\) is concave on \(s_{ij}\) for \(0\leqslant \bar{S}\leqslant S_{j}-s_{ij}\) and \(0\leqslant \bar{S}.\)

As a result of all Assumptions and Lemma 5, when given \(\beta \in (0,1),\) the objective function \({{\tilde{\theta }}}_{i}({\varvec{x}},\beta )\) is continuously differentiable and concave on \({\varvec{x}}.\)

We next turn to formulate the feasible set \(K_{i}({\varvec{x}}_{-i})\) of firm i. To this end, let

$$\begin{aligned} {\tilde{K}}_{i}=\left\{ \begin{array}{ll} {\varvec{x}}_{i}\geqslant 0:&{}\quad q_{k}\leqslant {\bar{q}}_{k},\forall \;k\in G_{ij},\forall j\in J,\\ &{} s_{ij}+\sum \nolimits _{(j,j')\in A}f_{i,(j,j')}=\sum \nolimits _{ k\in G_{ij}}q_{k}\\ &{}+\sum \nolimits _{(j',j)\in A}f_{i,(j,j')},\forall j\in J \end{array} \right\} . \end{aligned}$$

Note that \({\tilde{K}}_{i}\) is independent of \({\varvec{x}}_{-i},\) that is, \({\tilde{K}}_{i}\) only involves the decision variable of firm i. Hence, \({\tilde{K}}_{i}\cap {\tilde{K}}_{i'}=\emptyset \) whenever \(i\ne i'.\) Denote by \({\tilde{K}}_{i}({\varvec{x}}_{-i})\) the set of \({\varvec{x}}_{i}\) satisfying constraint (8), that is,

$$\begin{aligned} {\tilde{K}}_{i}({\varvec{x}}_{-i})=\left\{ \begin{array}{ll} {{\varvec{x}}}_{i}\geqslant 0&{}:f_{i,(j,j')}-f_{i,(j',j)}+f_{i^{-},(j,j')}\\ &{}\quad -\,f_{i^{-},(j',j)}\leqslant \bar{f}_{(j,j')} \end{array} \right\} . \end{aligned}$$

Thus, \({\tilde{K}}_{i}({\varvec{x}}_{-i})\) is a mapping of \({\varvec{x}}_{-i},\) which is the constraint imposed on producer i’s strategy through other producers’ strategies.

Let

$$\begin{aligned} \nabla _{{\varvec{x}}_{i}}{{\tilde{\theta }}}_{i}({\varvec{x}},\beta )=\left( \begin{array}{lc} MR_{i,j}(s_{ij},\beta ):&{}\forall \,\, j\\ -MC_{k}(q_{k}):&{}\forall \,\, k\\ -\rho (f):&{}(j,j')\in A \end{array} \right) , \end{aligned}$$
(12)

where \(MR_{ij}(s_{ij},\beta )=\dfrac{\partial {{\tilde{\theta }}}_{i}({\varvec{x}},\beta )}{\partial s_{ij}}\) denotes firm i’s marginal return in region j with a given confidence level \(\beta \in (0,1),\)\(MC_{k}(q_{k})=\dfrac{d C_{k}\big (q_{k}\big )}{d q_{k}}\) is its marginal cost at generation plant k. Here we recall that given a closed convex set \(K\in R^{n}\) and a continuous function \(F:K\rightarrow R^{n},\) the variational inequality defined by K and F (which is denote by VI(K, F)) means to find an \({\varvec{x}}^{*}\in K\) such that

$$\begin{aligned} ({\varvec{x}}-{\varvec{x}}^{*})^{T}F({\varvec{x}}^{*})\geqslant 0,\;\text{ for } \text{ all }\;{\varvec{x}}\in K. \end{aligned}$$

Now we go back to our problem. Let \(F({\varvec{x}},\beta )=(\nabla _{{\varvec{x}}_{i}}{{\tilde{\theta }}}_{i}({\varvec{x}},\beta ):i\in I)\) and \(K=(\prod _{i\in I}{{\tilde{K}}}_{i})\cap \bar{K},\) where

$$\begin{aligned} \bar{K}= & {} \left\{ {\varvec{x}}\geqslant 0:\sum _{i\in I}f_{i,(j,j\,')}-\sum _{i\in I}f_{i,(j\,',j)}\right. \\&\quad \left. \leqslant \bar{f}_{(j,j\,')},\forall (j,j\,')\right\} . \end{aligned}$$

We reveal the relation between the model \(\beta -OPT\) and the VI(K, F) in the theorem followed. And under what conditions can guaranteed the existence of a solution to the VI(K, F) are also presented.

Theorem 2

  1. (1)

    Suppose that Assumptions 1–3 hold. Then every solution to the VI(K, F) is an equilibrium of the model \(\beta -OPT.\) In other words, the vector \(( {\varvec{x}}^{*}, \varvec{\rho }^{*})\) is an equilibrium of \(\beta -OPT\) if \({\varvec{x}}^{*}\in K\) solves the VI(K, F),  which is

    $$\begin{aligned} \begin{aligned} ({\varvec{x}}^{*}-{\varvec{x}})^{T}F({\varvec{x}}^{*},\beta )&= \sum _{i\in I}({\varvec{x}}^{*}_{i}-{\varvec{x}}_{i})^{T}\nabla _{{\varvec{x}}_{i}} {{\tilde{\theta }}}_{i}({\varvec{x}}^{*},\beta )\\&\quad \geqslant 0,\;\;\; \text{ for } \text{ all }\;\;{\varvec{x}}\in K. \end{aligned} \end{aligned}$$
    (13)
  2. (2)

    Suppose that \(( {\varvec{x}}^{*}, \varvec{\rho }^{*})\) is an equilibrium of the model \(\beta -OPT\) and let \(\lambda ^{*}_{i,(j,j')}\) be a dual vector of constraint (8) of the problem \(\beta -OPT({\varvec{x}}^{*}_{-i},\varvec{\rho }^{*}).\) Then \({\varvec{x}}^{*}\) solves VI(K, F) if \( \lambda ^{*}_{i,(j,j')}=0\) for all \(i,(j, j').\)

  3. (3)

    Assume that Assumptions 1–3 hold, if \(\varvec{\rho }=\varvec{\rho }(f)\) is continuous, then there exists a solution to the VI(K, F) hence an equilibrium to \(\beta -OPT.\)

Proof

The proof of this theorem is essentially the same as its counterpart in Wei and Smeer’work (1999) except that there is a parameter \(\beta \) in the objective function, so it is omitted here. \(\square \)

Remark 3

The model \(\beta -OPT\) is equivalent to the VI(K, F) when the transmission price \(\varvec{\rho }(f^{*})\) is such that at all equilibria, \( \lambda ^{*}_{i,(j,j')}=0\) for all \(i,(j, j')\) from Theorem 2.

4 An application

To demonstrate what we discussed in the previous section, we present an application in this part.

4.1 Market assumptions

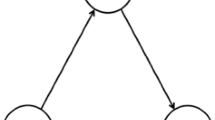
The market investigation here consists of two investor-owned electric utilities that supply electricity to two sectors: residential sector and commercial sector. Note that in order to correspond with the data we obtained, the electric utility will be used to take place of the power producer/firm in this subsection and the followed one. Figure 1 describes the network under investigation.

Fig. 1
figure 1

Network under investigation

Full size image

The dataFootnote 1 is from US Energy Information Administration mainly for the year 2015.

A linear uncertain inverse demand function is calibrated for each consumption sector. This can be done by computing the price elasticity at the reference prices and considering some indeterminant factors. The reference prices, in 2015, for the residential sector and commercial sector, respectively, are 0.1265 and 0.1064 USD/KWh. The total net generation by nuclear source and thermal source is 205,174,5 GWh. It is divided between the residential and commercial sectors with the ration 48/52 in this paper. Suppose that one electric utility has only the thermal power plants while the other owns only nuclear power plants. The average power plant operating expense for a thermal power plant is 25.71 while the average power plant operating expense for a nuclear power plant is 37.26 Mills/KWh, respectively. Note that \(1 \text{ Mill }=\dfrac{1}{1000} \text{ USD }\).

In this application, we assume that the total supply of the power is synonymous to the total production as well as the total flow. Denote the two electric utilities as \(U_1\) and \(U_2.\) The decision variable of \(U_{i}\) is \({\varvec{x}}_{i},\) which is further composed of \(x_{i1}\) and \(x_{i2}(i=1,2).\) Note that \(x_{ij}\) represents the power supplied by the utility \(U_{i}(i=1,2)\) to the sector \(j(j=1,2).\)

4.2 Computation and analysis

The linear uncertain inverse demand functions are computed from the price elasticity between the data of sales and the average price of electricity to ultimate customers for 2014–2015 together with uncertain variables. Here, the uncertain variable depicts some uncertain factors in the electricity power market. Those uncertainties are caused by a certain natural disasters such as hurricanes, tornadoes, seaquakes, earthquakes, etc., and the uncertain demands of consumption sectors.

The linear uncertain inverse demand function of the electricity power at sectors \(j_1,j_2\) are, respectively, represented by

$$\begin{aligned} p_{1}({\varvec{x}},\xi _1)=713{,}079.9804-0.4178(x_{11}+x_{21}+\xi _1), \end{aligned}$$

and

$$\begin{aligned} p_{2}({\varvec{x}},\xi _{2})=264{,}749.8419-0.1164(x_{12}+x_{22}+\xi _{2}), \end{aligned}$$

where \({\varvec{x}}=({\varvec{x}}_{1},{\varvec{x}}_{2})^{T}=((x_{11},x_{12})^{T},(x_{21},x_{22})^{T})^{T},\)\(\xi _{1}\) is a linear uncertain variable with the uncertainty distribution \({\mathcal {L}}(-100{,}100),\) while \(\xi _{2}\) is a normal uncertain variable with uncertainty distribution \({\mathcal {N}}(100,10).\) Moreover, \(\xi _{1}\) and \(\xi _{2}\) are independent of each other. Denote \(\varvec{\rho }=(\rho _{1},\rho _{2})^{T}\) as the transmission price vector, where \(\rho _{1}\) and \(\rho _{2}\) are the unit transmission prices delivered to two sectors. For convenience, the operating expense of the production is scaled up as USD/GWh, the consumption of the electricity power is weighted as GWh. Given the decision variable \({\varvec{x}}_{-1}={\varvec{x}}_{2}\) and the transmission price vector \(\varvec{\rho },\) the uncertain profit function of utility \(U_1\) is

$$\begin{aligned} \begin{aligned} \theta _{1}({\varvec{x}},\varvec{\xi })&=x_{11} p_{1}({\varvec{x}},\xi _1)+x_{12} p_{2}({\varvec{x}},\xi _2)\\&\quad -\,25{,}710(x_{11}+x_{12})\\&\quad -\,\rho _{1}x_{11}-\rho _{2}x_{12}\\&=x_{11}\cdot \left[ 687{,}369.9804-\rho _{1}\right. \\&\quad \left. -\,0.4178(x_{11}+x_{21}+\xi _1)\right] \\&\quad +\,x_{12}\cdot \left[ 227{,}477.4968-\rho _{2}\right. \\&\quad \left. -\,0.1164(x_{12} +x_{22}+\xi _2)\right] . \end{aligned} \end{aligned}$$

The corresponding constraint set is

$$\begin{aligned}&K_{1}({\varvec{x}}_{-1})=K_{1}({\varvec{x}}_{2})\\&\quad =\left\{ \begin{array}{ll} &{}x_{11}\geqslant 0,x_{12}\geqslant 0,\\ (x_{11},x_{12})^{T}:&{}x_{11}+x_{21}\leqslant 984{,}837.6,\\ &{}x_{12}+x_{22}\leqslant 1{,}066{,}907.4,\\ \end{array} \right\} . \end{aligned}$$

Then the problem \(\beta -OPT({\varvec{x}}_{-1},\varvec{\rho })\) with \(\beta =0.75\) for utility \(U_1\) is

$$\begin{aligned} {\left\{ \begin{array}{ll} \text{ maximize }\; \theta _{1}({\varvec{x}},\varvec{\xi })_{\sup }(0.75)\\ \text{ subject } \text{ to }\; {\varvec{x}}_{1}\in K_{1}(x_{-1}). \end{array}\right. } \end{aligned}$$

From the inverse uncertainty distributions of the linear and the normal uncertain variables, together with Theorem 1, it leads to the following result.

$$\begin{aligned} \begin{aligned}&\theta _{1}({\varvec{x}},\varvec{\xi })_{\sup }(0.75)\\&\quad =x_{11}\cdot \left[ 687{,}369.9804-0.4178\left( x_{11}+x_{21}\right. \right. \\&\qquad \left. \left. +250\right) -\rho _{1}\right] +x_{12} \cdot \left[ 227{,}489.8419\right. \\&\qquad -0.1164\left. \left( x_{12}+x_{22}+100\right. \right. \\&\qquad \left. \left. +\dfrac{10\sqrt{2}}{\pi }\ln 3\right) -\rho _{2}\right] \\&\quad =x_{11}\cdot \left[ 687{,}265.5304-0.4178\left( x_{11} +x_{21}\right) -\rho _{1}\right] \\&\qquad +x_{12}\cdot \left[ 227{,}477.4968-0.1164(x_{12}+x_{22}) -\rho _{2}\right] \\&\quad ={\tilde{\theta }}_{1}({\varvec{x}},0.75). \end{aligned} \end{aligned}$$

The gradient of \({\tilde{\theta }}_{1}({\varvec{x}},0.75)\) is

$$\begin{aligned} \nabla \tilde{\theta _{1}}({\varvec{x}},0.75)=(MR_{11}(x_{11},0.75)), MR_{12}(x_{12},0.75))^{T}, \end{aligned}$$

where

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}MR_{11}(x_{11},0.75)=\dfrac{\partial {{\tilde{\theta }}}_{1}(x,0.75)}{x_{11}}\\ &{}=687{,}265.5304-0.4178(2x_{11}+x_{12})-\rho _{1},\\ &{}MR_{12}(x_{12},0.75)=\dfrac{\partial {{\tilde{\theta }}}_{1}(x,0.75)}{x_{12}}\\ &{}=227{,}477.4968-0.1164(x_{11}+2x_{12})-\rho _{2},\\ \end{array}\right. } \end{aligned}$$
(14)

We do not intend to write down the uncertain profit function of utility \(U_2,\) its \(0.75-\)optimistic value \({\tilde{\theta }}_{2}({\varvec{x}},0.75),\) and its gradient \(\nabla {\tilde{\theta }}_{1}({\varvec{x}},0.75)\) because they can be reached analogously. Denote

$$\begin{aligned} {{\tilde{K}}}_1= & {} \{{\varvec{x}}_{1}=(x_{11},x_{12})^{T}:x_{1}\geqslant 0, \;\text{ i.e., }\; x_{11},x_{12}\geqslant 0\},\\ {{\tilde{K}}}_2= & {} \{{\varvec{x}}_{2}=(x_{21},x_{22})^{T}:x_{2}\geqslant 0, \;\text{ i.e., }\; x_{21},x_{22}\geqslant 0\},\\ \bar{K}= & {} \left\{ \begin{array}{ll} ({\varvec{x}}_{1},{\varvec{x}}_{2})^{T}: &{}x_{11}+x_{21}\leqslant 984{,}837.6,\\ &{}x_{12}+x_{22}\leqslant 1{,}066{,}907.4,\\ \end{array} \right\} . \end{aligned}$$

Let

$$\begin{aligned} K=(\tilde{K_1}\times \tilde{K_2})\cap \bar{K}. \end{aligned}$$

Denote \(F({\varvec{x}},0.75)=(\nabla {\tilde{\theta }}_{1}({\varvec{x}},0.75), \nabla {\tilde{\theta }}_{2}({\varvec{x}},0.75))^{T}, {\varvec{x}}=({\varvec{x}}_1,{\varvec{x}}_2)^{T},\) it follows from Theorem 2 that the variational inequality of \(0.75-OPT\) is to find an \({\varvec{x}}^{*}\in K\) such that

$$\begin{aligned} F({\varvec{x}}^{*},0.75)^{T}({\varvec{x}}^{*}-{\varvec{x}})\geqslant 0,\;\text{ for } \text{ all }\;{\varvec{x}}\in K. \end{aligned}$$

In other words, it is

$$\begin{aligned}&\nabla {\tilde{\theta }}_{1}({\varvec{x}}^{*},0.75)^{T}({\varvec{x}}_{1}^{*}-{\varvec{x}}_1) +\nabla {\tilde{\theta }}_{2}({\varvec{x}}^{*},0.75)^{T}({\varvec{x}}_{2}^{*}-{\varvec{x}}_2)\geqslant 0,\\&\quad \text{ for } \text{ all }\;x\in K, \end{aligned}$$

which is also

$$\begin{aligned} \sum _{i=1}^{2}\sum _{j=1}^{2}MR_{ij}(x_{ij}^{*},0.75)(x_{ij}^{*}-x_{ij})\geqslant 0 \;\text{ for } \text{ all }\;x_{ij}\in K.\nonumber \\ \end{aligned}$$
(15)

Furthermore, the variational inequality problem (15) is equivalent to the following linear programming problem:

$$\begin{aligned}&\max _{x_{ij}\geqslant 0,i,j=1,2} \quad MR_{11}(x_{11}^{*},0.75)x_{11}+ MR_{12}(x_{12}^{*},0.75)x_{12}\\&\qquad +MR_{21}(x_{21}^{*},0.75)x_{21}+MR_{22}(x_{22}^{*},0.75)x_{22} \end{aligned}$$

subject to

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}x_{11}+x_{21}\leqslant 984{,}837.6,\\ &{}x_{12}+x_{22}\leqslant 1{,}066{,}907.4.\\ \end{array}\right. } \end{aligned}$$
(16)

Let \(\lambda _{1},\lambda _{2}\) be the dual variables of the constraints above, then the corresponding dual problem of (16) is

$$\begin{aligned} \min _{\lambda _{1},\lambda _{2}\geqslant 0} \quad&984{,}837.6 \lambda _{1}+1{,}066{,}907.4\lambda _{2} \end{aligned}$$

subject to

$$\begin{aligned}&{\left\{ \begin{array}{ll} &{}\lambda _{1}-MR_{11}(x^{*}_{11},0.75)\geqslant 0,\\ &{}\lambda _{2}-MR_{12}(x^{*}_{12},0.75)\geqslant 0,\\ &{}\lambda _{1}-MR_{21}(x^{*}_{21},0.75)\geqslant 0,\\ &{}\lambda _{2}-MR_{22}(x^{*}_{22},0.75)\geqslant 0,\\ \end{array}\right. } \end{aligned}$$
(17)

The complementarity slackness implies that

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} \lambda _{1}=MR_{11}(x^{*}_{11},0.75)=MR_{21}(x^{*}_{21},0.75),\\ &{} \lambda _{2}=MR_{12}(x^{*}_{12},0.75)=MR_{22}(x^{*}_{22},0.75),\\ \end{array}\right. } \end{aligned}$$
(18)

for any solution \(x^{*}_{ij}>0,i,j=1,2.\)

It follows from (14) and its counterparts of the electric utility \(U_2,\) together with (18), that

$$\begin{aligned} \begin{aligned} x^{*}_{11}&=506{,}241.2031,x^{*}_{12}=583{,}067.1021,\\ x^{*}_{21}&=478{,}596.397,x^{*}_{22}=483{,}840.298. \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \lambda _{1}^{*}&=64{,}292.8065-\rho _{1},\\ \lambda _{2}^{*}&=35{,}408.8247-\rho _{2} \end{aligned} \end{aligned}$$
(19)

Let \(\lambda _{i}^{*}=0,i=1,2.\) It follows from the remark of Theorem 2 that the equilibrium prices of the corresponding transmission links are

$$\begin{aligned} \begin{aligned} \rho _{1}^{*}&=64{,}292.8065,\\ \rho ^*_{2}&=35{,}408.8247.\\ \end{aligned} \end{aligned}$$
(20)

Expression (20) reveals that the transmission prices of the residential and commercial sectors, respectively, are 64, 292.8065 and 35, 408.8247 USD/GWh. Both are close to the delivery prices 6.59, 4.38 Cents/KWh (that is 65, 900, 43, 800 USD/GWh) reported by the US Energy Information Administration. This application indicates that our model is not only effective but also can be used as a way to deal with the transmission pricing problem through a confidence level \(\beta \) under uncertainties.

5 Conclusion

We established in this paper a single-period spatial oligopolistic electricity model under uncertain demands. Since the profit of each firm is an uncertain variable, there is no conceptual solution to the uncertain profit maximization problem. To ensure there exists the conceptual solution, we used the optimistic value of the uncertain variable as an optimization criterion. We assumed that all producers compete with each other in the Cournot manner. Accordingly, all firms play a noncooperative game whose feasible sets are dependent on their rivals’ strategies because of the limited capacity in each transmission link. This generalized Nash equilibrium has a natural description of a quasi-variational inequality. However, it was recast to be a variational inequality in this paper due to the special structure of the feasible sets. An application was presented to show that the equilibrium of the electricity market under uncertain demands was the solution to the corresponding variational inequality through the electricity system of America. We only considered the case of the optimistic value criterion in this paper; however, we can also discuss other cases such as pessimistic value criterion, Hurwicz criterion and the expected value criterion. Those remain to be further work.