Skip to main content
SpringerLink
Log in

ANFIS-based model for predicting actual shear rate associated with wall slip phenomenon

  • Methodologies and Application
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

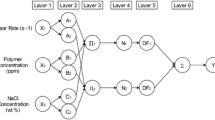
Wall slip can be defined as a phenomenon in the flow of suspensions due to the movement of particles away from the wall boundary, leaving a thin liquid rich layer adjacent to the wall. It should be taken into consideration in material designing, manufacturing and transportation as it may cause inaccurate rheological measurements such as shear rate and viscosity. The apparent (measured) shear rate is higher than the actual shear rate. The traditional method for actual shear rate determination is not efficient from the perspective of time and cost consumption. Therefore, there is a need to develop a mathematical model that is able to detect the complex pattern of the actual shear rate and accurately predict its value based on the available measured input variables. Volumetric concentration, particle size, temperature and shear stress are selected as the input, while the actual shear rate is kept as output while designing the architecture of ANFIS model. Sixteen ANFIS models with different architecture were designed and evaluated using different statistical indices. Model XVI with number of membership function equal to 3, input product of two sigmoid membership function, output linear membership function type integrated with hybrid optimization method appears to be the most suitable model architecture for predicting the actual shear rate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Ahuja A, Singh A (2009) Slip velocity of concentrated suspensions in Couette flow. J Rheol 53:1461–1485

    Article  Google Scholar 

  • Ali MZ, Reynolds RG (2014) Cultural algorithms: a Tabu search approach for the optimization of engineering design problems. Soft Comput 18:1631–1644

    Article  Google Scholar 

  • Arqub OA (2017) Adaptation of reproducing kernel algorithm for solving fuzzy Fredholm--Volterra integrodifferential equations. Neural Comput Appl 28:1591–1610

    Article  Google Scholar 

  • Arqub OA, AL-Smadi M, Momani S, Hayat T (2016) Numerical solutions of fuzzy differential equations using reproducing kernel Hilbert space method. Soft Comput 20:3283–3302

    Article  Google Scholar 

  • Arqub OA, Al-Smadi M, Momani S, Hayat T (2017) Application of reproducing kernel algorithm for solving second-order, two-point fuzzy boundary value problems. Soft Comput 21:7191–7206

    Article  Google Scholar 

  • Barnes HA (1995) A review of the slip (wall depletion) of polymer solutions, emulsions and particle suspensions in viscometers: its cause, character and cure. J Nonnewton Fluid Mech 56:221–251

    Article  Google Scholar 

  • Buscall R, McGowan J, Morton-Jones AJ (1993) The rheology of concentrated dispersions of weakly attracting colloidal particles with and without wall slip. J Rheol 37:621–641

    Article  Google Scholar 

  • Chen L, Duan Y, Zhao G, Liu M (2008) Effects of temperature, solid particle size and concentration on wall slip behaviour of coal-water slurry in pipelines. J Chem Ind Eng (China) 59:2206–2213

    Google Scholar 

  • Chin RJ, Lai SH, Shaliza I, Wan Zurina WJ (2018) Factors affect wall slip: particle size, concentration and temperature. Appl Rheol 28:15775-1-9

    Google Scholar 

  • Chin RJ, Lai SH, Shaliza I, Wan Zurina WJ, Ahmed Elshafie AH (2019a) New approach to mimic rheological actual shear rate under wall slip condition. Eng Comput 35:1409–1418

    Article  Google Scholar 

  • Chin RJ, Lai SH, Shaliza I, Wan Zurina WJ, Elshafie A (2019b) Rheological wall slip velocity prediction model based on artificial neural network. J Exp Theor Artif Intell 31:1–18

    Article  Google Scholar 

  • Cohen Y, Metzner AB (1982) Adsorption effects in the flow of polymer solutions through capillaries. Macromolecules 15:1425–1429

    Article  Google Scholar 

  • Cohen Y, Metzner AB (1986) An analysis of apparent slip flow of polymer solutions. Rheol Acta 25:28–35

    Article  Google Scholar 

  • Gulmus SA, Yilmazer U (2005) Effect of volume fraction and particle size on wall slip in flow of polymeric suspensions. J Appl Polym Sci 98:439–448

    Article  Google Scholar 

  • Howard D, Kolibal J, Brezulianu A (2011) Engineering presentation of the stochastic interpolation framework and its applications. Soft Comput 15:79–87

    Article  Google Scholar 

  • Jana SC, Kapoor B, Acrivos A (1995) Apparent wall slip velocity coefficients in concentrated suspensions of noncolloidal particles. J Rheol 39:1123–1132

    Article  Google Scholar 

  • Jang JS (1993) Adaptive network-based fuzzy inference system. IEEE Trans Syst Man Cybern 23:665–685

    Article  Google Scholar 

  • Jang JS, Sun CT (1997) Neuro-Fuzzy and soft computing: a computing approach to learning and machine intelligence. Prentice Hall, Englewood Cliffs

    Google Scholar 

  • Jang JS, Sun CT, Mizutani E (1997) A computational approach to learning and machine intelligence. Neuro-Fuzzy and Soft Computing. Prentice-Hall, Upper Saddle River

    Book  Google Scholar 

  • Kalyon DM (2005) Apparent slip and viscoplasticity of concentrated suspensions. J Rheol 61:621–640

    Article  Google Scholar 

  • Karaman S, Kayacier A (2011) Effect of temperature on rheological characteristics of molasses: modelling of apparent viscosity using adaptive neuro-fuzzy inference system (ANFIS). LWT Food Sci Technol 44:1717–1725

    Article  Google Scholar 

  • Khalilpourazari S, Khalilpourazary S (2019) An efficient hybrid algorithm based on water cycle and moth-flame optimization algorithms for solving numerical and constrained engineering optimization problems. Soft Comput 23:1699–1722

    Article  Google Scholar 

  • Khosla R, Li Q (2014) Unified problem modeling language for knowledge engineering of complex systems. Soft Comput 8:491–511

    Article  Google Scholar 

  • Korotkikh V, Korotkikh G (2008) On principles in engineering of distributed computing systems. Soft Comput 12:201–206

    Article  Google Scholar 

  • Malkin AY, Baranov AV, Vickulenkova ME (1993) Experimental estimation of wall slip for filled rubber compounds. Rheol Acta 32:150–155

    Article  Google Scholar 

  • Pérez-González J, López-Durán JJ, Marín-Santibáñez BM, Rodríguez-González F (2012) Rheo-PIV of a yield-stress fluid in a capillary with slip at the wall. Rheol Acta 51:937–946

    Article  Google Scholar 

  • Ponalagusamy R (2016) Particulate suspension Jeffrey fluid flow in a stenosed artery with a particle-free plasma layer near the wall. Korea-Aust Rheol J 28:217–227

    Article  Google Scholar 

  • Ponalagusamy R (2017) A two-layered suspension (particle-fluid) model for non-Newtonian fluid flow in a catheterized arterial stenosis with slip condition at the wall of stenosed artery. Korea-Aust Rheol J 29:87–100

    Article  Google Scholar 

  • Saad EI (2015) Axisymmetric motion of a spherical porous particle perpendicular to two parallel plates with slip surfaces. Can J Phys 93:784–795

    Article  Google Scholar 

  • Shaliza I, Wong SD, Baker IF, Zamzam Z, Sato M, Kato Y (2015) Influence of geometry and slurry properties on fine particles suspension at high loadings in a stirred vessel. Chem Eng Res Des 94:324–336

    Article  Google Scholar 

  • Soltani F, Yilmazer U (1998) Slip velocity and slip layer thickness in flow of concentrated suspensions. J Appl Polym Sci 70:515–522

    Article  Google Scholar 

  • Toker OS, Yilmaz MT, Karaman S, Dogan M, Kayacier A (2012) Adaptive neuro-fuzzy inference system and artificial neural network of apparent viscosity of ice-cream mixes stabilized with different concentrations of xanthan gum. Appl Rheol 22:63918-1-11

    Google Scholar 

  • Valdez MA, Yeomans L, Montes F, Acuña H, Ayala A (1995) Influence of temperature on the slip velocity of semidilute xanthan gum solutions. Rheol Acta 34:474–482

    Article  Google Scholar 

  • Vieru D, Raul A (2011) Stokes flows of a Maxwell fluid with wall slip condition. Can J Phys 89:1061–1071

    Article  Google Scholar 

  • Yalcin H, Toker OS, Ozturk I, Dogan M, Kisi O (2012) Prediction of fatty acid composition of vegetable oils based on rheological measurements using nonlinear models. Eur J Lipid Sci Technol 114:1217–1224

    Article  Google Scholar 

  • Yaras P, Kalyon DM, Yilmazer U (1994) Flow instabilities in capillary flow of concentrated suspensions. Rheolog Acta 33:48–59

    Article  Google Scholar 

  • Yilmazer U, Kalyon DM (1989) Slip effects in capillary and parallel disk torsional flows of highly filled suspensions. J Rheol 33:1197–1212

    Article  Google Scholar 

  • Yoshimura A, Prud’homme R (1988) Wall slip corrections for Coutte and parallel disk viscometers. J Rheol 32:53–67

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to express the highest gratitude for financial support from FRGS Grant No. FP015-2014A awarded by Ministry of Higher Education (MOHE) Malaysia and RU Grant No. GPF064A-2018 awarded by Faculty of Engineering University of Malaya. The authors would like to thank Faculty of Engineering University of Malaya for the facilities provided for the experimental works.

Author information

Authors and Affiliations

  1. School of Hydraulic Engineering, Changsha University of Science and Technology, Changsha, 410114, China

    Ren Jie Chin & Sai Hin Lai

  2. Department of Civil Engineering, Faculty of Engineering, University of Malaya, 50603, Kuala Lumpur, Malaysia

    Ren Jie Chin, Sai Hin Lai, Wan Zurina Wan Jaafar & Ahmed Elshafie

  3. Institute of Ocean and Earth Sciences, University of Malaya, 50603, Kuala Lumpur, Malaysia

    Shaliza Ibrahim

Authors
  1. Ren Jie Chin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sai Hin Lai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shaliza Ibrahim
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Wan Zurina Wan Jaafar
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ahmed Elshafie
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sai Hin Lai.

Ethics declarations

Conflict of interest

No potential conflict of interest was reported by the authors.

Additional information

Communicated by V. Loia.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chin, R.J., Lai, S.H., Ibrahim, S. et al. ANFIS-based model for predicting actual shear rate associated with wall slip phenomenon. Soft Comput 24, 9639–9649 (2020). https://doi.org/10.1007/s00500-019-04475-5

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-019-04475-5

Keywords

Search

Navigation