Skip to main content
SpringerLink
Log in

Dynamic analysis for Governance–Pollution model with education promoting control

  • Focus
  • Published:
Soft Computing Aims and scope Submit manuscript

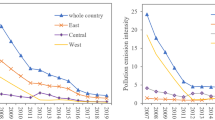
Abstract

The pollution and its governing problem have drawn the world’s extremely attention. To study the sensitivities of different governing methods, we formulate a dynamic system which is analyzed through two cases of noncooperation and with-cooperation among the enterprises and the government. The dynamic system describes the influences caused by the pollution control investment, the time delay of the abatement investment and the degree of the cooperation between the government and the enterprise. At last, we solve the optimal control problem based on turnpike theorem. It is shown that the economic output in a country could affect the steady state of the pollutant emissions. Moreover, the threshold value of time delay that the society can accept on the pollution control investment is non-integer. Furthermore, the environmental policies’ implementation could remedy the polluting weakness of the countries with higher economic outputs. Finally, we solve the optimal control problem in the G–P model through education promoting.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Aitziber I (2017) Optimal control of the Lotka–Volterra system: turnpike property and numerical simulations. J Biol Dyn 11(1):25–41

    Article  MathSciNet  Google Scholar 

  • Bao XD, Roossinck MJ (2013) A life history view of mutualistic viral symbioses: quantity or quality for cooperation. J Curr Opin Microbiol 16(4):514–518

    Article  Google Scholar 

  • Bulirsch R (1994) The maximum principle, Bellman’s equation, and Carathéodory’s work. J Optim Theory Appl 80(2):199–225

    Article  MathSciNet  MATH  Google Scholar 

  • Cai XQ, Li L, Wuc MQ, Yu LH (2016) Does environmental regulation drive away inbound foreign direct investment? Evidence from a quasi-natural experiment in China. J Dev Econ 123:73–85

    Article  Google Scholar 

  • Chiang SY (2012) An application of Lotka–Volterra model to Taiwan’s transition from 200 mm to 300 mm silicon wafers. J Technol Forecast Soc Change 79:383–392

    Article  Google Scholar 

  • Cobb CW, Douglas PH (1928) A theory of production. J Am Econ Rev 18(Supplement):139–165

    Google Scholar 

  • Dorfman R, Samuclson PA, Solow RM (1958) Linear programming and economic analysis. McGraw Hill, New York

    Google Scholar 

  • Gani A, Scrimgeour F (2014) Modeling governance and water pollution using the institutional ecological economic framework. J Econ Model 42:363–372

  • Horne Y, Strengers A Strempel (2016) Policing and polluting: the role of practices in contemporary urban environmental pollution governance. J Environ Sci Policy 66:112–118

    Article  Google Scholar 

  • Huang CS, Yu HX (2016) Study on the cooperation effect of energy enterprises under the participation of internet enterprises-based on Lotka–Volterra model. J Chin Int Energy 21:14–21

    Google Scholar 

  • Jie MH (2010) Empirical environmental investment efficiency of and policy recommendations. Chin J Popul Resour Environ 20(4):100–105

    Google Scholar 

  • Kanada MTF, Fujii M, Ohnishi S (2013) The long-term impacts of air pollution control policy: historical links between municipal actions and industrial energy efficiency in Kawasaki City, Japan. J Clean Prod 58:92–101

    Article  Google Scholar 

  • Lopez JMR, Sakhel A, Busch T (2017) Corporate investments and environmental regulation: The role of regulatory uncertainty, regulation-induced uncertainty, and investment history. J Eur Manag 35(1):91–101

    Article  Google Scholar 

  • Lotka AJ (1910) Contribution to the theory of periodic reaction. J Phys Chem C 14(3):271–274

    Article  Google Scholar 

  • Lotka AJ (1925) Elements of physical biology. Williams and Wilkins, Philadelphia

    MATH  Google Scholar 

  • Morris SA, Pratt D (2003) Analysis of the Lotka–Volterra competition equations as a technological substitution model. J Technol Forecast Soc Change 70:103–133

    Article  Google Scholar 

  • Neumann V (1937) A model of general economic equilibrium. Rev Econ Stud 13:1–9

    Article  Google Scholar 

  • Nonhebel G (1981) Industrial air pollution: British progress—a review. Atmos Environ 15(3):213–219

    Article  Google Scholar 

  • Peng Y, Zhou T, Xu YA (2013) Effects of environmental investment on emissions reduction of industrial waste gas under environmental regulation—GMM method based on Chinese provincial panel data. J Ind Technol Econ 8(8):123–131

    Google Scholar 

  • Searf AP (2015) Development economics. Renmin University of China Press, Beijing

    Google Scholar 

  • Söderberg C (2016) Complex governance structures and incoherent policies: implementing the EU water framework directive in Sweden. J Environ Manage 183(1):90–97

    Article  Google Scholar 

  • Song R, Xiao W, Wei Q (2013) Multi-objective optimal control for a class of nonlinear time-delay systems via adaptive dynamic programming. J Soft Comput 17(11):2109–2115

    Article  MATH  Google Scholar 

  • Sueyoshi T, Gotob M (2014) Investment strategy for sustainable society by development of regional economies and prevention of industrial pollutions in Japanese manufacturing sectors. J Energy Econ 42:299–312

    Article  Google Scholar 

  • Sussmann HJ, Willems JC (1997) 300 years of optimal control: from the brachystochrone to the maximum principle. IEEE Control Syst 17(3):32–44

    Article  Google Scholar 

  • Trélat E, Zuazua E (2015) The turnpike property in finite-dimensional nonlinear optimal control. J Differ Equ 258:81–114

    Article  MathSciNet  MATH  Google Scholar 

  • Volterra V (1926) Variazioni e fluttuazioni del numero d’individui in specie animali conviventi. Mem Acad Lincei Roma 2:31–113

    MATH  Google Scholar 

  • Wang D, Li SL (2014) DEA environmental assessment on U.S. Industrial sectors: investment for improvement in operational and environmental performance to attain corporate sustainability. J Energy Econ 45:254–267

    Article  Google Scholar 

  • Wang D, Liu D, Li H, Ma H, Li C (2016) A neural-network-based online optimal control approach for nonlinear robust decentralized stabilization. J Soft Comput 20(2):707–716

    Article  MATH  Google Scholar 

  • Xiong X, Zhang W, Li S, Wang F (2009) Analysis of stock index futures market competition based on Lotka–Volterra model. Chin J Syst Eng 24(5):581–588

    Google Scholar 

  • Yin XG (2015) Evaluation and empirical study on the efficiency of environmental investment. Mod Financ Econ J Tianjin 7:89–92

    Google Scholar 

  • Zhang SH, Worrell ZE, Wina CG (2015) Cutting air pollution by improving energy efficiency of China’s cement industry. J Energy Proc 83:10–20

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Statistics, Xi’an University of Finance and Economics, Xi’an, 710100, Shaanxi, People’s Republic of China

    Jiaorui Li & Siqi Yu

Authors
  1. Jiaorui Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Siqi Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jiaorui Li.

Ethics declarations

Conflicts of interest

Authors Jiaorui Li and Siqi Yu declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants performed by any of the authors.

Funding

This study was funded by National Natural Science Foundation of China under Grant Number [Grant Numbers: 11572231] and “Yan Ta” Scholars Project of Xi’an University of Finance and Economics.

Informed consent

Informed consent was obtained from all individual participants included in the study.

Additional information

Communicated by X. Li.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, J., Yu, S. Dynamic analysis for Governance–Pollution model with education promoting control. Soft Comput 22, 5311–5321 (2018). https://doi.org/10.1007/s00500-018-3019-y

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-018-3019-y

Keywords

Search

Navigation