Fast supervised novelty detection and its application in remote sensing

Abstract

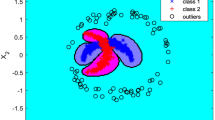
Multi-class supervised novelty detection (multi-class SND) is used for finding minor anomalies in many unknown samples when the normal samples follow a mixture of distributions. It needs to solve a quadratic programming (QP) whose size is larger than that in one-class support vector machine. In multi-class SND, one sample corresponds to $n_{c}$ variables in QP. Here, $n_{c}$ is the number of normal classes. Thus, it is time-consuming to solve multi-class SND directly. Fortunately, the solution of multi-class SND is only determined by minor samples which are with nonzero Lagrange multipliers. Due to the sparsity of the solution in multi-class SND, we learn multi-class SND on a small subset instead of the whole training set. The subset consists of the samples which would be with nonzero Lagrange multipliers. These samples are located near the boundary of the distributions and can be identified by the nearest neighbours’ distribution information. Our method is evaluated on two toy data sets and three hyperspectral remote sensing data sets. The experimental results demonstrate that the performance learning on the retained subset almost keeps the same as that on the whole training set. However, the training time reduces to less than one tenth of the whole training sets.