On network analysis using non-additive integrals: extending the game-theoretic network centrality

Abstract

There are large amounts of information that can be represented in terms of graphs. This includes social networks and internet. We can represent people and their interactions by means of graphs. Similarly, we can represent web pages (and sites) as well as links between pages by means of graphs. In order to study the properties of graphs, several indices have been defined. They include degree centrality, betweenness, and closeness. In this paper, we propose the use of Choquet and Sugeno integrals with respect to non-additive measures for network analysis. This is a natural extension of the use of game theory for network analysis. Recall that monotonic games in game theory are non-additive measures. We discuss the expected force, a centrality measure, in the light of non-additive integral network analysis. We also show that some results by Godo et al. can be used to compute network indices when the information associated with a graph is qualitative.

1 Introduction

Graphs are used to represent information that highlights the relationships between objects. They are the standard representation of social networks and internet. In the former case, we typically represent individuals as nodes and the relationship between individuals in terms of edges between the nodes. Similarly, when we represent (a subset of) internet as a graph, nodes correspond to web pages and edges correspond to links that relate web pages.

In order to study graphs, a few measures have been proposed. They are used to characterize and distinguish nodes (and edges) on the basis of the network structure. For example, there are measures used to determine which are the most influential nodes in a graph. As influential depends on the application and use, new indices are defined to cope with new aspects.

Centrality measures, betweenness, and closeness are some of these measures. In recent years, new measures have been defined. They are defined to quantify the “spreading power”. This is the case of the expected force, an index introduced in Lawyer (2015). Indices defined with a similar objective include the dynamic influence (Klemm et al. 2012) and the impact (Bauer and Lizier 2012). Other indices exist to evaluate particular properties related to nodes in the network as, e.g., trust (Wu et al. 2015, 2017).

Recent research on indices includes work on what is known as game-theoretic network centrality (Grofman and Owen 1982; Gómez et al. 2003; Michalak et al. 2013). Several papers and software systems have been written with the goal of using and developing the game-theoretic apparatus to evaluate the centrality of nodes in social networks. Game theory starts assuming the existence of a game on a reference set. A game is a set function on the reference set. In our setting, the reference set is the set of nodes and thus games are defined to evaluate sets of nodes. We can use for this purpose, e.g., group centrality (Everett and Borgatti 1999).

In game theory, we have indices (as, e.g., the Shapley value) that summarize the influence of a game. For example, the Shapley value for a node can be seen as an evaluation of the centrality of the node. While node centrality takes into account only the neighborhood of the node, the Shapley value would take into account the game for all subsets, that is, it will take into account the whole graph.

Although the idea is simple, there are difficulties on the actual computation of the indices because of the number of nodes and edges of some real graphs. Computationally efficient methods have been defined for this purpose. See, e.g., Michalak et al. (2013). Some of them are based on assuming that games have a particular structure (i.e., not any game is possible but they should be of a particular family).

In this work, we introduce another type of apparatus to the problem of network analysis. In short, we introduce the use of non-additive measures and integrals. This is a natural extension of the use of game theory.

First, note that the monotonic set functions currently used in the game-theoretic network centrality approach are examples of non-additive measures. Second, Choquet and Sugeno integrals permit to integrate information with respect to the non-additive measures. These integrals (also known as fuzzy integrals) generalize, e.g., the expected value. In this way, we can use the integrals to define indices in a compact way.

Then, we will introduce an index based on the expected force (Lawyer 2015). Our definition will be based on the Choquet integral. We will establish the relationship between our index and the expected force. We will discuss the use of other fuzzy integrals and the case that the information associated with a graph is not numerical but ordinal. We will link this research to some results by Godo and Torra (2000, 2001) and Godo and Zapico (2001, 2005).

The structure of the paper is as follows. In Sect. 2 we will review the main concepts on non-additive measures and Choquet and Sugeno integrals. In Sect. 3 we will review some concepts and indices for graph analysis. In Sect. 4 we will describe our approach for non-additive integral-based network analysis. The paper finishes with some conclusions.

2 Non-additive measures and integrals

Non-additive measures generalize additive measures, as, for example, probabilities. Formally, they are defined replacing the axiom of additivity by a monotonicity condition. That is, given two sets $A \subseteq B$ the only condition is that the measure of B is at least as great as the measure of A. We give their definition below following Torra and Narukawa (2007). See also Beliakov et al. (2008) and Grabisch et al. (2009).

Definition 1

Let X be a reference set. Then, a set function $\mu : \wp (X) \rightarrow [0,1]$ satisfying the two axioms below is a fuzzy measure (capacity or non-additive measure) $\mu$ on X.

• (i) $\mu (\emptyset ) = 0$, $\mu (X) = 1$ (boundary conditions)

• (ii) $A \subseteq B$ implies $\mu (A) \le \mu (B)$ (monotonicity)

Non-additive measures are also known as fuzzy measures, capacities, and monotonic games.

Given a function $f: X \rightarrow {{\mathbb {R}}}^+$, we can integrate the function f with respect to a non-additive measure by means of an integral. These integrals are known as fuzzy integrals. The Choquet and Sugeno integrals are two examples of these integrals. We give below the definition of the Choquet integral as it is the one that is applicable in our context.

A Choquet integral generalizes the Lebesgue integral. From the point of view of data aggregation, the most relevant property is that when the measure is additive, the Choquet integral of a function results in the weighted mean of the values of the function, i.e., the expected value when the measure is understood as a probability.

In other words, the Choquet integral can be seen as a generalization of the weighted mean where interactions between elements of X can be represented by means of the measure. The standard expectation corresponds to the case that there are no interactions between the elements of X.

The Choquet integral is defined as follows. The original definition was given in Choquet (1953/54). See, e.g., Torra and Narukawa (2007), Beliakov et al. (2008) and Grabisch et al. (2009) for properties of the Choquet integral.

Definition 2

Let X be a reference set, and let $\mu$ be a non-additive measure on X; then, the Choquet integral of a function $f: X \rightarrow {\mathbb {R}}^{+}$ with respect to the non-additive measure $\mu$ is defined by

$$\begin{aligned} (C)\int f {\hbox {d}} \mu = \sum _{i=1}^N [f(x_{s(i)}) - f(x_{s(i-1)})] \mu (A_{s(i)}), \end{aligned}$$

(1)

where $f(x_{s(i)})$ indicates that the indices have been permuted so that $0 \le f(x_{s(1)}) \le \dots \le f(x_{s(N)}) \le 1$, and where $f(x_{s(0)})=0$ and $A_{s(i)}=\{x_{s(i)}, \dots , x_{s(N)}\}$.

The Sugeno integral is an alternative fuzzy integral proposed by Sugeno (1974). Its definition follows.

Definition 3

Let $\mu$ be a non-additive measure on X; then, the Sugeno integral of a function $f: X \rightarrow [0,1]$ with respect to $\mu$ is defined by

$$\begin{aligned} (S)\int f {\hbox {d}} \mu = \max _{i=1,N} \min (f(x_{s(i)}), \mu (A_{s(i)})), \end{aligned}$$

(2)

where $f(x_{s(i)})$ indicates that the indices have been permuted so that $0 \le f(x_{s(1)}) \le ... \le f(x_{s(N)}) \le 1$ and $A_{s(i)}=\{x_{s(i)}, ..., x_{s(N)}\}$.

The Choquet integral integrates a function horizontally (as the Lebesgue integral) considering the measure of the support of each value. The Sugeno integral is all the larger as there exists an important set of criteria all of which are satisfied. Choquet and Sugeno integrals of the same function with respect to the same measure provide different and complementary summaries. The Choquet integral can be seen as a kind of mean, while the Sugeno integral is a kind of median. Recall that the number of citations and the h-index of an author are just Choquet and Sugeno integrals of the same function with respect to the same measure (see Torra and Narukawa 2008 for details). This type of complementarity can be of interest in network analysis. Observe that in a scale-free network, the mean and the median degree can be quite different.

3 Graph analysis: centrality measures

Given a set of nodes V, a graph G is defined as the pair $G=(V,E)$ where $E \subseteq V \times V$. When edges have no orientation and the edge $(n_1, n_2)$ is identical to the edge $(n_2, n_1)$, we say that the graph is undirected. Otherwise, a graph is said to be directed. Unless stated otherwise, we consider directed graphs in this paper.

There are several centrality measures in the literature to evaluate the influence or importance of nodes. Degree centrality, closeness, and betweenness are the most well-known ones. Recently, Lawyer (2015) introduced the expected force. The relevance of a node is measured in terms of its capability of infecting other nodes. Its definition is to take into account how infections are spread in a network. A formal definition follows. We begin with the concept of infection path.

Definition 4

Let $G=(V,E)$ be a graph. For any node $n \in V$, we define an infection path from n recursively on its length.

• The infection path of length 0 for node n is just the node n. We denote this by $p_0 = \{(0,n,n)\}$.

• $p_{s+1}$ is an infection path of length $s+1$ for node n if there is an infected path of length s from node n denoted by $p_s$, and if $p_{s+1}$ is $p_{s}$ union the tuple $(s+1,n_0,n_1)$ where $n_0$ is a node in $p_{s}$ (i.e., $n_0 \in V(p_s)$), $n_1$ is not a node in $p_{s}$ (i.e., $n_1 \notin V(p_s)$), $(n_0,n_1)$ is an edge of the graph (i.e., $(n_0,n_1) \in E$), and $(n_0,n_1)$ is not already in $p_s$ (i.e., $(n_0,n_1) \notin E(p_s)$). We denote this by $p_{s+1}=p_s \cup \{(s+1,n_0,n_1)\}$.

Observe that we use V(p) and E(p) to denote, respectively, the nodes and edges of the infection path p. Naturally, $V(p)=\cup _{(r,n,n') \in p} \{n, n'\}$, and $E(p)=\cup _{(r,n,n') \in p, n \ne n'} \{(n,n')\}$.

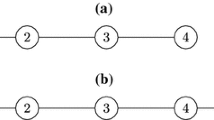
The definition of infection paths includes an index for each edge as the order in which the edges are added is relevant. We give an example below with Fig. 1 and 2 that shows paths whose only difference is the order in which edges are added to the path.

The expected force for a node i is based on considering all possible infection paths p for a given number of steps s. The measure also considers the connection degree of the path. This connection degree is defined in terms of the neighbors of the nodes in the path as follows.

Definition 5

Let $G=(V,E)$ be a graph, and let Ne(n) denote the neighbors of node $n \in V$. Then, the connection degree of a set A is defined as follows:

$$\begin{aligned} od(A) = \left| \cup _{n \in A} Ne(n) {{\setminus }} A \right| . \end{aligned}$$

The connection degree of a path p is defined as follows

$$\begin{aligned} od(p) = od(V(p)), \end{aligned}$$

where V(p) are the nodes in the path p.

Using the previous definitions, we can introduce now the expected force.

Definition 6

(Lawyer 2015) Let $G=(V,E)$ be a graph, let $J_s(i)$ represent all infection paths from the ith node that infect s nodes, and let od(p) denote the connection degree of path p. Then, the expected force of node i is defined by

$$\begin{aligned} ExF(i)=-\sum _{p \in J_s(i)} {\bar{d}}(p) \log {\bar{d}}(p). \end{aligned}$$

where

$$\begin{aligned} {\bar{d}}(p)=\frac{od(p)}{\sum _{p' \in J_s(i)} od(p')}. \end{aligned}$$

Note that using ${\bar{d}}(p)$ instead of od(p) is to ensure that we are dealing with a probability distribution and, thus, that the entropy is an appropriate measure. Lawyer (2015) uses Shannon entropy in the definition, but other types of entropy may also be used.

Fig. 1

Graph with 4 nodes to illustrate the computation of $J_s(i)$

Fig. 2

Infection paths for the graph with 4 nodes in Fig. 1. This corresponds to $J_2(i)$ for the node in Fig. 1

To illustrate the computation of the infection paths and the expected force, we give a small graph of only 4 nodes and 4 edges in Fig. 2. We assume that the graph is undirected. Note that the infection paths depend on the node considered. We have marked in the figure the node i that is considered for computing the paths.

Then, in Fig. 2 we illustrate the infection paths for the node i when the number of infections is 2 [as used in Lawyer (2015)]. As we have two infections, we have always two nodes in addition to the node i.

The computation of the infection paths for two infections (i.e., $s=2$) needs to consider all nodes at distance 1 and all nodes at distance 2. Then, for each pair of nodes $n_1$ and $n_1'$ at distance 1, we have two infection paths if there is no edge between $n_1$ and $n_1'$, and four infection paths when there is an edge between them. This is illustrated in Fig. 2. The figure shows all the infection paths defined for nodes at distance one from i according to the graph in Fig. 1. The numbers in each figure represent the order in which infection took place. In addition, for each node $n_2$ at distance 2 we have one infection path. There is no node at a minimum distance of 2 in the graph of Fig. 1.

Then, note that for each of the eight paths in Fig. 2 its connection degree is 1 (because there is only one node left in the graph and it is accessible from any infection path). Because of that, $od(p)=1/8$ for all p and $ExF(i)=-\sum _p (1/8) \log (1/8) = 3$.

4 Network analysis using non-additive integrals

Given a graph $G=(V,E)$, we can consider measurable properties on the nodes and on the edges. However, we may also consider properties on sets of nodes and on sets of vertices. In particular, we can consider non-additive properties.

In this paper, we focus on the set of nodes, as we evaluate the importance of nodes. Because of that, we consider set functions that apply to any subset of the original nodes. So, let $A \subseteq V$, then $\mu (A)$ will measure some characteristic of the set A. Naturally, $\mu$ will depend on the context. Our only constraint is that $\mu$ is monotonic with respect to set inclusion. We discuss two examples in the next section to illustrate the relevance of the concept.

4.1 Non-additive measures on sets of nodes

Our first example is based on betweenness centrality. It is known that betweenness evaluates the centrality of a node with respect to the number of shortest paths in the graph that go through a node. We can extend this concept to any set of nodes A. Let us define $\mu (A)$ as the number of shortest paths that go through any of the nodes in A. Naturally, this measure is monotonic, the more nodes we have in A, the more shortest paths that go through A; and satisfies $\mu (\emptyset )=0$. We can normalize this measure to have $\mu (V)=1$ dividing it by the total number of shortest paths.

Our second example is based on the connection degree (i.e., Definition 5). Note that when several nodes in A are connected to the same node n, this node n only contributes in 1 to od. Because of this, od(A) is not additive. In general, for any disjoint sets A and B, $od(A \cup B) \le od(A) + od(B)$. This is illustrated in Fig. 3. Two disjoint sets A and B are defined. A is connected to nodes $\{c,g,d\}$, and B is connected to nodes $\{d,g,h,e\}$. Therefore, $od(A)=3$ and $od(B)=4$. Moreover, $A \cup B$ is connected to nodes $\{c,g,d,h,e\}$ therefore $od(A \cup B)=5$.

Fig. 3

A graph and two subsets of nodes A and B from the set of vertices

However, the function od does not satisfy the monotonicity condition. For example, if $A=V {\setminus } \{n\}$ for a connected graph with at least two nodes n and $n_1$, $od(A)=1$ while $od(V=A \cup \{n\})=0$.

In order to have a monotonic measure, we consider $d(A)=|A|+od(A)$. The measure is still non-additive as the following example shows.

$$\begin{aligned}d(A \cup B) = 6 + 5 \ne d(A) + d(B) = 3 + 3 + 3 + 4.\end{aligned}$$

As we expect the measure to be normalized, we divide the expression by the number of nodes. Accordingly, we have for $A \subseteq V$ the following:

$$\begin{aligned} \mu (A)=\frac{d(A)}{|V|}=\frac{|A|+od(A)}{|V|} \end{aligned}$$

(3)

Recall that the monotonic measure $|A|+od(A)$ was used in Suri and Narahari (2008). Here we normalize it to be in [0, 1].

These measures are based on properties of the nodes: their degree. A different approach in the same line is when we have a possibility distribution on the nodes, and this distribution is used to build the measure for any set of nodes. We can use in this context results from Godo and Zapico (2001, 2005). Similarly, we can also consider defining monotonic measures based on the density of sets (i.e., $|E_A|/(|A|(|A|-1))$ where $E_A$ are the edges $(n,n')\in E$ where both n, $n' \in A$). In Narukawa and Torra (2005) and Torra and Narukawa (2012), we proposed the definition of measures based on values assigned to edges (i.e., a function $\nu : E \rightarrow [0,1]$). Then, given a pseudo-addition $\oplus$ (i.e., a commutative, monotonic, associative, continuous, and with $0 \oplus a = a \oplus = a$ operator) a measure for any set of nodes is defined by

$$\begin{aligned} \mu (A):=\frac{\sup \{\oplus _{(x,y)\in I} \nu ((x,y)) | I \subset A, I \in {{{\mathcal {T}}}}_E \}}{\mu (N)} \end{aligned}$$

(4)

where ${{\mathcal {T}}}_E$ is the set of all fuzzy trees of the graph (i.e., a subgraph that does not contain a cycle). Then, we define $\mu '(A):=\mu (A)/\mu (V)$ to have a normalized measure.

Following Suri and Narahari (2008) and Michalak et al. (2013), we may consider indices for set functions. For example, we can consider the Shapley and the Banzhaf power indices for $\mu$. This will assign an importance to each node in the graph taking into account the set function. This can be understood as a measure of how a node contributes to the overall connectivity of other nodes. These indices could be applied to the two measures in this section.

4.2 Non-additive integrals network analysis

We go now one step further extending the game-theoretic approach by means of non-additive measures and integrals. The main idea is that in addition to the measure on the set of nodes V, we have a function (or functions) that evaluates each node V.

Then, if we have the non-additive measure on the set of nodes V, and a function f, we can compute the Choquet integral of f with respect to the measure. This defines an overall measure (an aggregation of f).

To be more explicit, if the function is global, we compute a global measure. On the contrary, if we have a collection of measures $\{f_v\}_{v \in V}: V \rightarrow {{\mathbb {R}}}^+$ (i.e., a function $f_V$ for each node $v \in V$), then, we will have an index for each node to be used for node analysis. This is formalized in the next definitions.

Definition 7

Let $G=(V,E)$ be a graph. Let $\mu$ be a non-additive measure on V. Let f be a function on V into ${{\mathbb {R}}}^+$. Then, we define a global index of the graph as follows $GI(v) = (C)\int f {\hbox {d}} \mu .$

Definition 8

Let $G=(V,E)$ be a graph. Let $\mu$ be a non-additive measure on V. Let $\{f_v\}_{v \in V}$ be a collection of functions on V into ${{\mathbb {R}}}^+$. Then, we can define an index for nodes $v \in V$ as follows:

$$\begin{aligned} I(v) = (C)\int f_v {\hbox {d}} \mu . \end{aligned}$$

It is important to stress that in Definition 8, we consider a function $f_v$ for each node $v \in V$, and that each function $f_v$ is of the form $f_v: V \rightarrow {{\mathbb {R}}}^+$. Compare this with Definition 7 where we have a global index as there is a single function f for the whole graph (e.g., importance of the graph, population of a town if the graph represents a map).

Let us illustrate this with an example. The example evaluates the importance of a node on the basis of its connections (out-degree).

Example 1

Let $G=(V,E)$ be a graph. Let $\mu$ be the measure described in Eq. (3). Let the set of functions $f_v$ for $v \in V$ be defined as follows: $f_{v}(n)=1$ if n is a neighbor of v, and $f_{v}(n)=0$ otherwise. Then, we define the relevance of a node by

$$\begin{aligned} R(v)=(C)\int f_v \mu . \end{aligned}$$

Using the properties of the Choquet integral, we have that for any node n, if Ne(n) is the set of neighbors of n, then R(v) corresponds to

$$\begin{aligned} R(v)= & {} \mu (Ne(v))=\frac{d(Ne(v))}{|V|}\\= & {} \frac{|Ne(v)|+od(Ne(v))}{|V|}=\frac{|\{u|l(u,v)\le 2\}|}{|V|}. \end{aligned}$$

where l(u, v) is the length of the shortest path between nodes u and v.

Example 2

Let G and $\mu$ as in Example 1. Let the set of functions $f_v$ for $v \in V$ be defined as $f_v(n)=1$ if and only if the shortest path between v and u is less than or equal than 2. Then,

$$\begin{aligned} R(v)=\mu (\{u|l(u,v)\le 2\})=\frac{|\{u|l(u,v)\le 3\}|}{|V|}. \end{aligned}$$

Let us illustrate the definition above with another example. Example 1 uses functions $f_v$ defined as 1 for the neighbors of the node v and zero; otherwise, Example 2 uses functions $f_v$ defined as 1 if the shortest path to v is less than 2. In the next example, we have that the value of the function $f_v(n)$ decays with the distance (shortest path from a node n to v).

Example 3

Let $G=(V,E)$ be a graph. Let $\mu$ be the measure described in Eq. (3). Let l(v, n) be the length of the shortest path from v to n. Then, for any node $v\in V$ we define $f_{v}(n)=1/2^{l(v,n)}$. Using these expressions, we define the rumor spreading capability (RI for rumor increbrescit) of a node by

$$\begin{aligned} {\hbox {RI}}(v)=(C)\int f_v \mu . \end{aligned}$$

Let us consider the computation of this measure for a few graphs of 11 nodes. If the graph is unconnected, then ${\hbox {RI}}=1/11$ for any node. If the graph is regular with all nodes of degree 2, then ${\hbox {RI}}=0.4431818$ for any node. There is no graph with degree 3 with 11 nodes. If we leave one node with degree 2 (see Fig. 4), then it is graphical but different nodes will have different degrees. In particular, node 1 has ${\hbox {RI}}=0.65909094$ and node 5 has ${\hbox {RI}}=0.54545456$. If the graph is complete, then ${\hbox {RI}}=1.0$.

Fig. 4

Graph with 10 nodes with degree 3 and one with degree 2

4.3 Properties

The properties of non-additive measures and integrals permit to infer some properties on the index.

Proposition 1

The following holds:

• If $m_v=\max _{v'} f_v(v')$, then $0 \le I(v) = (C)\int f_v {\hbox {d}} \mu \le m_v$.

• Let $G=(V,E)$ be a subgraph of $G'=(V',E')$ if $V=V'$ and $E \subseteq E'$. Then, if $\mu _G(A) \le \mu _{G'}(A)$ for all A, $I_G(v) \le I_{G'}(v)$ for all $v \in V$.

The first property gives bounds to the indices.

The second property states that the index is monotonic with respect to graph inclusion (if the measure also behaves in a monotonic way). Note that the monotonicity condition on the measure means that the measure should account for the fact that $G'$ is more connected than G. If this is the case, the index increases. That is, if the more connected is the graph, the larger the measure, then, the larger the index.

4.4 Revisiting and revising the expected force

In this section, we revisit the expression for the expected force (Definition 6). We first rewrite the expression taking into account the fact that within $J_s(i)$ we find several infection paths with the same set of nodes. That is, we may have two different paths with the same set of nodes (i.e., $p_1 \ne p_2$ but $V(p_1)=V(p_2)$). Assume that there are k different sets of nodes. Then, ${\mathcal {C}}_s(i)=\{$$C_1$, $\dots$, $C_k\}$ denotes the collection of sets of nodes in $J_s(i)$ that are unique.

Let ${\hbox {oc}}_i(C)$ be the number of occurrences of a set C in $J_s(i)$. That is, ${\hbox {oc}}_i(C)=|\{p \in J_s(i) | V(p)=C\}|$. For example, in Fig. 2 we have three different sets of nodes (i.e., each row in Fig. 2) so ${\mathcal {C}}_2(i)=\{C_1, C_2, C_3\}$, and ${\hbox {oc}}_i(C_1)$, ${\hbox {oc}}_i(C_2)$, and ${\hbox {oc}}_i(C_3)$ are, respectively, 4, 2, and 2.

Let us rewrite the expression of expected force in Definition 6 using unique sets of infected nodes. We use for this purpose ${\tilde{d}}(C) = d(C) / \sum _{C' \in {\mathcal {C}}_s(i)} {\hbox {oc}}_i(C')$.

$$\begin{aligned} ExF(i)= & {} -\sum _{p \in J_s(i)} {\bar{d}}(p) \log {\bar{d}}(p) \\= & {} -\sum _{C \in {\mathcal {C}}_s(i)} {\hbox {oc}}_i(C) {\tilde{d}}(C) \log {\tilde{d}}(C) \end{aligned}$$

Let $f_i(n)$ be the function that corresponds to the number of infections of node n from i in s steps using any of the possible paths in $J_s(i)$. That is,

$$\begin{aligned} f_i(n)=|\{p \in J_s(i)\text {~and~}n \in p\}|=\sum _{C \in {\mathcal {C}}_s(i), n \in C} {\hbox {oc}}_i(C). \end{aligned}$$

(5)

Note that $f_i(n)=0$ implies ${\hbox {oc}}_i(C)=0$. Let us define $w_n(C)={\hbox {oc}}_i(C)/f_i(n)$ when $n \in C$ and $f_i(n) \ne 0$, and $w_n(C)=0$ otherwise. Then, we can rewrite the expected force to make explicit the role of nodes as follows.

$$\begin{aligned} ExF(i)= & {} \sum _{n \in V} f_i(n) \sum _{n \in C \in {\mathcal {C}}_s(i)} w_n(C) \left( - {\tilde{d}}(C) \log {\tilde{d}}(C)\right) \nonumber \\ \end{aligned}$$

(6)

This expression shows that the contribution of a node is larger when there are more infection paths in which the node appears and that the contribution for each path is weighted by the proportion of times; this path is the cause of the infection (i.e., $w_n(C)$). In fact, the inner summatory can be seen as a weighted mean (WM) with weights $w=(w_n(C_1), \dots , w_n(C_k))$:

$$\begin{aligned} {\hbox {WM}}_{w}(- {\tilde{d}}(C_1) \log {\tilde{d}}(C_1), \dots , - {\tilde{d}}(C_k) \log {\tilde{d}}(C_k)), \end{aligned}$$

The number of infections is very relevant in this measure. So, a very connected graph will have maximum measure for all nodes as $-{\tilde{d}}(C) \log {\tilde{d}}(C)$ will be maximum, and $f_i(n)$ also maximum. Instead, a connected graph with degree 2 has low measure for all nodes as both $-{\tilde{d}}(C) \log {\tilde{d}}(C)$ and $f_i(n)$ will be lower.

In the light of this observation, we define another measure of force for a given node based on Definition 8. We call it out-degree expected force.

Definition 9

Let $G=(V,E)$ be a graph. Let $\mu$ be the measure in Eq. (3). Let s be a number of steps. Let $f_{i}(n)$ be the family of functions defined in Eq. (5). Then, the out-degree expected force of node i is defined by

$$\begin{aligned} {\hbox {ODEF}}(i) = CI_{\mu }(f_i). \end{aligned}$$

Lawyer (2015) discusses the use of entropy in the definition of the expected force as a way to overcome the fact that “complex networks have scale-free degree distributions” and that “the moments of scale-free distributions are divergent”. Comparing ExF(i) with the alternative but similar in rationale, we obtain the definition

$$\begin{aligned} ExF_\mathrm{AM}(i)=\frac{1}{|J_s(i)|} \sum _{p \in J_s(i)} {\bar{d}}(p) \end{aligned}$$

where $ExF_\mathrm{AM}$ is just an arithmetic mean (AM) of the connection degrees.

Our definition somehow swaps the role of the distribution. Note that there are two elements that are taken into account. One is the connection degree. In a way similar to Lawyer (2015), the connection degree is taken for sets of nodes and not for individual nodes. Because of that, it is natural to use it to define a non-additive measure (which is a set function). A second element we may consider from ExF is the number of infections of a node using any possible path. This is naturally a function of a node. In this way, the Choquet integral integrates this latter function with respect to the measure. This is the rationale behind Definition 9.

Note also that the non-additive measure is fixed for any graph and independent on the node we are considering when computing its force. On the contrary, the function depends on the node.

Using results from Choquet integrals, we can prove the following.

Proposition 2

For any graph G and any node i, given a number of steps s, $ODEF(i) \in [0,(|V|-1)^{s(s+1)/2}]$.

Proof

The upper bound of this proposition takes into account that we can consider any possible path for infection, and that the out-degree of a node is at most $|V|-1$. This upper bound cannot be reached because not all infection paths are valid (e.g., infecting a node twice is not allowed). In general, when the number of edges of nodes is much less than $|V|-1$, ${\hbox {ODEF}}(i)$ can be much lower than this upper bound. $\square$

The proposition shows that the range of the measure depends on the number of possible paths. This depends on s and the topology of the graph.

Proposition 3

Let $G_0$ denote an unconnected graph, let $G_2$ be a connected graph where all nodes have degree two, let $G_x$ be a complete graph. Then,

$$\begin{aligned} ODEF_{G_0}(i) \le ODEF_{G_2}(i) \le ODEF_{G_x}(i) \end{aligned}$$

for any node i.

Proof

The definition implies that

• $\mu _0(A)=|A|/|V|$,

• $\frac{|A|}{|V|} \le \mu _2(A)\le (1/|V|) \cdot \min (3|A|, |V|)$ and

• $\mu _x(A)=|V|/|V|=1$

for all A. Then,

$$\begin{aligned} CI_{\mu _{0}}(f) \le CI_{\mu _{2}}(f) \le CI_{\mu _{x}}(f) \end{aligned}$$

for any f.

Then, if G is a subgraph of $G'$, then $f_{G} \le f_{G'}$. This is so because the number of infections will be smaller (less ways to reach a node). This is so for any s.

Therefore, $f_0 \le f_2 \le f_x$.

From this it follows

$$\begin{aligned} CI_{\mu _{0}}(f_0) \le CI_{\mu _{2}}(f_1) \le CI_{\mu _{x}}(f_x) \end{aligned}$$

and the proof is complete. $\square$

In fact, as when G is a subset of $G'$, it follows that $\mu _G(A) \le \mu _G'(A)$ for all A, and as we have discussed in the proof $f_G \le f_{G'}$, the following more general result follows.

Proposition 4

Let G a subgraph of $G'$ then $ODEF_G(i) \le ODEF_{G'}(i)$ for any node i in G.

These last results are related to the second property in Proposition 1. Nevertheless, the function on the nodes in Proposition 1 is kept constant when replacing G by $G'$. This is not the case here because in the out-degree expected force the function depends on the graph itself.

All definitions above can be rewritten with a Sugeno integral. Then, we can easily prove an analogous proposition to Proposition 3 but using a Sugeno integral. As explained above, Choquet and Sugeno integral can provide different and complementary summaries.

While the Choquet integral is to be applied to numerical data, Sugeno integral can be applied to data in ordinal scales (i.e., when both measures and functions result in values in ordinal scales). For ordinal scales, it is also relevant to the work by Godo and Torra (2000, 2001). They introduced aggregation operators for ordinal scales that were based on t-norms and t-conorms and that are ordinal counterparts of the weighted mean and the Choquet integral. The rationale behind these definitions is to encompass a “more genuine notion of average”. Note that the output of the median and the Sugeno integral is one of the values being integrated or taken into consideration in the measure. This is not the case in the weighted mean and the Choquet integral. That is, mean of 1 and 5 is 3 even 3 is not a value to be aggregated. Godo and Torra (2001) proposed a qualitative Choquet integral where some average is allowed (not for consecutive values as the output is in the original ordinal scale).

In relation to the application of this approach, it is important to observe that while we need $2^{|V|}$ values to properly define a measure, computing the fuzzy integral only once requires only the |V| values of the measure actually used in the computation. Naturally, multiple applications of the integral may require us to know the whole measure.

5 Conclusion

In this paper, we have introduced the use of non-additive measures and integrals for network analysis. We have introduced a definition for the Choquet expected force based on the Choquet integral and a non-additive measure that corresponds to the connection degree of a set.

We have shown that this approach can also be applied to networks that solely contain categorical information (in ordinal scales). Results by Lluís Godo can be used in this area to compute categorical indices of network centrality.

Future lines of research include the development of efficient algorithms as well as approximate solutions for large-scale graphs, and their use to evaluate and compare graphs. In particular, we are interested in comparing a given graph with its masked and synthetic version (Torra 2017) to evaluate the utility of the latter and to assess the performance of protection mechanisms for data privacy.