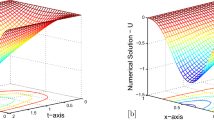
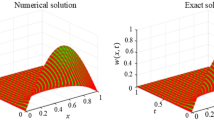
Abstract
Many numerical methods applied on a Shishkin mesh are very popular in solving the singularly perturbed problems. However, few approaches are used to obtain the Shishkin mesh transition parameter. Thus, in this paper, we first use the cubic B-spline collocation method on a Shishkin mesh to solve the singularly perturbed convection–diffusion problem with two small parameters. Then, we transform the Shishkin mesh transition parameter selection problem into a nonlinear unconstrained optimization problem which is solved by using the self-adapting differential evolution (jDE) algorithm. To verify the performance of our presented method, a numerical example is employed. It is shown from the experiment results that our approach is efficient. Compared with other evolutionary algorithms, the jDE algorithm performs better and with more stability.



Similar content being viewed by others
References
Abbass HA (2002) The self-adaptive Pareto differential evolution algorithm. In: Proceedings of the congress evolutionary computation, Honolulu, HI, pp 831–836
Abderazek H, Ferhat D, Atanasovska I (2015) A differential evolution algorithm for tooth profile optimization with respect to balancing specific sliding coefficients of involute cylindrical spur and helical gears. Adv Mech Eng 7(9):1–11
Ali MM, Törn A (2004) Population set-based global optimization algorithms: some modifications and numerical studies. Comput Oper Res 31(10):1703–1725
Ali M, Ahn CW, Pant M (2014) Multi-level image thresholding by synergetic differential evolution. App Soft Comput 17:1–11
Ali MZ, Awad NH, Suganthan PN, Duwairi RM, Reynolds RG (2016a) A novel hybrid Cultural Algorithms framework with trajectory-based search for global numerical optimization. Inf Sci 334–335(C):219–249
Ali MZ, Suganthan PN, Reynolds RG, Al-Badarneh AF (2016b) Leveraged neighborhood restructuring in cultural algorithms for solving real-world numerical optimization problems. IEEE Trans Evol Comput 20(2):218–231
Bigge J, Bohl E (1985) Deformations of the bifurcation diagram due to discretization. Math Comput 45(172):393–403
Brest J, Greiner S, Boskovic B et al (2006) Self-adapting control parameters in differential evolution: a comparative study on numerical benchmark problems. IEEE Trans Evolut Comput 10(6):646–657
Das S, Konar A (2009) Automatic imageg pixel clustering with an improved differential evolution. Appl Soft Comput 9(1):226–236
Gämperle R, Müller SD, Koumoutsakos P (2002) A parameter study for differential evolution. In: Grmela A, Mastorakis NE (eds) Advances in intelligent systems, fuzzy systems, evolutionary computation. WSEAS Press, Interlaken, pp 293–298
Gong W, Cai Z (1976) Parameter optimization of PEMFC model with improved multi-strategy adaptive differential evolution. Eng Appl Artif Intel 27(C):28–40
Gong W, Cai Z, Ling CX (2011) DE/BBO: a hybrid differential evolution with biogeography-based optimization for global numerical optimization. Soft Comput 15(4):645–665
Gong W, Zhou A, Cai Z (2015) A multioperator search strategy based on cheap surrogate models for evolutionary optimization. IEEE Trans Evolut Comput 19(5):746–758
Gracica JL, O’Riordan E, Pickett ML (2006) A parameter robust second order numerical method for a singularly perturbed two-parameter problem. Appl Numer Math 56(7):962–980
Hansen N, Muller SD, Koumoutsakos P (2003) Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol Comput 11(1):1–18
Herceg D (2011) Fourth-order finite-difference method for boundary value problems with two small parameters. Appl Math Comput 218(2):616–627
Kadalbajoo MK, Yadaw AS (2008) B-spline collocation mehod for a two-parameter singularly pertubed convection-diffusion boundary value problems. Appl Math Comput 201(1–2):504–513
Kennedy J, Eberhart RC (1995) Particle swarm optimization. In: Proceeding of the IEEE international conference on neural networks (Perth, Australia). IEEE Service Ceter, Piscataway, NJ, pp 1942–1948
Liang JJ, Qin AK, Suganthan PN, Baskar S (2006) Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans Evolut Comput 10(3):281–295
Linß T (2010) A posteriori error estimation for a singularly perturbed problem with two small parameters. Int J Numer Anal Model 7(3):491–506
Linß T, Roos HG (2004) Analysis of a finite-difference scheme for a singularly perturbed problem with two small parameters. J Math Anal Appl 289(2):355–366
Liu W, Wang P, Qiao H (2012) Part-based adaptive detection of workpieces using differential evolution. Signal Process 92(2):301–307
Liu J, Lampinen J (2005) A fuzzy adaptive differential evolution algorithm. Soft Comput 9(6):448–462
Lynn N, Suganthan PN (2015) Heterogeneous comprehensive learning particle swarm optimization with enhanced exploration and exploitation. Swarm Evol Comput 24:11–24
Matthews S, O’Riordan E, Shishkin GI (2002) A numerical method for a system of singularly perturbed reaction–diffusion equations. J Comput Appl Math 145:151–166
Miller JJH, O’Riordan E, Shishkin GI (1996) Fitted numerical methods for singular perturbation problems. Error estimates in the maximum norm for linear problems in one and two dimensions. World Scientific, Singapore
O’Malley RE Jr (1967) Two-parameter singular perturbation problems for second order equations. J Math Mech 16:1143–1164
Omran MGH, Salman A, Engelbrecht AP (2005) Self-adaptive differential evolution. In: Lecture notes in artificial intelligence. Springer, Berlin, pp 192–199
Ono I, Kobayashi S (1997) A real coded genetic algorithm for function optimization using unimodal normal distributed crossover. In: International conference on genetic algorithms, East Lansing, MI, USA, pp 246–253
Ouyang A, Yang Z (2016) An efficient hybrid algorithm based on harmony search and invasive weed optimization. In: 2016 12th international conference on natural computation, fuzzy systems and knowledge discovery (ICNC-FSKD), Changsha, pp 167–172. doi:10.1109/FSKD.2016.7603169
Ouyang A, Li K, Truong TK, Sallam A, Sha EHM (2014) Hybrid particle swarm optimization for parameter estimation of Muskingum model. Neural Comput Appl 25(7–8):1785–1799
Ouyang A, Tang Z, Zhou X, Xu Y, Pan G, Li K (2015) Parallel hybrid PSO with CUDA for lD heat conduction equation. Comput Fluids 110:198–210
Ouyang A, Peng X, Liu Y, Fan L, Li K (2016a) An efficient hybrid algorithm based on HS and SFLA. Int J Pattern Recognit Artif Intell 30(5):1659012 (1–25)
Ouyang A, Peng X, Wang Q, Wang Y, Truong TK (2016b) A parallel improved iwo algorithm on gpu for solving large scale global optimization problems. J Intell Fuzzy Syst 31(2):1041–1051
Piotrowski AP (2014) Diiferential Evolution algorithms applied to neural network training suffer from stagnation. Appl Soft Comput 21:382–406
Qin AK, Suganthan PN (2005) Self-adaptive differential evolution algorithm for numerical optimization. In: Proceedings of the IEEE congress evolutionary computation, Edinburgh, Scotland, pp 1785–1791
Qin AK, Huang VL, Suganthan PN (2009) Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans Evolut Comput 13(2):398–417
Qu BY, Suganthan PN, Das S (2013) A distance-based locally informed particle swarm model for multimodal optimization. IEEE Trans Evol Comput 17(3):387–402
Rahnamayan S, Tizhoosh HR, Salama MMA (2008) Oppositionbased differential evolution. IEEE Trans Evolut Comput 12(1):64–79
Rönkkönen J, Kukkonen S, Price KV (2005) Real-parameter optimization with differential evolution. In: Proceedings of the IEEE congress evolutionary computation, Edinburgh, Scotland, pp 506–513
Roos HG, Uzelac Z (2003) The SDFEM for a convection–diffusion problem with two small parameters. Comput Methods Appl Math 3(3):443–458
Srorn R, Price K (1997) Differential evolution: a simple and efficient adaptive scheme for global optimization over continuous spaces. J Global Optim 11(4):341–359
Suganthan PN (1999) Particle swarm optimiser with neighbourhood operator. In: Proceedings of the 1999 congress on evolutionary computation, 1999 (CEC 99), Washington, DC
Wu G, Mallipeddi R, Suganthan PN, Wang R, Chen H (2016) Differential evolution with multi-population based ensemble of mutation strategies. Inf Sci 329:329–345
Xu Y, Li K, Hu J, Li K (2014) A genetic algorithm for task scheduling on heterogeneous computing systems using multiple priority queues. Inf Sci 270:255–287
Xu Y, Li K, He L, Zhang L (2015) A hybrid chemical reaction optimization scheme for task scheduling on heterogeneous computing systems. IEEE Trans Parallel Distrib Syst 26(12):3208–3222
Zaharie D (2003) Control of population diversity and adaptation in differential evolution algorithms. In: Matousek R, Osmera P (eds) Proceeding of the mendel 9th international conference soft computing, Brno, Czech Republic, pp 41–46
Zaharie D, Petcu D (2003) Adaptive pareto differential evolution and its parallelization. In: Proceedings of the 5th international conference on parallel process applied mathematics, Czestochowa, Poland, pp 261–268
Zhang J, Sanderson AC (2009) Jade: adaptive differential evolution with optional external archive. IEEE Trans Evolut Comput 13(5):945–958
Acknowledgements
This work was supported by the National Natural Science Foundation of China (11301044, 11401054, 61662090, 11461011), the general Project of Hunan provincial education department (14C0047), the Natural Science Foundation of Guizhou Provincial Education Department (No. KY[2016]018), the Scientific Research Fund of Hunan Provincial Education Department (No. 13C333), the Doctoral Foundation of Zunyi Normal College (No. BS[2015]13), the open fund of Key Laboratory of Guangxi High Schools for Complex System and Computational Intelligence (No. 15CI03D), Natural Science Foundation of Guangxi Education Department (No. ZD2014080).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Luo, XQ., Liu, LB., Ouyang, A. et al. B-spline collocation and self-adapting differential evolution (jDE) algorithm for a singularly perturbed convection–diffusion problem. Soft Comput 22, 2683–2693 (2018). https://doi.org/10.1007/s00500-017-2523-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-017-2523-9