Abstract
In this paper, inspired by the previous work of Franco Montagna on infinitary axiomatizations for standard \(\mathsf {BL}\)-algebras, we focus on a uniform approach to the following problem: given a left-continuous t-norm \(*\), find an axiomatic system (possibly with infinitary rules) which is strongly complete with respect to the standard algebra  This system will be an expansion of Monoidal t-norm-based logic. First, we introduce an infinitary axiomatic system \(\mathsf {L}_*^\infty \), expanding the language with \(\Delta \) and countably many truth constants, and with only one infinitary inference rule, that is inspired in Takeuti–Titani density rule. Then we show that \(\mathsf {L}_*^\infty \) is indeed strongly complete with respect to the standard algebra
This system will be an expansion of Monoidal t-norm-based logic. First, we introduce an infinitary axiomatic system \(\mathsf {L}_*^\infty \), expanding the language with \(\Delta \) and countably many truth constants, and with only one infinitary inference rule, that is inspired in Takeuti–Titani density rule. Then we show that \(\mathsf {L}_*^\infty \) is indeed strongly complete with respect to the standard algebra  . Moreover, the approach is generalized to axiomatize expansions of these logics with additional operators whose intended semantics over [0, 1] satisfy some regularity conditions.
. Moreover, the approach is generalized to axiomatize expansions of these logics with additional operators whose intended semantics over [0, 1] satisfy some regularity conditions.

Similar content being viewed by others
Notes
As it is usual in the literature, the symbol \(\Delta \) denotes both the connective in the language and the corresponding operation in the algebra, as it happens with \(\wedge \) and \(\vee \).
The \(\Delta \) connective is used to prove semilinearity of the axiomatic system.
This is simply a subset, closed under substitutions, of \(\{ \langle \Gamma , \varphi \rangle : \Gamma \cup \{\varphi \} \subseteq Fm \}\). Notice that we allow rules with infinite premises \(\Gamma \).
Let us stress that we do not consider the smallest consequence operator closed under substitutions.
Let us point out that indeed this condition implies that for every natural number \(m \leqslant n\), it holds that either
-
\(\xi _m \in \Sigma _{n+1}\), or
-
\(\lnot \Delta \xi _m \in \Sigma _{n+1}\) and there is some \(\psi \in \Phi _m\) such that \(\lnot \Delta \psi \in \Sigma _{n+1}\).
Notice that this last disjunction is capturing the intuition that \(\Sigma _{n+1}\) (and all its extensions) is a model of all the derivations in \(\langle (\Phi _{m}, \xi _{m}): m \leqslant n \rangle \).
-
This finiteness is employed to show that for each rule in the axiomatic system, there is at most a countable number of substitutions.
If for all two constants like above \(d_1 *d_2 \leqslant c\), applying residuation \(d_1 \leqslant d_2 \rightarrow c\) and so the supremum can be taken in the left side. Similarly, we get that \(\sup \mathcal {C}^-_a *\sup \mathcal {C}^-_b \leqslant c\) which contradicts the assumptions.
This can be also seen as a direct consequence of the fact that all \(L_*^\infty \)-chains are relatively simple.
For the reader interested in checking the details we suggest to start considering the following three elements in \(\varvec{A}\):
$$\begin{aligned} t_1:=\left( \frac{1}{2}\right) _{q \in [0,1)_\mathbb {Q}} \quad t_2:=(\widetilde{q})_{q \in [0,1)_\mathbb {Q}} \quad t_3:=(q)_{q \in [0,1)_\mathbb {Q}} \end{aligned}$$and checking that all possible combinations of these three elements under \(\wedge , \vee , \rightarrow , \Delta \) are also elements in our universe A. Indeed, all difficulties to provide a general proof that A is closed under the operations are illustrated in the previous particular case.
With the notation \(x \leqslant r \uparrow \) we mean that \(x \leqslant \overline{c}^{\varvec{A}}\) for every \(c \in (r,1]_\mathbb {Q}\). In an analogous way, \(r \downarrow \leqslant x\) stands for \(\overline{c}^{\varvec{A}} \leqslant x\) for all \(c \in [0,r)_\mathbb {Q}\).
As expected, \(\Upsilon _i^f(\vec {\varphi })\) stands for \(\{\lambda (\vec {\varphi })\}_{\lambda \in \Upsilon _i}\), and \(\vec {e(\varphi )} = \langle e(\varphi _1), \ldots e(\varphi _n) \rangle \).
Observe that if component k of region \(R_i\) has only one point, these premises are never met. Thus, the rule associated to that pair of region and component is equivalent to the rule \(\overline{0} \vdash \vartheta \), and so, it will not be used in order to “compute” the value of the function in that point (this will be done with a different component or a book-keeping axiom, depending on the case).
As already mentioned before concerning operations with regions with smaller dimensions, at this point of the proof, if f was an operation such that \(\{d \in A: (\Upsilon _i^f)^{\varvec{A}}(\langle \vec {b}, d \rangle _k \in \mathrm{{Int}}_f(R_i) \text { for some } \vec {b} \in A^{n}\} = \{\overline{c_0}^{\varvec{A}}\}\) for some \(c_0 \in \mathbb {Q}_*^{\mathrm{{OP}}}\), the proof would finish here. Indeed, \(c_0\) in \(C_1\) by definition, and so trivially \( \overline{f}^{\varvec{A}}(\overline{c_0}^{\varvec{A}}, a_2) \leqslant \sup \{\overline{f}^{\varvec{A}}(\overline{c}^{\varvec{A}}, a_2): c \in [0,b]_\mathbb {Q}, \overline{c}^{\varvec{A}} \leqslant a_1\} \).
This set is non-empty: \(x_1 > 0\) because \((\Upsilon _1^g)^{\varvec{A}}(x_1, x_2) = \{\overline{1}^{\varvec{A}}\}\) and the constants are dense in A.
Nevertheless, the case of the left-continuous t-norm operation \(*\) has a more direct proof, not needing any of the
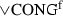 , \(\mathrm {\vee M^{f U}_{\langle i,k\rangle }}\) nor
, \(\mathrm {\vee M^{f U}_{\langle i,k\rangle }}\) nor  rules, relying on the MTL-axiomatization of a residuated operation, as we saw in Lemma 4.7.
rules, relying on the MTL-axiomatization of a residuated operation, as we saw in Lemma 4.7.
References
Agliano P, Montagna F (2003) Varieties of BL-algebras. I. General properties. J Pure Appl Algebra 181(2–3):105–129
Blok WJ, Pigozzi D (1989) Algebraizable logics, vol 396. Memoirs of the American Mathematical Society AMS, Providence
Bou F, Esteva F, Godo L, Rodríguez R (2011) On the minimum many-valued modal logic over a finite residuated lattice. J Logic Comput 21(5):739–790
Cignoli R, Esteva F, Godo L, Torrens A (2000) Basic fuzzy logic is the logic of continuous t-norms and their residua. Soft Comput 4(2):106–112
Cintula P (2004) From fuzzy logic to fuzzy mathematics. Ph.D. thesis, Czech Technical University in Prague
Cintula P (2016) A note on axiomatizations of Pavelka-style complete fuzzy logics. Fuzzy Sets Syst 292:160–174
Cintula P, Noguera C (2010) Implicational (semilinear) logics I: a new hierarchy. Arch Math Logic 49(4):417–446
Cintula P, Noguera C (2013) The proof by cases property and its variants in structural consequence relations. Studia Logica 101(4):713–747
Cintula P, Hájek P, Noguera C (eds) (2011) Handbook of mathematical fuzzy logic (in 2 volumes), volume 37 and 38 of studies in logic, mathematical logic and foundation. College Publications, London
Esteva F, Godo L (2001) Monoidal t-norm based logic: towards a logic for left-continuous t-norms. Fuzzy Sets Syst 124:271–288
Esteva F, Godo L, Montagna F (2004) Equational characterization of the subvarieties of BL generated by t-norm algebras. Studia Logica 76(2):161–200
Givant S, Halmos P (2009) Introduction to boolean algebras. Undergraduate texts in mathematics. Springer, Berlin
Hájek P (1998) Metamathematics of fuzzy logic, volume 4 of trends in logic. Studia Logica Library. Kluwer Academic Publishers, Dordrecht
Haniková Z (2014) Varieties generated by standard BL-algebras. Order 31(1):15–33
Jenei S, Montagna F (2002) A proof of standard completeness for Esteva and Godo’s logic MTL. Studia Logica 70:183–192
Montagna F (2007) Notes on strong completeness in Łukasiewicz, product and BL logics and in their first-order extensions. In: Algebraic and proof-theoretic aspects of non-classical logics: papers in honor of Daniele Mundici on the occasion of his 60th birthday, LNCS, vol 4460. Springer, pp 247–274
Pavelka J (1979a) On fuzzy logic. I. Many-valued rules of inference. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 25(1):45–52
Pavelka J (1979b) On fuzzy logic. II. Enriched residuated lattices and semantics of propositional calculi. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik. 25(2):119–134
Pavelka J (1979c) On fuzzy logic. III. Semantical completeness of some many-valued propositional calculi. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 25(5):447–464
Takeuti G, Titani S (1984) Intuitionistic fuzzy logic and intuitionistic fuzzy set theory. J Symb Logic 49(3):851–866
Vidal A, Esteva F, Godo L (2016) On modal extensions of product fuzzy logic. J Logic Comput. doi:10.1093/logcom/exv046 (in press)
Vidal A, Godo L, Esteva F (2015) On strongly standard complete fuzzy logics: \({MTL}^{Q}_*\) and its expansions. In: Alonso JM, Bustince H, Reformat M (eds) Proceedings of the IFSA-EUSFLAT-15, Gijón, Spain. Atlantis Press, pp 828–835
Acknowledgments
The authors are thankful to an anonymous reviewer for his/her comments that have helped to improve the final layout of this paper. Vidal has been supported by the joint project of Austrian Science Fund (FWF) I1897-N25 and Czech Science Foundation (GACR) 15-34650L and by the institutional support RVO:67985807. Esteva and Godo have been funded by the FEDER/MINECO Spanish Project TIN2015-71799-C2-1-P and by the Grant 2014SGR-118 from the Catalan Government. Bou thanks the Grant 2014SGR-788 from the Catalan Government.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Human and animal rights
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Communicated by A. Di Nola, D. Mundici, C. Toffalori, A. Ursini.
This paper is dedicated to the memory of Professor Franco Montagna, an excellent researcher and better person to whom these authors will always be indebted to. He has been a pioneer in many research areas (not only in MFL), and among such pioneering contributions we can find his work on infinitary axiomatic systems for standard $$\mathsf {BL}$$ BL -algebras. The present paper has been inspired by the novel ideas introduced by Franco on that topic.
This is an expanded and fully revised version of the conference paper (Vidal et al. 2015). In particular some proofs have become more cumbersome than were presumed there.
Rights and permissions
About this article
Cite this article
Vidal, A., Bou, F., Esteva, F. et al. On strong standard completeness in some MTL\(_\Delta \) expansions. Soft Comput 21, 125–147 (2017). https://doi.org/10.1007/s00500-016-2338-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-016-2338-0



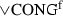 ,
,  rules, relying on the MTL-axiomatization of a residuated operation, as we saw in Lemma
rules, relying on the MTL-axiomatization of a residuated operation, as we saw in Lemma