Skip to main content
SpringerLink
Log in

Algebraic solution of fuzzy linear system as: \(\widetilde{A} \widetilde{X}+ \widetilde{B} \widetilde{X}=\widetilde{Y}\)

  • Methodologies and Application
  • Published:
Soft Computing Aims and scope Submit manuscript

Abstract

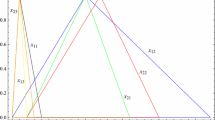
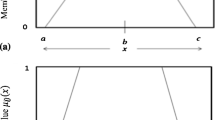
In this paper, fuzzy linear system as \(\widetilde{A} \widetilde{X}+ \widetilde{B} \widetilde{X}=\widetilde{Y}\) in which \(\widetilde{A}, \widetilde{B}\) are \(n \times n\) fuzzy matrices and \(\widetilde{X}, \widetilde{Y}\) are \(n \times 1\) fuzzy vectors is studied. A new method to solve such systems based on interval linear system, interval inclusion linear system is proposed. Numerical examples are given to illustrate the ability of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Abbasbandy S, Ezzati R, Jafarian A (2006) LU decomposition method for solving fuzzy system of equations. Appl Math Comput 172:633–643

    MATH  MathSciNet  Google Scholar 

  • Abbasbandy S, Jafarian A (2006) Steepest decent method for system of fuzzy linear equations. Appl Math Comput 175:823–833

    MATH  MathSciNet  Google Scholar 

  • Allahviranloo T (2004) Numerical methods for fuzzy system of linear equations. Appl Math Comput 155:493–502

    MATH  MathSciNet  Google Scholar 

  • Allahviranloo T (2005) Successive over relaxation iterative method for fuzzy system of linear equations. Appl Math Comput 162:189–196

    MATH  MathSciNet  Google Scholar 

  • Allahviranloo T, Salahshour S, Khezerloo M (2011) Maximal- and minimal symmetric solutions of fully fuzzy linear systems. J Comput Appl Math 235:4652–4662

    Article  MATH  MathSciNet  Google Scholar 

  • Allahviranloo T, Lotfi FH, Kiasari MK, Khezerloo M (2012) On the fuzzy solution of LR fuzzy linear systems. Appl Math Model 37(3):1170–1176

    Article  MATH  MathSciNet  Google Scholar 

  • Allahviranloo T, Ghanbari M (2012) On the algebraic solution of fuzzy linear systems based on interval theory. Appl Math Model 36(11):5360–5379

    Article  MATH  MathSciNet  Google Scholar 

  • Babakordi F, Allahviranlooa T, Adabitabar firozja M (2016) An efficient method for solving LR fuzzy dual matrix systems. J Intell Fuzzy Syst 30:575–581

    Article  MATH  Google Scholar 

  • Friedman M, Ming M, Kandel A (1998) Fuzzy linear systems. Fuzzy Sets Syst 96:201–209

    Article  MATH  MathSciNet  Google Scholar 

  • Kaur J, Kumar A (2013) Mehar’s method for solving fully fuzzy linear programming problems with LR fuzzy parameters. Appl Math Model 37:7142–7153

    Article  MathSciNet  Google Scholar 

  • Kumar A, Kaur J, Singh P (2011) A new method for solving fully fuzzy linear programming problems. Appl Math Model 35:817–823

    Article  MATH  MathSciNet  Google Scholar 

  • Neetu A, Kumar A, Bansal A (2013) Solving a fully fuzzy linear system with arbitrary triangular fuzzy numbers. Soft Comput 17:691–702

    Article  MATH  Google Scholar 

  • Seikkala S (1987) On the fuzzy initial value problem. Fuzzy Sets Syst 24:319–330

    Article  MATH  MathSciNet  Google Scholar 

  • Zimmermann HJ (1996) Fuzzy set theory and its applications, 3rd edn. Kluwer Academic, Norwell

    Book  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Science and Research Branch, Islamic Azad University, Tehran, Iran

    T. Allahviranloo

  2. Department of Mathematics, Gonbad Kavous University, Gonbad Kavous, Iran

    F. Babakordi

Authors
  1. T. Allahviranloo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. F. Babakordi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to F. Babakordi.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Communicated by V. Loia.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Allahviranloo, T., Babakordi, F. Algebraic solution of fuzzy linear system as: \(\widetilde{A} \widetilde{X}+ \widetilde{B} \widetilde{X}=\widetilde{Y}\) . Soft Comput 21, 7463–7472 (2017). https://doi.org/10.1007/s00500-016-2294-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00500-016-2294-8

Keywords

Search

Navigation