Abstract
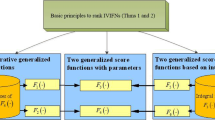
Fuzzy numbers and intuitionistic fuzzy numbers are introduced in the literature to model problems involving incomplete and imprecise numerical quantities. Researchers from all over the world have been working in ranking of intuitionistic fuzzy numbers since 1985, but till date there is no common methodology that rank any two arbitrary intuitionistic fuzzy numbers. In order to improve the familiar ranking methods, a new non-hesitance score function for the theory of interval-valued intuitionistic fuzzy sets is introduced and the necessity for defining a new non-hesitance score function is explained using illustrative examples. In this paper, a new multi-criteria decision-making algorithm is established for decision problems involving interval-valued intuitionistic fuzzy numbers. Further the practicality of the proposed method is shown by solving an interval-valued intuitionistic fuzzy MCDM problem. Finally, an illustrative example is given to demonstrate the practicality and effectiveness of the proposed approach.
Similar content being viewed by others
References
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96
Atanassov KT (2014) Index matrices: towards an augmented matrix calculus. Springer, Cham
Herrera F, Herrera-Viedma E (2000) Linguistic decision analysis: steps for solving decision problems under linguistic information. Fuzzy Sets Syst 115:67–82
Nayagam VLG, Muralikrishnan S, Sivaraman G (2011) Multi criteria decision making method based on interval valued intuitionistic fuzzy sets. Exp Syst Appl 38(3):1464–1467
Sahin R (2015) Fuzzy multicriteria decision making method based on the improved accuracy function for interval-valued intuitionistic fuzzy sets. Soft Comput 20(7):2557–2563
Xu ZS (2007) Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making. Control Decis 22(2):215–219
Xu ZS (2013) Intuitionistic fuzzy aggregation and clustering. Springer, Berlin
Yang Y, Liang C, Ji S (2015) Comments on fuzzy multicriteria decision making method based on the improved accuracy function for interval-valued intuitionistic fuzzy sets by Ridvan Sahin. Soft Comput. doi:10.1007/s00500-015-1988-7
Ye J (2009) Multicriteria fuzzy decision making method based on a novel accuracy function under interval-valued intuitionistic fuzzy environment. Exp Syst Appl 36(6):6899–6902
Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–356
Zhang F, Xu S (2015) Remarks to fuzzy multicriteria decision making method based on the improved accuracy function for interval-valued intuitionistic fuzzy sets. Soft Comput. doi:10.1007/s00500-015-1932-x
Acknowledgments
The authors are grateful to the anonymous reviewers whose thoughtful remarks are greatly useful for the improvement of the paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Communicated by V. Loia.
Rights and permissions
About this article
Cite this article
Nayagam, V.L.G., Jeevaraj, S. & Dhanasekaran, P. An intuitionistic fuzzy multi-criteria decision-making method based on non-hesitance score for interval-valued intuitionistic fuzzy sets. Soft Comput 21, 7077–7082 (2017). https://doi.org/10.1007/s00500-016-2249-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-016-2249-0