Skip to main content
SpringerLink
Log in

Impartial Digraphs

  • Published:
Combinatorica Aims and scope Submit manuscript

Abstract

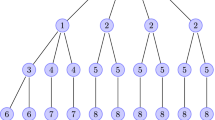
We prove a conjecture of Fox, Huang, and Lee that characterizes directed graphs that have constant density in all tournaments: they are disjoint unions of trees that are each constructed in a certain recursive way.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. O. Antolín Camarena, E. Csóka, T. Hubai, G. Lippner and L. Lovász: Positive graphs, European J. Combin. 52 (2016), 290–301.

    Article  MathSciNet  Google Scholar 

  2. D. Conlon, J. Fox and B. Sudakov: An approximate version of Sidorenko’s conjecture, Geom. Funct. Anal. 20 (2010), 1354–1366.

    Article  MathSciNet  Google Scholar 

  3. D. Conlon, J. H. Kim, C. Lee and J. Lee: Some advances on Sidorenko’s conjecture, J. Lond. Math. Soc. 98 (2018), 593–608.

    Article  MathSciNet  Google Scholar 

  4. D. Conlon and J. Lee: Sidorenko’s conjecture for blow-ups, Discrete Anal., to appear.

  5. D. Conlon and J. Lee: Finite reflection groups and graph norms, Adv. Math. 315 (2017), 130–165.

    Article  MathSciNet  Google Scholar 

  6. L. N. Coregliano and A. A. Razborov: On the density of transitive tournaments, J. Graph Theory 85 (2017), 12–21.

    Article  MathSciNet  Google Scholar 

  7. P. Diaconis and S. Janson: Graph limits and exchangeable random graphs, Rend. Mat. Appl. 28 (2008), 33–61.

    MathSciNet  MATH  Google Scholar 

  8. P. Erdős and M. Simonovits: Supersaturated graphs and hypergraphs, Combinatorica 3 (1983), 181–192.

    Article  MathSciNet  Google Scholar 

  9. H. Hatami: Graph norms and Sidorenko’s conjecture, Israel J. Math. 175 (2010), 125–150.

    Article  MathSciNet  Google Scholar 

  10. J. H. Kim, C. Lee and J. Lee: Two approaches to Sidorenko’s conjecture, Trans. Amer. Math. Soc. 368 (2016), 5057–5074.

    Article  MathSciNet  Google Scholar 

  11. J. L. X. Li and B. Szegedy: On the logarithimic calculus and Sidorenko’s conjecture, arXiv:1107.1153.

  12. L. Lovász: Large networks and graph limits, American Mathematical Society Colloquium Publications, vol. 60, American Mathematical Society, Providence, RI, 2012.

    MATH  Google Scholar 

  13. L. Lovász and B. Szegedy; Regularity partitions and the topology of graphons, An irregular mind, Bolyai Soc. Math. Stud., vol. 21, János Bolyai Math. Soc., Budapest, 2010, 415–446.

    MATH  Google Scholar 

  14. MathOverflow: https://mathoverflow.net/q/189222.

  15. A. Sah, M. Sawhney, D. Stoner and Y. Zhao; A reverse Sidorenko inequality, Invent. Math., to appear.

  16. A. Sidorenko: A correlation inequality for bipartite graphs, Graphs Combin. 9 (1993), 201–204.

    Article  MathSciNet  Google Scholar 

  17. B. Szegedy: An information theoretic approach to Sidorenko’s conjecture, arXiv:1406.6738.

  18. E. Thörnblad: Decomposition of tournament limits, European J. Combin. 67 (2018), 96–125.

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

We thank the anonymous referees for careful readings and helpful comments.

Author information

Authors and Affiliations

  1. Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA, USA

    Yufei Zhao

  2. Department of Mathematics, Stanford University, Stanford, CA, USA

    Yunkun Zhou

Authors
  1. Yufei Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yunkun Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yufei Zhao.

Additional information

Zhao was supported by NSF Awards DMS-1362326 and DMS-1764176, the MIT Solomon Buchsbaum Fund, and a Sloan Research Fellowship. Zhou was supported by the MIT Undergraduate Research Opportunities Program.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, Y., Zhou, Y. Impartial Digraphs. Combinatorica 40, 875–896 (2020). https://doi.org/10.1007/s00493-020-4280-0

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00493-020-4280-0

Mathematics Subject Classification (2010)

Search

Navigation