A conceptual stochastic rainfall-runoff model of an order-one catchment under a stationary precipitation regime

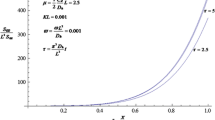
Abstract

We derive and solve a linear stochastic model for the evolution of discharge and runoff in an order-one watershed. The system is forced by a statistically stationary compound Poisson process of instantaneous rainfall events. The relevant time scales are hourly or larger, and for large times, we show that the discharge approaches a limiting invariant distribution. Hence any of its properties are with regard to a rainfall-runoff system in hydrological equilibrium. We give an explicit formula for the Laplace transform of the invariant density of discharge in terms of the catchment area, the residence times of water in the channel and the hillslopes, and the mean frequency and the probability distribution of rainfall inputs. As a study case, we consider a watershed under a stationary rainfall regime in the tropical Andes of Colombia and test the probability distribution predicted by the model against the corresponding seasonal statistics. A mathematical analysis of the invariant distribution is performed yielding formulas for the invariant moments of discharge in terms of those of the rainfall. The asymptotic behavior of the probabilities of extreme discharge events is explicitly derived for heavy-tailed and light-tailed families of distributions of rainfall inputs. The scaling structure of discharge is asymptotically characterized in terms of the parameters of the model and under the assumption of wide sense scaling for the precipitation amounts and the inverse of the residence time in the channel. Our results give insights into the conversion of uncertainty inherent to the rainfall-runoff dynamics and the roles played by different geophysical variables, with the ratio between the mean frequency of rainfall events to the residence time along the hillslopes largely determining the qualitative properties of the distribution of discharge.

Appendix

Here we summarize some of the mathematical results used in Sect. 5 to infer information about a distribution given the Laplace transform of its probability density function. We begin with the main result on the existence and characterization of invariant distributions for processes of the Ornstein-Uhlembeck Type applied to ${\varvec{X}}$ in (8)

Theorem 1

(Sato and Yamazato (1984)) A necessary and sufficient condition for the existence of a unique invariant density for ${\varvec{X}}$ is

$$\begin{aligned} \int _1^{\infty } \log (y) f(y) \, \mathrm {d}y < \infty . \end{aligned}$$

(37)

If (37) holds, then the distribution of ${\varvec{X}}(t)$ converges weakly to a distribution with Laplace transform given by

$$\begin{aligned} {\tilde{\varvec{g}}}_{{\varvec{X}}}(s_1,s_2) = \exp \left\{ -\frac{\lambda }{H} \int _0^{1} \!\! \frac{1-\tilde{f}(a H (s_2 u + s_1 m(u))}{u} \, \mathrm {d}u \right\} , \end{aligned}$$

(38)

where f is the common density of rainfall amounts, $\tilde{f}$ its Laplace transform, and the function m(u) is given by Eq. 13

Moreover, the process ${\varvec{X}}$ is ergodic, and $\varvec{g}_{{\varvec{X}}}$ is its unique invariant density. See also Konecny (1992) and Ramirez and Constantinescu (2020).

Note that the Laplace transform in (38) is bi-dimensional, $\tilde{g}_{{\varvec{X}}}(s_1,s_2) = {\mathbb{E}}_g e^{s_1Q+ s_2 R}$. The Laplace transform in Eq. (14), of the invariant density for Q, is obtained as $\tilde{g}(s) = \tilde{g}_{{\varvec{X}}}(0,s)$.

We now turn to the partial characterization of the threshold value $\eta _c = 1$ mentioned in Sect. 3.2.

Theorem 2

Suppose the distribution of P satisfies (37) and let g be the probability density of Q. Then, if $0<\eta < 1$, $\lim _{x \rightarrow 0^+} g(x) = 0$.

Proof

It suffices to prove that $\gamma (x) \rightarrow 0$ as $x \rightarrow 0$, which by the initial value theorem is equivalent to proving $s \tilde{\gamma }(s) \rightarrow 0$ as $s \rightarrow \infty$ (see for example Beerends et al. 2003). Since $\tilde{\phi }(s) = {\mathbb{E}}e^{-s P}$, Jensen’s inequality ensures that $\tilde{\phi }(s) \ge e^{-s}$ for all s. Moreover $m(u) \le m_0(u) := \frac{u}{1-\beta }$ for $0\le u \le 1$. We thus get the following bound

$$\begin{aligned} s\tilde{\gamma }(s) \le s \exp \left\{ - \int _0^1 \frac{1-e^{-s \eta m_0(u)}}{\eta u}\, \mathrm {d}u \right\} \\ = s \exp \left\{ -\frac{1}{\eta } \left( \gamma _e - \text {Chi}\left( \frac{s \eta }{\beta -1} \right) + \text {Shi}\left( \frac{s \eta }{\beta -1} \right) \right. \right. \\ \left. \left. + \log \left( \frac{s \eta }{-\beta } \right) \right) \right\} , \end{aligned}$$

(39)

where $\gamma _e$ denotes the Euler gamma constant, and Shi and Chi are the hyperbolic sine and hyperbolic cosine integral functions, respectively. The function on the right-hand side of (1) converges to zero if $0<\eta <1$ and diverges to infinity for $\eta >1$. $\square$

The characterization of the asymptotic behavior of ${{\mathbb{P}}}(Q>x)$ given in Subsect. 5.2 rests upon two mathematical results. The first is an application of the‘Karamata Tauberian Theorem’ and the ‘Monotone Density Theorem’. See Bingham et al. (1989), theorems 1.7.1, 1.7.2, and Ramirez and Constantinescu (2020) for complete details. Equation 24 for the Pareto distributed rainfall follows from explicitly computing the integral in (14) and a direct application of the following Theorem 3

Theorem 3

Let X be a positive random variable with probability density function f having Laplace transform $\tilde{f}(s) = \exp (-h(s))$ with $h(s) \sim c s^{\rho }$ as $s \rightarrow 0^+$ for some $\rho >0$. Then ${{\mathbb{P}}}(X>x) \sim \frac{c}{\Gamma (1-\rho )} x^{-\rho }$ as $x \rightarrow \infty$.

Proof

G(x) is a positive function with Laplace transform $\tilde{G}(s) = \frac{1}{s}(1-\tilde{f}(s))$ which by a Taylor expansion decays as $\tilde{G}(s) \sim c s^{\rho -1}$. The Karamata Tauberian Theorem yields $\int _0^x G(y) \, \mathrm {d}y \sim \frac{c}{\Gamma (2-\rho )} x^{1-\rho }$ as $x\rightarrow \infty$. Differentiating via the Monotone Density Theorem gives the desired result. $\square$

The result (26) for the Gamma distributed rainfall requires a subtler approach for which we follow Nakagawa (2005). Let f be a function with Laplace transform $\tilde{f}(s)=\int _0^\infty f(x) e^{-s x} \, \mathrm {d}x$ with $s = \sigma +i \tau$. We say that $\sigma _0$ is the abscissa of convergence of $\tilde{f}$ if the integral converges for $\sigma >\sigma _0$ and diverges for $\sigma <\sigma _0$. For example, the abscissa of convergence for the probability density function of a Gamma$(\omega ,\rho )$ distribution is $\sigma _0 = -1/\rho$.

Theorem 4

(Nakagawa (2005), Theorem 1) For a non-negative random variable X with density function f(x), let $-\xi$ be the abscissa of convergence of $\tilde{f}(s)$. If $\xi >0$ and $s=-\xi$ is a pole for $\tilde{f}$, then:

$$\begin{aligned} \lim _{x \rightarrow +\infty } \frac{1}{x} \log {{\mathbb{P}}}(X > x)= -\xi \end{aligned}$$

(40)

In the notation introduced in Sect. 5, equation (40) is written ${{\mathbb{P}}}(X>x) \simeq e^{-\xi }$. Note that applying L’Hospital rule twice on the limit (40) yields $f'(x)/f(x) = -\xi + o(1)$, which implies that $f(x) = c_0 e^{-\xi x + o(1/x)}$ as $x \rightarrow \infty$ for some positive constant $c_0$.

Formula (26) for the asymptotic behavior of $P_g(Q>x)$ in the case of Gamma distributed P follows from performing the integral in (12), computing the abscissa of convergence,$s=-\xi$ and proving it is a pole for $\tilde{g}$. See Ramirez and Constantinescu (2020), Proposition 5.3.

Table 4 Mathematical notation