Skip to main content
SpringerLink
Log in

Recognizing groundwater DNAPL contaminant source and aquifer parameters using parallel heuristic search strategy based on Bayesian approach

  • Original Paper
  • Published:
Stochastic Environmental Research and Risk Assessment Aims and scope Submit manuscript

Abstract

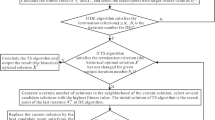
In this paper, a parallel heuristic search strategy based on Bayesian approach was first proposed for recognizing groundwater DNAPL contaminant source and aquifer parameters (unknown variables). Frequent calls to numerical simulation model effectuated large computational burden during likelihood calculation. Single surrogate system was established to reduce the burden, but it had unavoidable limitations. Thus, we first presented the particle swarm optimization-tabu search hybrid algorithm to construct an optimal combined surrogate system for the simulation model, which assembled Gaussian process, kernel extreme learning machine, support vector regression, and also improved the accuracy of the surrogate system to simulation model. Thereafter, a parallel heuristic search iterative process was first implemented for simultaneous recognition of unknown variables. Each round of iteration involved determination of candidate points and state transitions. The Monte Carlo approach was used widely for selecting candidate point, but it did not readily converge to posterior distribution when the probability density functions were complex. And the search ergodicity was weak. In order to improve the search ergodicity, a DE algorithm with variable mutation rate based on rand-to-best, 1, and bin strategy was first proposed in this paper to determine multiple candidate points. The recognition results were obtained when the iteration process terminated. The accuracy and efficiency of our approaches were demonstrated through a hypothetical case in DNAPLs-contaminated aquifer, and the recognizing accuracy was high. More importantly, the new simulation model based on the recognition results is helpful in calculating future contaminant plume in the aquifer, which can provide credible basis for groundwater contaminant remediation plan design and risk assessment.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Behzadian K, Kapelan Z, Savic D, Ardeshir A (2009) Stochastic sampling design using a multi-objective genetic algorithm and adaptive neural networks. Environ Modell Softw 24(4):530–541

    Google Scholar 

  • Braak CJT, Vrugt JA (2008) Differential evolution Markov chain with snooker updater and fewer chains. Stat Comput 18(4):435–446

    Google Scholar 

  • Chen C, Li W, Su H, Liu K (2014) Spectral-spatial classification of hyperspectral image based on kernel extreme learning machine. Remote Sens 6(6):5795–5814

    Google Scholar 

  • Cowles MK, Carlin BP (1996) Markov Chain Monte Carlo convergence diagnostics: a comparative review. J Am Stat Assoc 91(434):883–904

    Google Scholar 

  • Datta B, Chakrabarty D, Dhar A (2009) Simultaneous identification of unknown groundwater pollution sources and estimation of aquifer parameters. J Hydrol 376(1–2):48–57

    CAS  Google Scholar 

  • Datta B, Chakrabarty D, Dhar A (2011) Identification of unknown groundwater pollution sources using classical optimization with linked simulation. J Hydro Environ Res 5(1):25–36

    Google Scholar 

  • Delshad M, Pope GA, Sepehrnoori K (1996) A compositional simulator for modeling surfactant enhanced aquifer remediation, 1. Formul J Contam Hydrol 23(4):303–327

    CAS  Google Scholar 

  • Gelman A, Rubin DB (1992) Inference from iterative simulation using multiple sequences. Stat Sci 7(4):457–472

    Google Scholar 

  • Gorelick SM, Evans B, Remson I (1983) Identifying sources of groundwater pollution: an optimization approach. Water Resour Res 19(3):779–790

    CAS  Google Scholar 

  • Guozhen W, Zhang C, Li Y, Haixing L, Zhou H (2016) Source identification of sudden contamination based on the parameter uncertainty analysis. J Hydroinform 18(6):919–927

    Google Scholar 

  • Haario H, Saksman E, Tamminen J (1999) Adaptive proposal distribution for random walk Metropolis algorithm. Comput Stat 14(3):375–396

    Google Scholar 

  • Haario H, Saksman E, Tamminen J (2001) An adaptive Metropolis algorithm. Bernoulli 7(2):223–242

    Google Scholar 

  • Haario H, Laine M, Mira A, Saksman E (2006) DRAM: efficient adaptive MCMC. Stat Comput 16(4):339–354

    Google Scholar 

  • He L, Huang GH, Lu HW (2010) A stochastic optimization model under modeling uncertainty and parameter certainty for groundwater remediation design-part I. Model development. J Hazard Mater 176(1–3):521–526

    CAS  Google Scholar 

  • Hou Z, Lu W (2018) Comparative study of surrogate models for groundwater contamination source identification at DNAPL-contaminated sites. Hydrogeol J 26(3):923–932

    Google Scholar 

  • Hou Z, Lu W, Chu H, Luo J (2015) Selecting parameter-optimized surrogate models in DNAPL-contaminated aquifer remediation strategies. Environ Eng Sci 32(12):1016–1026

    CAS  Google Scholar 

  • Hou Z, Lu W, Xue H, Lin J (2017) A comparative research of different ensemble surrogate models based on set pair analysis for the DNAPL-contaminated aquifer remediation strategy optimization. J Contam Hydrol 203:28–37

    CAS  Google Scholar 

  • Hu JN, Hu JJ, Lin HB, Li XP, Jiang CL, Qiu XH, Li WS (2014) State-of-charge estimation for battery management system using optimized support vector machine for regression. J Power Sour 269:682–693

    CAS  Google Scholar 

  • Janusevskis J, Le Riche R (2012) Simultaneous kriging-based estimation and optimization of mean response. J Glob Optim 55(2):313–336

    Google Scholar 

  • Jiang X, Lu W, Hou Z, Zhao H, Na J (2015) Ensemble of surrogates-based optimization for identifying an optimal surfactant-enhanced aquifer remediation strategy at heterogeneous DNAPL-contaminated sites. Comput Geosci 84:37–45

    CAS  Google Scholar 

  • Kazemi Nia Korrani A, Sepehrnoori K, Delshad M (2015) Coupling IPhreeqc with UTCHEM to model reactive flow and transport. Comput Geosci 82:152–169

    CAS  Google Scholar 

  • Laloy E, Vrugt JA (2012) High-dimensional posterior exploration of hydrologic models using multiple-try DREAM(ZS) and high-performance computing. Water Resour Res 50(3):182–205

    Google Scholar 

  • Laloy E, Rogiers B, Vrugt JA, Mallants D, Jacques D (2013) Efficient posterior exploration of a high-dimensional groundwater model from two-stage Markov chain Monte Carlo simulation and polynomial chaos expansion. Water Resour Res 49(5):2664–2682

    Google Scholar 

  • Lapworth DJ, Baran N, Stuart ME, Ward RS (2012) Emerging organic contaminants in groundwater: a review of sources, fate and occurrence. Environ Pollut 163:287–303

    CAS  Google Scholar 

  • Li M, Huang X, Liu H, Liu B, Wu Y, Xiong A, Dong T (2013) Prediction of gas solubility in polymers by back propagation artificial neural network based on self-adaptive particle swarm optimization algorithm and chaos theory. Fluid Phase Equilibr 356:11–17

    CAS  Google Scholar 

  • Lin HT, Tan YC, Chen CH, Yu HL, Wu SC, Ke KY (2010) Estimation of effective hydrogeological parameters in heterogeneous and anisotropic aquifers. J Hydrol 389(1–2):57–68

    Google Scholar 

  • Luo J, Lu W (2014) Comparison of surrogate models with different methods in groundwater remediation process. J Earth Syst Sci 123(7):1579–1589

    Google Scholar 

  • Luo J, Lu W, Xin X, Chu H (2013) Surrogate model application to the identification of an optimal surfactant-enhanced aquifer remediation strategy for DNAPL-contaminated sites. J Earth Sci 24(6):1023–1032

    Google Scholar 

  • Mirghani BY, Zechman EM, Ranjithan RS, Mahinthakumar G (2012) Enhanced simulation-optimization approach using surrogate modeling for solving inverse problems. Environ Forensics 13(4):348–363

    Google Scholar 

  • Prakash O, Datta B (2012) Sequential optimal monitoring network design and iterative spatial estimation of pollutant concentration for identification of unknown groundwater pollution source locations. Environ Monit Assess 185(7):5611–5626

    Google Scholar 

  • Shi X, Ye M, Curtis GP, Miller GL, Meyer PD, Kohler M, Yabusaki S, Wu J (2014a) Assessment of parametric uncertainty for groundwater reactive transport modeling. Water Resour Res 50(5):4416–4439

    Google Scholar 

  • Shi Y, Zhao LJ, Tang J (2014b) Recognition model based feature extraction and kernel extreme learning machine for high dimensional data. Adv Mater Res 875:2020–2024

    Google Scholar 

  • Srivastava D, Singh RM (2015) Groundwater system modeling for simultaneous identification of pollution sources and parameters with uncertainty characterization. Water Resour Manag 29(13):4607–4627

    Google Scholar 

  • Tan CC, Tung CP, Chen CH, Yeh WWG (2008) An integrated optimization algorithm for parameter structure identification in groundwater modeling. Adv Water Resour 31(3):545–560

    CAS  Google Scholar 

  • Vrugt JA, ter Braak CJF, Diks CGH, Robinson BA, Hyman JM, Higdon D (2009) Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling. Int J Non Sci Numer 10(3):273–290

    Google Scholar 

  • Wang X, Han M (2014) Online sequential extreme learning machine with kernels for nonstationary time series prediction. Neurocomputing 145:90–97

    Google Scholar 

  • Wang FK, Huang PR (2013) Implementing particle swarm optimization algorithm to estimate the mixture of two Weibull parameters with censored data. J Stat Comput Sim 84(9):1975–1989

    Google Scholar 

  • Wu SC, Tan YC, Chen CH, Lin ST, Ke KY (2008) A two-dimensional inverse model to identify transmissivity in an anisotropic aquifer. Hydrol Process 22(26):5086–5096

    Google Scholar 

  • Xing Z, Qu R, Zhao Y, Fu Q, Ji Y, Lu W (2019) Identifying the release history of a groundwater contaminant source based on an ensemble surrogate model. J Hydrol 572:501–516

    CAS  Google Scholar 

  • Yanai T, Nakano H, Nakajima T, Tsuneda T, Hirata S, Kawashima Y, Nakao Y, Kamiya M, Sekino H, Hirao K (2003) UTChem—a program for ab initio quantum chemistry. Comput Sci ICCS 2003:84–95

    Google Scholar 

  • Yao Y, Yang F, Suuberg EM, Provoost J, Liu W (2014) Estimation of contaminant subslab concentration in petroleum vapor intrusion. J Hazard Mater 279:336–347

    CAS  Google Scholar 

  • Zanini A, Woodbury AD (2016) Contaminant source reconstruction by empirical Bayes and Akaike’s Bayesian information criterion. J Contam Hydrol 185–186:74–86

    Google Scholar 

  • Zeng XK, Ye M, Wu JC, Wang D, Zhu XB (2018) Improved nested sampling and surrogate-enabled comparison with other marginal likelihood estimators. Water Resour Res 54(2):797–826

    Google Scholar 

  • Zhang Y, Kimberg DY, Coslett HB, Schwartz MF, Wang Z (2014) Multivariate lesion-symptom mapping using support vector regression. Hum Brain Mapp 35(12):5861–5876

    Google Scholar 

  • Zhang J, Zeng L, Chen C, Chen D, Wu L (2015) Efficient Bayesian experimental design for contaminant source identification. Water Resour Res 51(1):576–598

    Google Scholar 

  • Zhang J, Li W, Zeng L, Wu L (2016) An adaptive Gaussian process-based method for efficient Bayesian experimental design in groundwater contaminant source identification problems. Water Resour Res 52(8):5971–5984

    Google Scholar 

  • Zhang J, Li W, Lin G, Zeng L, Wu L (2017) Efficient evaluation of small failure probability in high-dimensional groundwater contaminant transport modeling via a two-stage Monte Carlo method. Water Resour Res 53(3):1948–1962

    Google Scholar 

  • Zhao Y, Lu W, An Y (2015) Surrogate model-based simulation-optimization approach for groundwater source identification problems. Environ Forensics 16(3):296–303

    Google Scholar 

  • Zhao Y, Lu W, Xiao C (2016) A Kriging surrogate model coupled in simulation-optimization approach for identifying release history of groundwater sources. J Contam Hydrol 185–186:51–60

    Google Scholar 

Download references

Acknowledgements

This research was supported by the National Natural Science Foundation of China (No. 41972252) and the National Key Research and Development Program of China (No. 2018YFC1800405).

Author information

Authors and Affiliations

  1. Key Laboratory of Groundwater Resources and Environment, Ministry of Education, Jilin University, Changchun, 130021, China

    Han Wang & Wenxi Lu

  2. Jilin Provincial Key Laboratory of Water Resources and Environment, Jilin University, Changchun, 130021, China

    Han Wang & Wenxi Lu

  3. College of New Energy and Environment, Jilin University, Changchun, 130021, China

    Han Wang & Wenxi Lu

Authors
  1. Han Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wenxi Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wenxi Lu.

Ethics declarations

Conflict of interest

We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the submitted manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, H., Lu, W. Recognizing groundwater DNAPL contaminant source and aquifer parameters using parallel heuristic search strategy based on Bayesian approach. Stoch Environ Res Risk Assess 35, 813–830 (2021). https://doi.org/10.1007/s00477-020-01909-7

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00477-020-01909-7

Keywords

Search

Navigation