Abstract
Resource estimation of mineral deposits requires spatial modelling of orebody boundaries based on a set of exploration borehole data. Given lateritic bauxite deposits, the spacing between the boreholes is often determined based on the grade continuity. As a result, the selected drill spacing might not capture the underlying (true) lateral variability apparent in the orebody boundaries. The purpose of this study is to investigate and address the limitations imposed by such problems in lateritic metal deposits through multiple-point statistics (MPS) framework. Rather than relying on a semivariogram model, we obtain the required structural information from the footwall topographies exposed after previous mining operations. The investigation utilising the MPS was carried out using the Direct Sampling (DS) MPS algorithm. Two historical mine areas along with their mined-out surfaces and ground penetrating radar surveys were incorporated as a bivariate training image to perform the MPS simulations. In addition, geostatistical simulations using the Turning Bands method were also performed to make the comparison against the MPS results. The performances were assessed using several statistical indicators including higher-order spatial cumulants. The results have shown that the DS can satisfactorily simulate the orebody boundaries by using prior information from the previously mined-out areas.

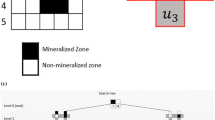
After Erten (2012)

After Erten (2012)











Similar content being viewed by others
References
Abzalov MZ, Bower J (2014) Geology of bauxite deposits and their resource estimation practices. Appl Earth Sci 123(2):118–134
Arpat GB, Caers J (2007) Conditional simulation with patterns. Math Geol 39(2):177–203
Bardossy G, Szabo IR, Varga G (2003) A new method of resource estimation for bauxite and other solid mineral deposits. Berg Und Huttenmannische Monatshefte 148(2):57–64
Bastante FG, Taboada J, Alejano L, Alonso E (2008) Optimization tools and simulation methods for designing and evaluating a mining operation. Stoch Environ Res Risk Assess 22(6):727–735
Bourassi A, Foucher B, Geffroy F, Marin JY, Martin B, Meric YM, Perseval S, Renard D, Robinot L, Touffait Y, Wagner L (2016) Isatis software user’s guide. Geovariances, Ecole des Mines de Paris, Paris
Dagasan Y (2018) Development of a grade control technique optimizing dilution and ore loss trade-off in lateritic bauxite deposits. PhD Thesis, Curtin University, Curtin
Dagasan Y, Erten O, Topal E (2018a) Accounting for a spatial trend in fine-scale ground-penetrating radar data: a comparative case study. J South Afr Inst Min Metall 118(2):173–184
Dagasan Y, Renard P, Straubhaar J, Erten O, Topal E (2018b) Automatic parameter tuning of multiple-point statistical simulations for lateritic bauxite deposits. Minerals 8:220
Dagasan Y, Renard P, Straubhaar J, Erten O, Topal E (2018c) Pilot point optimization of mining boundaries for lateritic metal deposits: Finding the trade-off between dilution and ore loss. Nat Resour Res 28:153–171
Davis JL, Annan AP (1989) Ground-penetrating radar for high-resolution mapping of soil and rock stratigraphy 1. Geophys Prospect 37(5):531–551
de Freitas Silva M, Dimitrakopoulos R (2016) Simulation of weathered profiles coupled with multivariate block-support simulation of the puma nickel laterite deposit, brazil. Eng Geol 215:108–121
De Iaco S, Maggio S (2011) Validation techniques for geological patterns simulations based on variogram and multiple-point statistics. Math Geosci 43(4):483–500
Dimitrakopoulos R (1998) Conditional simulation algorithms for modelling orebody uncertainty in open pit optimisation. Int J Surf Min Reclam Environ 12(4):173–179
Dimitrakopoulos R, Mustapha H, Gloaguen E (2010) High-order statistics of spatial random fields: exploring spatial cumulants for modeling complex non-gaussian and non-linear phenomena. Math Geosci 42(1):65–99
Erten O (2012) Profiling and mining control to mitigate dilution effect from SiO2 at the base of a bauxite deposit. PhD Thesis, School of Mechanical and Mining Engineering, The University of Queensland
Erten O, Kizil MS, Topal E, McAndrew L (2013) Spatial prediction of lateral variability of a laterite-type bauxite horizon using ancillary ground-penetrating radar data. Nat Resour Res 22(3):207–227
Erten O, McAndrew L, Kizil MS, Topal E (2015) Incorporating fine-scale ground-penetrating radar data into the mapping of lateral variability of a laterite-type bauxite horizon. Min Technol 124(1):1–15
Gloaguen E, Dimitrakopoulos R (2009) Two-dimensional conditional simulations based on the wavelet decomposition of training images. Math Geosci 41(6):679–701
Goodfellow R, Consuegra FA, Dimitrakopoulos R, Lloyd T (2012) Quantifying multi-element and volumetric uncertainty, coleman mccreedy deposit, ontario, canada. Comput Geosci 42:71–78
Guardiano FB, Srivastava RM (1992) Borrowing complex geometries from training images: the extended normal equations algorithm. Stanford Center for Reservoir Forecasting Report, Stanford University, Stanford
Hartman HL, Mutmansky JM (2002) Introductory mining engineering. Wiley, Hoboken
Honarkhah M, Caers J (2010) Stochastic simulation of patterns using distance-based pattern modeling. Math Geosci 42(5):487–517
Jones P, Douglas I, Jewbali A (2013) Modeling combined geological and grade uncertainty: application of multiple-point simulation at the apensu gold deposit, ghana. Math Geosci 45(8):949–965
Journel AG (2005) Beyond covariance: the advent of multiple-point geostatistics. Geostat Banff 2004:225–233
Mariethoz G, Caers J (2014) Multiple-point geostatistics: stochastic modeling with training images. Wiley, Hoboken
Mariethoz G, Renard P, Straubhaar J (2010) The direct sampling method to perform multiple-point geostatistical simulations. Water Resour Res 46(11):1–14
Matheron G (1973) The intrinsic random functions and their applications. Adv Appl Probab 5(3):439–468
Meerschman E, Pirot G, Mariethoz G, Straubhaar J, Van Meirvenne M, Renard P (2013) A practical guide to performing multiple-point statistical simulations with the direct sampling algorithm. Comput Geosci 52:307–324
Mery N, Emery X, Cáceres A, Ribeiro D, Cunha E (2017) Geostatistical modeling of the geological uncertainty in an iron ore deposit. Ore Geol Rev 88:336–351
Osterholt V, Dimitrakopoulos R (2018) Simulation of orebody geology with multiple-point geostatistics—application at yandi channel iron ore deposit, WA, and implications for resource uncertainty. In: Advances in applied strategic mine planning, Springer, New York, pp 335–352
Pasti HA, Costa JFCL, Boucher A (2012) Multiple-point geostatistics for modeling lithological domains at a Brazilian iron ore deposit using the single normal equations simulation algorithm. In: Geostatistics Oslo, Springer, New York, pp 397–407
Pérez C, Mariethoz G, Ortiz JM (2014) Verifying the high-order consistency of training images with data for multiple-point geostatistics. Comput Geosci 70:190–205
Renard D, Bez N, Desassis N, Beucher H, Ors F, Freulon X (2017) RGeostats: geostatistical package. http://cg.ensmp.fr/rgeostats. R package version 11.0.6. Accessed 3 Aug 2017
Rezaee H, Marcotte D (2017) Integration of multiple soft data sets in mps thru multinomial logistic regression: a case study of gas hydrates. Stoch Environ Res Risk Assess 31(7):1727–1745
Rezaee H, Mariethoz G, Koneshloo M, Asghari O (2013) Multiple-point geostatistical simulation using the bunch-pasting direct sampling method. Comput Geosci 54:293–308
Rezaee H, Marcotte D, Tahmasebi P, Saucier A (2015) Multiple-point geostatistical simulation using enriched pattern databases. Stoch Environ Res Risk Assess 29(3):893–913
Robles-Stefoni L, Dimitrakopoulos R (2016) Stochastic simulation of the fox kimberlitic diamond pipe, ekati mine, northwest territories, Canada. J South Afr Inst Min Metall 116(2):189–200
Rossi ME, Deutsch CV (2013) Mineral resource estimation. Springer, New York
Straubhaar J, Renard P, Mariethoz G, Froidevaux R, Besson O (2011) An improved parallel multiple-point algorithm using a list approach. Math Geosci 43(3):305–328
Strebelle S (2002) Conditional simulation of complex geological structures using multiple-point statistics. Math Geol 34(1):1–21
Tahmasebi P, Hezarkhani A, Sahimi M (2012) Multiple-point geostatistical modeling based on the cross-correlation functions. Comput Geosci 16(3):779–797
van der Grijp Y, Minnitt RCA (2015) Application of direct sampling multi-point statistic and sequential gaussian simulation algorithms for modelling uncertainty in gold deposits. J South Afr Inst Min Metall 115(1):73–85
Zhang T, Yi D, Huang T, Li X (2015) Reconstruction of porous media using multiple-point statistics with data conditioning. Stoch Environ Res Risk Assess 29(3):727–738
Zhang T, Switzer P, Journel A (2006) Filter-based classification of training image patterns for spatial simulation. Math Geol 38(1):63–80
Acknowledgements
The authors would like to thank Ilnur Minniakhmetov and Ryan Goodfellow from the Department of Mining and Materials Engineering of McGill University for providing the hosc software and their kind help.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Dagasan, Y., Erten, O., Renard, P. et al. Multiple-point statistical simulation of the ore boundaries for a lateritic bauxite deposit. Stoch Environ Res Risk Assess 33, 865–878 (2019). https://doi.org/10.1007/s00477-019-01660-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-019-01660-8