A multistage stochastic robust optimization model with fuzzy probability distribution for water supply management under uncertainty

Abstract

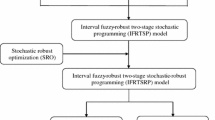
In this study, a fuzzy probability distribution- based multi-stage stochastic robust programming method has been developed for supporting regional water supply management. In the proposed model, methods of interval-parameter programming and robust stochastic optimization, and fuzzy probability distribution are introduced into a multi-stage stochastic programming framework, and the developed model can tackle uncertainties described in terms of interval values and fuzzy probability distributions. The developed model was applied to a water resources management system with three water users. A number of scenarios corresponding to different river inflow and α-cut levels are examined; the results suggest that reasonable solutions have been generated for regional water resources management. The results indicated that the optimization model’s outputs were highly dependent on the complex uncertain features of the study system, and the α-cut level of fuzzy probability had few significant impacts on the system objective. The results also implied that the developed method can be used for analyzing a variety of policy scenarios that are associated with different levels of economic consequences when the promised water-allocation targets are violated. Dynamics and uncertainties of water availability (and thus water allocation and shortage) could be taken into account through generation of a set of representative scenarios within a multistage context. The proposed method could be used by environmental managers to evaluate trade-offs of system benefits and risk involving fuzzy probability condition, as well as identify management solutions that sufficiently hedge against dual uncertainties.

Appendix

t	Planning period	i	Water user, i = 1,2,3,4 for municipal, industrial, agricultural and eco-environmental sector
k	Scenario of the happening of random events	h	Inflow level, h = 1,2,3 for low, medium, and high inflow level
L t	Length of planning period (year)	$W_{it}^{ \pm }$	Water allocation target (106 m3)
$RW_{it}^{ \pm }$	Reused water amount (106 m3)	$NB_{it}^{ \pm }$	Net benefit when water demand is satisfied ($/m3)
$\tilde{p}_{kt}$	Fuzzy probability of available water resources	$D_{ikt}^{ \pm }$	water deficit amount (106 m3)
$C_{it}^{ \pm }$	Penalty when water is not delivered ($/m3)	$CR_{it}^{ \pm }$	Cost for reused wastewater treatment ($/m3)
$\psi_{it}^{ \pm }$	Water production amount of per fresh water consumption	$WP_{th}^{ + }$	Available water resources amount (106 m3)
$DW_{it}^{ \pm }$	Water resources demand of each user (106 m3)	$SWT_{t}^{ \pm }$	Wastewater treatment capacity (106 m3)
$\xi_{it}^{ \pm }$	Wastewater reuse rate	$RWT_{it}^{ \pm }$	Reused water treatment capacity (106 m3)
$\omega$	Weight coefficient	$\theta_{ikt}^{ \pm }$	Slack variable
α	α-cut level	$d_{kt} ,\beta_{kt}^{ - } ,\beta_{kt}^{ + }$	Triangular fuzzy numbers that is the fuzzy probability of occurrence