Abstract
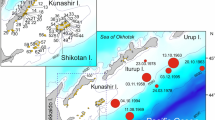
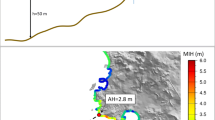
This study suggests the map representing the best-fit distribution of the tsunami run-up height time series. To obtain the map, the tsunami numerical simulations corresponding to the 11 different causative undersea earthquake were firstly performed. Then, the best-fit distribution representing the tsunami run-up height values for each modeling in-land grid point was determined using the probability plot correlation coefficient test. Then, the probability that the tsunami run-up height exceeding a 30 cm was estimated using the fitted distribution for each of the modeling grid point. Finally, the map of the best-fit distribution was produced based on the maximum exceedance probability out of the total 11 simulations. The log-normal distribution represents the distribution of the tsunami run-up heights for the wide area of the back of the quay while the normal distribution does the same along the coast line. The Gumbel and exponential distribution did not show a specific spatial pattern but were sparsely located. In addition, the map representing the probability that the tsunami run-up height exceeds a given criterion depth (30 cm) was created. We expect these two maps help the disaster managers and policy makers in making more precise decisions while placing and designing coastal structures by providing important information regarding the risk of the tsunami attack from statistical and temporal perspective.











Similar content being viewed by others
References
Blom G (1958) Statistical estimates and transformed beta-variables. Wiley, New York
Cho Y-S (1995) Numerical simulations of tsunami propagation and run-up. Ph.D. Thesis, Cornell University
Cho Y-S, Yoon SB (1998) A modified leap-frog scheme for linear shallow-water equations. Coast Eng J 40(2):191–205
Cho Y-S, Sohn D-H, Lee S-O (2007) Practical modified scheme of linear shallow-water equations for distant propagation of tsunamis. Ocean Eng 34(11–12):1769–1777
Choi BH, Ko JS, Chung HF, Kim EB, Oh IS, Choi JI, Sim JS, Pelinovsky E (1994) Tsunami runup survey at east coast of Korea due to the 1993 southwest of the Hokkaido earthquake. J Korean Soc Coast Ocean Eng 6(1):117–125
Choi BH, Pelinovsky E, Ryabov I, Hong SJ (2002) Distribution functions of tsunami wave heights. Nat Hazards 25(1):1–21
Chowdhury JU, Stedinger JR, Lu L-H (1991) Goodness-of-fit tests for regional generalized extreme value flood distributions. Water Resour Res 27(7):1765–1776
Cunnane C (1978) Unbiased plotting positions—a review. J Hydrol 37(3–4):205–222
Filliben JJ (1975) The probability plot correlation coefficient test for normality. Technometrics 17(1):111–117
Go ChN (1987) Statistical properties of tsunami runup heights at the coast of Kuril Island and Japan. Institute of Marine Geology and Geophysics, Sakhalin
Go ChN (1997) Statistical distribution of the tsunami heights along the coast, Tsunami and accompanied phenomena. Institute of Marine Geology and Geophysics, Sakhalin, pp 73–79
Google Earth (2012) Satellite Image Provided by Google Earth. (Accessed July 13, 2012)
Gringorten II (1963) A plotting rule for extreme probability paper. J Geophys Res 68(3):813–814
Heo J-H, Kho YW, Shin H, Kim S, Kim T (2008) Regression equations of probability plot correlation coefficient test statistics from several probability distributions. J Hydrol 355(1–4):1–15
Imamura F, Shuto N and Goto C (1988) Numerical simulations of the transoceanic propagation of tsunamis. Proceedings of 6th Congress Asian and Pacific Regional Division, IAHR, Japan, pp 265–272
Kajiura K (1983) Some statistics related to observed tsunami heights along the coast of Japan. In: Iida K, Iwasaki T (eds) Tsunamis: their science and engineering. Terra Scientific, Tokyo, pp 131–145
Korea Meteorological Administration (2012) Tsunami Events Database. http://www.kma.go.kr/weather/earthquake/tidalwave_03.jsp. Accessed 29 August 2012
Korean Peninsula Energy Development Organization (1999) Estimation of Tsunami Height for KEDO LWR Project. Korea Power Engineering Company Inc., Korea
Liu PLF, Cho Y-S, Yoon SB, Seo SN (1994) Tsunami: progress in prediction, disaster prevention and warning. In: EI-Sabh MI (ed) Numerical simulations of the 1960 Chilean tsunami propagation and inundation at Hilo. Hawaii. Kluwer Academic Publishers, Dordrecht, pp 99–115
Mansinha L, Smylie DE (1971) The displacement fields of inclined faults. Bull Seismol Soc Am 61(5):1433–1440
National Oceanic and Atmospheric Administration (2012) Tsunami Event Database. http://www.ngdc.noaa.gov/hazard/hazards.shtml. Accessed 13 July 2012
Pelinovsky E and Ryabov I (1999) Statistics of along-shore distribution of tsunami waves, applied problems of mathematics and informatics, Nizhny Novgorod: Technical University, pp 50–69
Pelinovsky E, Yuliadi D, Prasetya G, Hidayat R (1997a) The 1996 Sulawesi tsunami. Nat Hazards 16(1):29–38
Pelinovsky E, Yuliadi D, Prasetya G, Hidayat R (1997b) The January 1, 1996 Sulawesi Island tsunami. Int J Tsunami Soc 15(2):107–123
Shin H, Jung Y, Jeong C, Heo J (2012) Assessment of modified Anderson–Darling test statistics for the generalized extreme value and generalized logistic distributions. Stoch Environ Res Risk Assess 26:105–114
Sohn D-H, Ha T, Cho Y-S (2009) Distant tsunami simulation with corrected dispersion effects. Coast Eng J 51(2):123–141
USGS (2012) Earthquake Hazards Program, Japan, Seismicity Map—1900 to Present, http://earthquake.usgs.gov/earthquakes/world/japan/seismicity.php
Van Dorn WG (1965) Tsunamis. In: Chow VT (ed) Advances in hydroscience. Academic Press, London, pp 1–48
Vogel RM (1986) The probability plot correlation coefficient test for the normal, lognormal, and Gumbel distributional hypotheses. Water Resour Res 22(4):587–590
Vogel RM, Kroll CN (1989) Low-flow frequency-analysis using probability-plot correlation coefficients. J Water Resour Plan Manag 115(3):338–357
Vogel RW, McMartin DE (1991) Probability plot goodness-of-fit and skewness estimation procedures for the Pearson type-3 distribution. Water Resour Res 27(12):3149–3158
Yoon SB (2002) Propagation of tsunamis over slowly varying topography. J Geophys Res 107(10): 4(1)–4(11)
Acknowledgments
This research was supported by a grant [NEMA-ETH-2012-5] from the Earthquake and Tsunami Hazard Mitigation Research Group, National Emergency Management Agency of Korea.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cho, YS., Kim, Y.C. & Kim, D. On the spatial pattern of the distribution of the tsunami run-up heights. Stoch Environ Res Risk Assess 27, 1333–1346 (2013). https://doi.org/10.1007/s00477-012-0669-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-012-0669-7