1 Introduction

Artificial neural networks (ANN) techniques have been successfully applied across a broad spectrum of problem domains such as pattern recognition and regression, since their renaissance in the mid-1980s. Most ANN applications in engineering mainly fall in the category of prediction, in which an unknown relationship exists between a set of input factors and an output (Sudheer 2005). The objective of these studies is to find a formula between the selected input variables and the output based on a representative set of historic examples. The formula is then extended to predict the outcome of any given input. The computational efficiency of ANNs has provided many promising results in the field of hydrology and water resources engineering. This interest has been motivated by the complex nature of hydrological systems and the ability of ANNs to model nonlinear relationships (Maier et al. 2010).

Despite the large number of applications, ANNs still remain something of a numerical enigma. Apart from the major criticism that ANNs lack transparency (Abrahart et al. 2010), many researchers mention that ANN development is stochastic in nature, and no identical results can be reproduced on different occasions (Elshorbagy et al. 2010a, b). This is a significant weakness, and it is hard to trust the reliability of networks addressing real-world problems without the ability to produce comprehensible decisions. Therefore, a significant research effort is needed to address this deficiency of ANNs (Maier et al. 2010). In fact, there is a belief that ANN point predictions are of limited value where there is uncertainty in the data or variability in the underlying system.

Statistically, the ANN output approximates the average of the underlying target conditioned on the NN input vector (Bishop 1995). However, ANN predictions convey no information about the sampling errors and the prediction accuracy. The limited acceptance of the ANN model applications can be plausibly attributed to the difficulty observed in assigning confidence interval (or prediction interval) to the output (Shrestha and Solomatine 2006), which might improve the reliability and credibility of the predictions.

In the literature, several methods have been proposed for construction of prediction intervals and assessment of the ANN output uncertainty (Khosravi et al. 2010; Sonmez 2011). While they differ in the way of implementation, the methodology of all of them are common: train an ANN through minimization of an error based function, such as sum of squared errors, and then construct the prediction interval for the ANN outputs. The delta technique introduced by Chryssolouris et al. (1996) considers linearising the ANN model around a set of parameters, and constructing the prediction interval by application of standard asymptotic theory to the linearized model. However this method is based on the assumption that noise is homogenous and normally distributed which may not be true in many real world problems (Ding and He 2003). The Bayesian technique is another method for construction of prediction intervals (MacKay 1992). Despite the strength of the supporting theories, the method suffers from massive computational burden, and requires calculation of the Hessian matrix of the cost function for construction of prediction intervals (Papadopoulos et al. 2001). A mean–variance estimation-based method for prediction interval construction has also been proposed by Nix and Weigend (1994). The method uses an ANN to estimate the characteristics of the conditional target distribution. Additive Gaussian noise with non constant variance is the key assumption of the method for predictive interval construction. However, this method underestimates the variance of data, leading to a low empirical coverage probability, as discussed in Ding and He (2003). Bootstrap is one of the most frequently used techniques in the literature for construction of prediction intervals for ANN forecasts (Srivastav et al. 2007). The main advantage of this method is its simplicity and ease of implementation. It does not require calculation of complex derivatives and the Hessian matrix involved in the delta and Bayesian techniques.

The challenge for performing an uncertainty analysis of ANN outputs lies in the fact that the ANNs have large degrees of freedom in their development. Consequently, the hydrologic applications have received little attention in assessing the uncertainty in ANN model predictions, with the exception of a few. Probably the first attempt was by Dawson et al. (2000) who reported a six member ensemble mean of radial basis function neural network. The ensembles were created by varying the internal transfer function, and the corresponding variation in model output was considered as a measure of uncertainty. Ensemble modeling approach was also explored by Boucher et al. (2010). Firat and Gungor (2010) identified the best ANN model structures by constructing various input structures. Kingston et al. (2005) applied Bayesian training method to assess the parametric uncertainty of ANN models, and found that the Bayesian approach produces prediction limits that indicate the level of uncertainty in the predictions. Further the comparison of their results with deterministic ANN show that Bayesian training of neural network not only improves the quality of prediction, the prediction interval from the Bayesian network helps when forecasts were made outside the range of the calibration data. Khan and Coulibaly (2006) defined the posterior distribution of network weights through a Gaussian prior distribution and a Gaussian noise model. Their results indicated the predictive distribution of the network outputs by integrating over the posterior distribution with the assumption that posterior of network weights is approximated to Gaussian during prediction. Srivastav et al. (2007) quantified parameter uncertainty through bootstrapping of input examples. The model structure was assumed to be deterministic. Sharma and Tiwari (2009) and Tiwari and Chatterjee (2010) used a similar approach to quantify the variability in ANN predictions to estimate prediction intervals. Han and Kwong (2007) proposed a method to understand the uncertainty in ANN hydrologic models with the heuristic that the distance between the input vector at prediction and all the training data provide a valuable indication on how well the prediction would be. However, their method did not quantify the uncertainty of the model parameters or the predictions. In case of structural uncertainty, Zhang et al. (2009) applied Bayesian Neural Network (BNN) to predict the uncertainty and their results shows that BNN based models give reasonable estimate of uncertainty in stream flow simulation. Shrestha and Nestmann (2009) investigated the uncertainty in the case of a stage-discharge relationship by defining fuzzy uncertainty bounds for the relationship curve. Alvisi and Franchini (2011) considered the ANN parameters as fuzzy numbers, and estimated the prediction intervals of stream flow predictions.

This paper presents a method that combines the bootstrap technique with the first order uncertainty analysis (FOUA) method to evaluate the parametric and predictive uncertainty associated with the ANN models applied to rainfall–runoff modeling. The earlier studies that used bootstrap techniques did not consider developing the uncertainty bounds of the predictions; rather most of them reported the simulated variability in predictions. While FOUA can be easily implemented without any computational burden, the practical implementation of the FOUA method hinges on the calculation of sensitivity coefficients that are the first order partial derivative of the model output with respect to model parameters involved in modeling. If the model under consideration is complex or non analytical (such as ANN), the applications becomes challenging, and this may be the plausible reason for it to receive little attention by the ANN hydrologic community.

The sections that follow are organized in the following way. Following this introduction, the theoretical considerations of FOUA in ANN models is described. Then, the methodology proposed for uncertainty analysis in this work is presented, and is demonstrated through a case study. The results are analyzed, and compared with the results of bootstrap method in detail in the succeeding sections. The article ends with the conclusions drawn from the presented case study.

2 Methodology

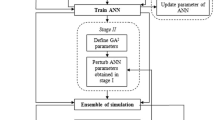
An ANN attempts to mimic, in a very simplified way, the human mental and neural structure and functions (Hsieh 1993). It can be characterized as massively parallel interconnections of simple neurons that function as a collective system. The multi layer perceptron (MLP) is the most popular ANN architecture in use today (Dawson and Wilby 1998; Aksoy and Dahamsheh 2009; Maier et al. 2010). It assumes that the unknown function (between input and output) is represented by a multi layer, feed forward network of sigmoid units. More details about the functioning of ANN are available in various literatures and are not presented herein for brevity. The parameters of the ANN are generally obtained using an optimization algorithm, and genetic algorithm (Holland 1975; Goldberg 1989; Behzadian and Kapelan 2009) is employed in the current study.

The methodology envisaged in this study for quantifying the uncertainty of ANN output involves the calculation of sensitivity coefficients that are the first order partial derivative of the model output with respect to model parameters involved in modelling, estimation of statistical moments of the parameters, and thereby developing the uncertainty bands. The following sections details these three steps in the uncertainty evaluation.

2.1 First derivative of ANN model

The proposed methodology is explained with generalized neural network structure as shown in Fig. 1 with n input neurons (x 1,…,x n ), h hidden neurons (z 1,…,z h ), and m output neurons (y 1,…,y m ). Let i, j, and k be the indices (number of neurons) representing input, hidden, and output layers, respectively. Let τ j be the bias for neuron z j and φ k be the bias for neuron y k . Let w ij be the weight of the connection from neuron x i to neuron z j and β jk the weight of connection from neuron z j to y k .

Fig. 1
figure 1

Structure of generalized neural network

Full size image

The model output (y p ) is the function of inputs, weights and biases as shown in Eq. (1).

$$ y_{p} = f(x_{np} ,w_{ij} ,\beta_{jk} ,\tau_{j} ,\varphi_{k} ), $$
(1)

where y p is the model output of any pattern (p = 1, 2, 3,…, total number of pattern), x np is the model input of any pattern (p = 1, 2, 3,…, total number of pattern, where suffix n represents number of input variables).

The Taylor series expansion of the above model can be written as the following form,

$$ y_{p} = \overline{y} + \sum\limits_{r = 1}^{\infty } {\left( {\frac{{\partial^{r} y_{p} }}{{\partial w_{1}^{r} }}} \right)} \left( {\frac{{w_{1} - \overline{{w_{1} }} }}{r!}} \right) + \cdots \sum\limits_{r = 1}^{\infty } {\left( {\frac{{\partial^{r} y_{p} }}{{\partial w_{k}^{r} }}} \right)} \left( {\frac{{w_{k} - \overline{{w_{k} }} }}{r!}} \right) + \cdots , $$
(2)

where k is the total number of parameter and r is the order of partial derivative of the parameter.

The above generalized Taylor series expansion is approximated to first derivative for the weight vectors w ij , β jk and bias vectors τ j , φ k as given in Eq. (3).

$$ y_{p} = \overline{y} + \frac{{\delta y_{p} }}{{\delta w_{ij} }}\left( {\frac{{w_{ij} - \overline{{w_{ij} }} }}{1!}} \right) + \frac{{\delta y_{p} }}{{\delta \beta_{jk} }}\left( {\frac{{\beta_{jk} - \overline{{\beta_{jk} }} }}{1!}} \right) + \frac{{\delta y_{p} }}{{\delta \tau_{j} }}\left( {\frac{{\tau_{j} - \overline{{\tau_{j} }} }}{1!}} \right) + \frac{{\delta y_{p} }}{{\delta \varphi_{k} }}\left( {\frac{{\varphi_{k} - \overline{{\varphi_{k} }} }}{1!}} \right) $$
(3)

in which \( \overline{y} = f(\overline{x} );\,\frac{{\delta y_{p} }}{{\delta w_{ij} }},\frac{{\delta y_{p} }}{{\delta \beta_{jk} }},\frac{{\delta y_{p} }}{{\delta \tau_{j} }},\frac{{\delta y_{p} }}{{\delta \varphi_{k} }} \) are called the 1st-order sensitivity coefficient indicating the rate of change of the function output with respect to its weight vectors and bias values. Hence, the variance of output of the neural network model with respect to its weights and biases is written as,

$$ \left( {\sigma_{{y_{p} }} } \right)^{2} = \left( {\frac{{\delta y_{p} }}{{\delta w_{ij} }}} \right)^{2} \left( {\sigma_{{w_{ij} }} } \right)^{2} + \left( {\frac{{\delta y_{p} }}{{\delta \beta_{jk} }}} \right)^{2} \left( {\sigma_{{\beta_{jk} }} } \right)^{2} + \left( {\frac{{\delta y_{p} }}{{\delta \tau_{j} }}} \right)^{2} \left( {\sigma_{{\tau_{j} }} } \right)^{2} + \left( {\frac{{\delta y_{p} }}{{\delta \varphi_{k} }}} \right)^{2} \left( {\sigma_{{\varphi_{k} }} } \right)^{2} $$
(4)

The equation for the neural network with i—input, j—hidden and k—output node can be written as follows,

$$ y_{p} = \frac{1}{{1 + e^{{ - \beta_{jk} \; \times \;\left[ {\frac{1}{{1 + S^{ - 1} }}} \right] - \varphi_{k} }} }} $$
(5)

The first derivative of weights and bias vectors are derived as,

$$ \frac{{\delta y_{p} }}{{\delta w_{ij} }} = \frac{{\beta_{jk} \; \times \;x_{np} }}{{\left\{ {S\; \times \;e^{{\left[ {\frac{{\beta_{jk} }}{{1 + S^{ - 1} }} + \phi_{k} } \right]}} \; \times \;(1 + S^{ - 1} )^{2} \; \times \;\left[ {1 + e^{{ - \phi_{k} - \frac{\beta }{{1 + S^{ - 1} }}}} } \right]^{2} } \right\}}} $$
(6)
$$ \frac{{\delta y_{p} }}{{\delta \beta_{jk} }} = \left| {e^{{\frac{{\beta_{jk} }}{{1 + S^{ - 1} }} + \phi_{k} }} \; \times \;(1 + S^{ - 1} )\; \times \;\left[ {1 + e^{{\frac{{ - \beta_{jk} }}{{1 + S^{ - 1} }} - \phi_{k} }} } \right]^{2} } \right|^{ - 1} $$
(7)
$$ \frac{{\delta y_{p} }}{{\delta \tau_{j} }} = \frac{{\beta_{jk} }}{{\left\{ {S\; \times \;e^{{\left[ {\frac{{\beta_{jk} }}{{1 + S^{ - 1} }} + \phi_{k} } \right]}} \; \times \;(1 + S^{ - 1} )^{2} \; \times \;\left[ {1 + e^{{ - \phi_{k} - \frac{\beta }{{1 + S^{ - 1} }}}} } \right]^{2} } \right\}}} $$
(8)
$$ \frac{{\delta y_{p} }}{{\delta \phi_{k} }} = \left| {e^{{\frac{{\beta_{jk} }}{{1 + S^{ - 1} }} + \phi_{k} }} \; \times \;\left[ {1 + e^{{\frac{{ - \beta_{jk} }}{{1 + S^{ - 1} }} - \phi_{k} }} } \right]^{2} } \right|^{ - 1} $$
(9)

where,

$$ S = e^{{\tau_{j} + w_{ij} \times x_{np} }} ,\,\quad S^{ - 1} = e^{{ - \tau_{j} - w_{ij} \times x_{np} }} $$

Equations (4)–(9) can be used to estimate the uncertainty of ANN output y p .

2.2 Statistical moments of ANN parameters

The mean and standard deviation of the ANN parameters is obtained using the method proposed by Srivastav et al. (2007) that used Bootstrap technique. In their method, the total example set is divided into two sets: training and validation sets. The validation set is kept aside, and random bootstrapping with replacement is performed on the training set in order to evaluate the parametric variation with varying training sets. The ANN model is trained on the bootstrapped training set (BTS) with fixed initial weights; the remaining patterns in the training set apart from BTS are employed for cross validation. After one such model is trained, another training set is drawn from the pool using bootstrapping, and the network is trained on the new BTS using the same initial weights used earlier. A sufficiently large number of networks are trained using this procedure (500 in the current study). All the networks so developed are evaluated on the validation set kept aside by computing various performance indices. The variation in the weights of the network and the output of the network over the whole trained network is a measure of the uncertainty in the model parameters and predictions, respectively that are obtained through sampling the training dataset. The properties of the probability distribution of ANN parameters can be obtained from the variability of the parameters of the trained networks (Srivastav et al. 2007).

2.3 Predictive uncertainty

The variability in the parameters of ANN, as mentioned earlier, can be obtained from the bootstrap techniques. The statistical properties of the parameter variation, which is a measure of the uncertainty, can be employed for estimating the standard error of estimate of the predictions, and their corresponding confidence band. The estimated uncertainty interval is expected to contain specified portion of observation from the validation period data set. It is to be noted that the parametric uncertainty is considered to be the major source of uncertainty through which the predictive uncertainty is quantified.

3 Study area and Data used

The proposed method for estimation of uncertainty in ANN model predictions is demonstrated through the case study of Upper White watershed from the USA. An index map of the watersheds is presented in Fig. 2. Upper White River Watershed is located in central Indiana, with a catchment area of 2,950 km². Daily rainfall and runoff data during the period (01–01–1999–19–02–2008) from USGS gauging station 03351000 is used for analysis. In which the calibration and validation data set is separated as (01–01–1999–06–11–2005) and (07–11–2005–19–02–2008) respectively. The statistics of rainfall and discharge is presented in Table 1, for selected period to develop the model. The main stream in this watershed is White river. The basin receives an average annual precipitation of 1,041 mm. The mean elevation of this watershed is 236.73 m. The land use in the watershed is predominantly agricultural (46 %), followed by forest (9 %), pasture/hay (30 %), water/wetland (1 %) and urban area (14 %) respectively. The average slope of this watershed is 16 %. An ANN model for computing the daily runoff from this basin using the rainfall information is developed and assessed for the uncertainty in model predictions as discussed in the following sections.

Fig. 2
figure 2

An index map of Upper White River watershed

Full size image
Table 1 Statistics of data used for model development
Full size table

4 ANN model development

One of the most important steps in the ANN hydrologic model development process is the determination of significant input variables (Bowden et al. 2004a, b). Generally some degree of a priori knowledge is used to specify the initial set of candidate inputs (e.g. Campolo et al. 1999; Thirumalaiah and Deo 2000). However, the relationship between the variables is not clearly known a priori, and hence often an analytical technique, such as cross-correlation, is employed (e.g. Sajikumar and Thandaveswara 1999; Luk et al. 2000; Silverman and Dracup 2000; Sudheer et al. 2002). The major disadvantage associated with using cross-correlation is that it is only able to detect linear dependence between two variables, while the modeled relationship may be highly nonlinear. Nonetheless, the cross-correlation methods represent the most popular analytical techniques for selecting appropriate inputs (Bowden et al. 2004a, b).

The current study employed a statistical approach suggested by Sudheer et al. (2002) to identify the appropriate input vector. The method is based on the heuristic that the potential influencing variables corresponding to different time lags can be identified through statistical analysis of the data series that uses cross-, auto-, and partial auto correlations between the variables in question. Using this procedure, the identified most influencing variables for the Upper White watershed is Rt−2, Rt−1, Rt, Qt−2 and Qt−1 as shown in Fig. 3, in which, Rt and Qt corresponds to the rainfall and flow at time t, and the suffix (t−1) and (t−2) represented the time lagged values of the variable.

Fig. 3
figure 3

ANN model structure used in this study

Full size image

The number of hidden neurons in the network, which is responsible for capturing the dynamic and complex relationship between various input and output variables, was identified by various trials. The trial and error procedure started with two hidden neurons initially, and the number of hidden neurons was increased up to 10 with a step size of 1 in each trial.

A sigmoid function is used as the activation function in the hidden layer as well in output layer. As the sigmoid function has been used in the model, the input–output variables have been scaled appropriately to fall within the function limits using the range of the data. The training of the ANN was done using genetic algorithm as mentioned earlier. For each set of hidden neurons, the network was trained in batch mode (offline learning) to minimize the mean square error at the output layer. In order to check any over-fitting during training, a cross validation was performed by keeping track of the efficiency of the fitted model. The training was stopped when there was no significant improvement in the model efficiency, and the model was then tested for its generalization properties. The parsimonious structure that resulted in minimum error and maximum efficiency during training as well as validation was selected as the final form of the ANN model.

5 Results and discussion

5.1 Models’ performance

As mentioned earlier, this study used genetic algorithm to train the neural network in which the input–output patterns are sampled randomly using bootstrap method with replacement. A total number of 3,335 patterns were available for model development, which was divided into two sets: 2,500 patterns for training and the remaining (835) for validation. The validation data sets were corresponding to a continuous hydrograph. While bootstrapping, 2,000 samples were sampled from the training patterns, and the balance 500 were used for verifying the training especially to check any over fitting. During this exercise, a total of 500 models were created, and the summary statistics of the performance, in terms of Nash–Sutcliffe efficiency (Nash and Sutcliffe 1970), of these models are presented in Table 2. The mean value of NSE in calibration phase is comparable with that in the validation phase. The standard deviation of NSE indicates that the variation of model’s prediction is within a range of ±4.2 and ±6.6 % during calibration and validation stage respectively which according to Srivastav et al. (2007) is very satisfactory. The large range between minimum and maximum value of NSE indicates that the sampled input patterns have an impact on model performance, which in turn illustrates the uncertainty associated with the training samples. The statistics show that the variation of performance across the models is not very significant, as the standard deviation of efficiency is very less. The number of bootstrapped samples (500 in this study) was arrived at after trial and error, and it was found that 500 models is a good representation for further analysis.

Table 2 Nash Sutcliff efficiency statistics for 500 models
Full size table

5.2 Parametric uncertainty

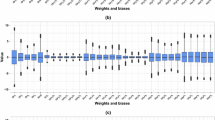
The final architecture of the ANN model developed for Upper White watershed was 5–3–1 (Fig. 3). Consequently, the model has a total of 22 parameters that includes the weights and biases. The variability of these parameters across the ensemble models (500 bootstrapped models) were characterized by developing their probability distribution using Easyfit software (Schittkowski 2002). The χ2-statistic was used to identify the best representing distribution. The results are presented in Table 3, and it can be observed that the distribution of these parameters is different from each other. It was observed that most of the parameters follow beta distribution, with varying scale and position characteristics, plausibly due to the property of the distribution that it can be rescaled and shifted to create distributions with a wide range of shapes over any finite range. It is to be noted that all the output connection weights and the weights connecting the inputs Q t−1 follow beta distribution, with comparable values of distribution characteristics. This plausibly indicates that the contribution of these weights to the final output may be similar. It is observed that all the bias connection follow log normal distribution. The role of bias connections is to counter balance the effects of weights in activation function. Lognormal distributions often provide a good representation for a physical quantity that extends from zero to + infinity and is positively skewed. In addition, it can include any order of magnitude of variance. This could be the reason that they follow lognormal distribution. The weights connecting rainfall inputs follow different distributions that include gamma and normal distribution, and indicate that the importance of parallel computing performed in ANN. The information obtained about the probability distribution is very much useful in fixing the prior distribution of parameters in the analysis.

Table 3 Probability distribution function statistics of 500 models
Full size table

On an average, the connection weight values range between −7.5 and 7.5 and it has a mean closely zero for all the parameters. The weights connecting the rainfall information has tighter distribution than weights connecting the flow values. The reason for such behavior may be the flow values largely distributed and hence the corresponding weights require larger domain of values (−10 to 10) in training of neural networks. In addition, it is to be noted that most influencing input variables produces larger variance distribution of parameters and hence discharge influences more than rainfall in prediction and similar observation is reported (Srivastav et al. 2007). It is also observed that there is no strong correlation existing between the parameters, except few. All the weights connecting the input Q t−1 to hidden nodes are strongly correlated with the weights connecting the hidden to output nodes and average correlation values obtained was 0.89 and all these connection weights follow same distributional (beta distribution).

5.3 Uncertainty band of prediction

The predictive uncertainty associated with the ANN outputs is derived using the FOUA. In addition to estimating the standard error of estimate, the 95 % uncertainty interval is computed using the standard error. Two quantitative measures are used for analyzing the level of uncertainty in this study: (i) percentage of coverage (POC) and (ii) average width (AW) (Shrestha and Solomatine 2006; Zhang et al. 2009). The POC assesses the number of observed values that falls within the prediction band. A value of 100 % for POC indicates that the entire observed values are included in the prediction band. While AW gives the AW of the prediction band, and narrow band is preferable over a large band. The 95 % uncertainty interval computed using FOUA method is presented in Figs. 4 and 5 respectively for calibration and validation data period. It may be noted that a period from 12 January 1999 to 12 April 1999 (calibration period) is presented in Fig. 4 for brevity. While it is evident from Figs. 4 and 5 that the uncertainty interval contains most of the observed values, it is observed that the observed values are falling more close to the upper bound of the uncertainty interval. This is a major concern, as it leads to questioning the performance of ANN models. It is to be noted that the maximum performance obtained for the 500 ensembles of ANN models was only 88 % efficiency (Table 2), and it illustrates the concern observed from Figs. 4 and 5. It is also observed that the peak discharge is not appropriately modeled by any of the 500 ensembles, which reiterate the general concern (Sudheer et al. 2002; Srivastav et al. 2007) about the ANN. This could be plausibly attributed to less number of patterns on peak flow range for ANN to adequately get trained.

Fig. 4
figure 4

The 95 % modeling uncertainty intervals of stream flow during calibration period (FOUA)

Full size image
Fig. 5
figure 5

The 95 % modeling uncertainty intervals of stream flow during validation period (FOUA)

Full size image

In order to assess the predictive uncertainty in different ranges of flow, the available data was grouped into three ranges following Nayak et al. (2005). The POC and AW statistics for different ranges of flow, and the entire data set together are presented in Table 4. It can be seen that during the calibration period the POC value was 48.78 % for the total data sets. A value of POC equal to 53/60 % was observed during validation, which shows that the method is consistent and produces fairly equal level of quantification without any bias. The AW value was lower in calibration (24.21 m3/s) compared to that in validation (30.96 m3/s). Considering different ranges of flow, it is observed that 74 % of flow data in calibration and validation period fall in low flow category. It was 22 and 4 % respectively for medium and high flow category. This reinforces the reasons discussed earlier for a lower performance of ANN on peak flows. It is noted from Table 4 that the POC in different ranges of flow was comparable across calibration and validation. It is observed that the AW statistic varies in different ranges of flow (varying from 16.25 m3/s in low flow range to 56.49 and 130.61 m3/s in medium and high flow ranges respectively).

Table 4 Quantitative estimation of 95 % uncertainty interval
Full size table

It is to be noted that the FOUA method majorly depends on the mean and standard deviation of the parameters, and the estimate of first derivatives. Therefore, the band of uncertainty depends on the accuracy of these characteristics. In this study, it is observed that the weights connecting the hidden nodes to output node, and the weights connecting the input node Q t−1 to the hidden nodes have relatively large variance, and therefore can be considered as more influencing the prediction band compared to other parameters.

5.4 Comparison between FOUA and bootstrap method

In order to evaluate the effectiveness of the proposed uncertainty analysis method, the results of the method have been compared with another method, bootstrap method. The bootstrap method is selected here for comparison since this method is simple to evaluate, and is also reported to be computationally simpler compared to other methods. Table 4 contains the uncertainty interval in terms of the POC and AW for the bootstrap method. It is evident from table that the FOUA method proposed in this study provides a better estimate of the prediction band as is evidenced by the relatively high value of POC and AW in all ranges of flow. The prediction band derived from bootstrap method is presented in Figs. 6 and 7 for the calibration and validation period (same as that for FOUA in Figs. 4 and 5). It can be observed that the bootstrap method (Figs. 6, 7) provide a narrow band for prediction making most of the measured values to fall outside the band. A plausible reason for this could be that the bootstrap method is non parametric, and therefore the uncertainty which is quantified directly from the simulations may not be capturing the parametric uncertainty appropriately. On the other hand, FOUA being an analytic method produces better estimate of uncertainty since it is derived using the variability of parameters as well first order partial derivative of each parameter in the developed model. Nonetheless, there could be several factors which pose difference in uncertainty estimation between methods, and the major reason could probably be that our understanding of hydrologic uncertainty is still far from complete (Zhang et al. 2009). Further, it is worth mentioning that the proposed method is able to derive the predictive uncertainty band much better compared to simple bootstrap method, and is less complex compared to any other existing methods for deriving uncertainty band.

Fig. 6
figure 6

The 95 % modeling uncertainty intervals of stream flow during calibration period (bootstrap)

Full size image
Fig. 7
figure 7

The 95 % modeling uncertainty intervals of stream flow during validation period (bootstrap)

Full size image

6 Conclusions

The FOUA on ANN models is illustrated for a case study on river flow forecasting. This approach reduces the computational burden and time of simulation for uncertainty analysis with limited statistical parameters such as mean and variance of the neural network weight vectors and biases. The parameter variability was obtained by bootstrap technique with replacement on the available observed data. The estimated uncertainty was assessed through two quantitative measures viz. POC, AW. A comparison of these indices across calibration and validation phase suggested that the results are consistent. In addition, uncertainty evaluation is performed on different domains of flow such as low, medium and high (categorised based on their statistical characteristics) to assess if the uncertainty estimated are influenced by the magnitude of flow. It is observed that the quantified level of uncertainty is found to be varying with the magnitude of the flow and it is directly proportional. Further the uncertainty band derived using the FOUA method is compared with that derived using the bootstrap method. The comparison was performed by using two indices POC and AW. Considering these two measures simultaneously, the FOUA method quantifies the predictive uncertainty better than the bootstrap method.