Planning of municipal solid waste management systems under dual uncertainties: a hybrid interval stochastic programming approach

Abstract

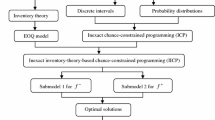
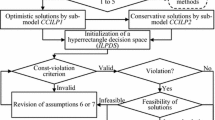
In this study, a random-boundary-interval linear programming (RBILP) method is developed and applied to the planning of municipal solid waste (MSW) management under dual uncertainties. In the RBILP model, uncertain inputs presented as interval numbers can be directly communicated into the optimization process; besides, intervals with uncertain lower and upper bounds can be handled through introducing the concept of random boundary interval. Consequently, robustness of the optimization process can be enhanced. To handle uncertainties with such complex presentations, an integrated chance-constrained programming and interval-parameter linear programming approach (ICCP) is proposed. ICCP can help analyze the reliability of satisfying (or risk of violating) system constraints under uncertainty. The applicability of the proposed RBILP and ICCP approach is validated through a case study of MSW management. Violations for capacity constraints are allowed under a range of significant levels. Interval solutions associated with different risk levels of constraint violation are obtained. They can be used for generating decision alternatives and thus helping waste managers to identify desired policies under various environmental, economic, and system-reliability constraints.

Appendix: Definitions regarding interval numbers

Definition A1

Let x denotes a closed set of real numbers. An interval number x ^± is defined as an interval with known upper and lower bounds but unknown distribution information for x. That is x ^± = [x ⁻, x ⁺] = {t∈x|x ⁻  ≤ t ≤ x ⁺}, where x ⁻ and x ⁺ are the lower and upper bounds of x ^±, respectively. When x ⁻  = x ⁺, x ^± becomes a deterministic number.

Definition A2

For x ^±, the following relationships holds: x ^± ≥ 0, iff x ⁻  ≥ 0 and x ⁺≥0; x ^± ≤ 0, iff x ⁻  ≤ 0 and x ⁺≤0.

Definition A3

For x ^± and y ^±, the order relations are as follows: x ^± ≥ y ^±, iff x ⁻ ≥ y ⁻ and x ⁺ ≥ y ⁺; x ^± = y ^±, iff x ⁻ = y ⁻ and x ⁺ = y ⁺; x ^± > y ^±, iff x ^± ≥ y ^± and x ^± ≠ y ^±.

Definition A4

For x ^±, Sign(x ^± ) is defined as ${\text{Sign}}(x^{ \pm } ) = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if}}\,x^{ + } \ge 0} \\ { - 1} & {{\text{if}}\,x^{ + }\,<\,0} \\ \end{array} } \right..$

Definition A5

For x ^±, its absolute value |x|^± is defined as $\left| x \right|^{ \pm } = \left\{ {\begin{array}{*{20}c} {x^{ \pm } } & {{\text{if}}\,x^{ \pm } \ge 0} \\ { - x^{ \pm } } & {{\text{if}}\,x^{ \pm }\,<\,0} \\ \end{array} } \right..$ Thus, we have $\left| x \right|^{ - } = \left\{ {\begin{array}{*{20}c} {x^{ - } } & {{\text{if}}\,x^{ \pm } \ge 0} \\ { - x^{ + } } & {{\text{if}}\,x^{ \pm }\,<\,0} \\ \end{array} } \right.$ and $\left| x \right|^{ + } = \left\{ {\begin{array}{*{20}c} {x^{ + } } & {{\text{if}}\,x^{ \pm } \ge 0} \\ { - x^{ - } } & {{\text{if}}\,x^{ \pm }\,<\,0} \\ \end{array} } \right..$

Definition A6

Let R ^± denote a set of interval numbers. An interval vector X ^± is a tupel of interval numbers, and an interval matrix Y ^± is a matrix whose elements are interval numbers: X ^± = {x _i ^± = x ⁻ _i , x ⁺ _i ] | for any i} ∈ {R ^±}^1 × n, Y ^± = {y ^± _ij  = [y ⁻ _ij , y ⁺ _ij ] | for any i, j} ∈ {R ^±}^m×n.

Definition A7

In this paper, for interval vectors or matrices: X ^± ≥/≤ 0 iff x ^± _ij  ≥/≤ 0 for any i and j, where X ^± ∈ {R ^±}^m × n(m ≥ 1, and m = integer).

Definition A8

Let * ∈ {+ , −, × , ÷} be a binary operation on interval numbers. For x ^± and y ^±: x ^± * y ^±  = [min (x * y), max (x * y)], x ⁻  ≤ x ≤ x ⁺, y ⁻  ≤ y ≤ y ⁺. In the case of division, it is assumed that y ^± does not contain zero. Hence x ^± + y ^±= [ x ⁻ + y ⁻, x ⁺ + y ⁺]; x ^± − y ^± = [ x ⁻ − y ⁺, x ⁺ − y ⁻]; x ^± ×  y ^±  = [min (x × y), max (x × y)], x ⁻  ≤ x ≤ x ⁺, y ⁻  ≤ y ≤ y ⁺; x ^± ÷ y ^±  = [min (x÷y), max (x÷y)], x ⁻  ≤ x ≤ x ⁺, y ⁻  ≤ y ≤ y ⁺.