Skip to main content
SpringerLink
Log in

Risk assessment for optimal freshwater inflow in response to sustainability indicators in semi-arid coastal bay

  • Original Paper
  • Published:
Stochastic Environmental Research and Risk Assessment Aims and scope Submit manuscript

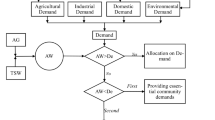
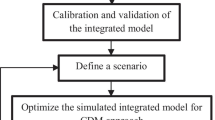
Abstract

Coastal zones are the primary interface for the exchange of natural and man-made materials between terrestrial and coastal ecosystems. While continuous industrial development and population growth in the coastal region promote unprecedented economic prosperity, water resource management in bay and estuary areas turns out to be a crucial challenge. Therefore, local, state, and federal water planning groups are attempting to manage the supply of freshwater inflow based on sustainability goals, especially for semi-arid coastal regions like South Texas. Surface and ground water management practices in this semi-arid coastal region are implemented to ensure an ever-lasting water supply on one hand and to maintain ecosystem integrity in the bay and estuary system on the other hand. The aim of this study is to apply a stochastic compromise programming model to identify a compromise solution under uncertainty in terms of two competing objectives: minimizing freshwater release from a coastal reservoir and maximizing fishery harvest in its associated bay—Corpus Christi Bay, South Texas. The global criterion method used in the solution procedure seeks to select a compromise solution that possesses the shortest distance from a positive ideal solution (PIS) and the farthest distance from a negative ideal solution (NIS). Solutions were found using three distance-based functions in conjunction with stochastic constraints reflecting the risk levels involved in decision-making. Results indicate that current flows in the mouth of the Nueces River are not sufficient to maintain the salinity level and to satisfy harvest requirements in the Corpus Christi Bay if water supply goal in the city has higher priority. Therefore, a sustainable management plan of exploring the structure of demand and supply is highly desirable in this fast growing urban region.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Abbreviations

Q j :

The inflow for jth month (j = 1, ..., 12) (106 m3/month)

QLB j and QUB j :

The lower and upper bounds for jth month (j = 1, ..., 12) (106 m3/month)

H k :

The harvest of kth species (k = 1,..., l) (103 kg/year)

H ratio :

The harvest ratio (unitless)

TH:

The total anticipated annual harvest (103 kg/year)

S ij :

The salinity at location i for month j (ppt)

SLB ij :

The lower bound for the salinity at location i for month j (ppt)

SUB ij :

The upper bound for the salinity at location i for month j (ppt)

AS ij :

The antecedent salinity of preceding month (ppt)

a i , b i and c i :

The regression constants (unitless)

P :

The probability (%)

S ijavg :

The salinity mean value at each location i (ppt)

α:

The predetermined confidence level (unitless)

B s :

The bimonthly inflow (106 m3/bimonth)

s :

An index for seasons (unitless)

a k , b ks , c ks , d ks and e ks :

The regression constants for kth species and sth season (unitless)

x * :

The ideal solution

F(x*):

The ideal objective vector

d PIS :

The PIS distance

d NIS :

The NIS distance

r :

An integer valued exponent (unitless)

d i :

The random variable

Q p :

The sum of inflows for a 2-month period (p=SO for September–October, ND for November–December, JF for January–February, MA for March–April, MJ for May–June, and JA for July–August) (106 m3/bimonth)

PIS:

Positive ideal solution

NIS:

Negative ideal solution

TWDB:

Texas Water Development Board

TCEQ:

Texas Commission for Environmental Protection

TPWD:

Texas Parks and Wildlife Department

TxBLEND:

Texas Estuarine Blend Model

TxEMP:

Texas water development board Estuarine Mathematical Programming Model

SLB:

Salinity lower bound

SUB:

Salinity upper bound

MOP:

Multiobjective optimization problems

SCP:

Stochastic compromise programming

CCP:

Chance constrained programming

VMP:

Vector maximum problem

USGS:

United Sates Geological Survey

TxRR:

Texas rainfall-runoff model

USDOI:

United States Department of Interior

USDOC:

United States Department of Commerce

CPUE:

Catch per unit effort

References

  • Bao YX (1992) Methodology for determining the optimal freshwater inflows into bays and estuaries. PhD Dissertation, Department of Civil Engineering, The University of Texas at Austin

  • Bao YX, Mays LW (1994) Optimization of freshwater inflows to Lavaca-Tres Palacious, Texas Estuary. J Water Resour Plan Manag ASCE 102(2):218–236

    Google Scholar 

  • Bao YX, Tung YK, Mays LW, Ward GH Jr (1989) Analysis of effect of freshwater inflows on estuary fishery resources, Report to the Texas Water Development Board by The Center for Research in Water Resources, The University of Texas at Austin, Austin, Texas. Technical Memorandum 89(2):49

    Google Scholar 

  • Bellman RE (1957) Dynamic programming. Princeton University Press, Princeton

    Google Scholar 

  • Bellman R, Dreyfus SE (1962) Applied dynamic programming. Princeton University Press, Princeton

    Google Scholar 

  • Bender M, Simonovic SP (2000) A fuzzy compromise approach to water resource systems planning under uncertainty. Fuzzy Sets Syst 115:35–44

    Google Scholar 

  • Boychuk LM, Ovchinnikov VO (1973) Principal methods for solution of multicriterial optimization problems (survey). Soviet Automat Control 6(3):1–4

    Google Scholar 

  • Braga BPF Jr, Yeh WW-G, Becker L, Barros MTL (1991) Stochastic optimization of multiple-reservoir-system operation. J Water Resour Plan Manag 117(4):471–481

    Google Scholar 

  • Charnes A, Cooper WW (1959) Chance-constrained programming. Manag Sci 6:73–79

    Google Scholar 

  • Curry GL, Helm JC, Clark RA (1973) Chance-constrained model of system of reservoirs. J Hydraul Div ASCE 99(HY12):2353

    Google Scholar 

  • Eisel LM (1970) Comments on the linear decision rule in reservoir management and design by C. S. ReVelle, E. Joeres, W. Kirby. Water Resour Res 6(4):1239–1241

    Google Scholar 

  • Ellis JH (1990) Integrating multiple long-range transport models into optimization methodologies for acid rain policy analysis. Eur J Operat Res 46:313–321

    Google Scholar 

  • Ellis JH, McBean EA, Farquhar GJ (1985) Chance-constrained/stochastic linear programming model for acid rain abatement—I. Complete collinearity and noncollinearity. Atmos Environ 19(6):925–937

    Google Scholar 

  • Fults DM, Logan GR, Hancock LF (1976) A practical monthly optimum operations model. J Water Resour Plan Manag Div 102(1):63–76

    Google Scholar 

  • Goicoechea A, Hansen DR, Duckstein L (1982) Multiobjective decision analysis with engineering and business applications. Wiley, New York

    Google Scholar 

  • Gupta AK, Sivakumar AI (2002) Simulation based multiobjective schedule optimation in semiconductor manufacturing. In: Yucesan E, Chen CH, Snowdon JL, Charnes JM (eds) Proceedings of the 2002 winter simulation conference, pp 1862–1870

  • Heidari M, Chow VT, Kokotovic PV, Meredith DD (1971) Discrete differential dynamic programming approach to water resources systems optimization. Water Resour Res 7(2):273–282

    Google Scholar 

  • Huang WC, Harboe R, Bogardi JJ (1991) Testing stochastic dynamic programming models conditioned on observed or forecasted inflows. J Water Resour Plan Manag 117(1):28–36

    Google Scholar 

  • Huang WC, Yuan LC, Lee CM (2002) Linking genetic algorithms with stochastic dynamic programming to the long-term operation of a multireservoir system. Water Resour Res 38(12):1304–1313

    Google Scholar 

  • Huntley D, Leeks G, Walling D (2001) Land–Ocean interaction: managing and modelling fluxes from river basins to coastal seas. International Water Association Publication, London

    Google Scholar 

  • Hwang CL, Masud ASM (1979) Multiple objective decision making: method and application. Springer, Berlin Heidelberg New York

    Google Scholar 

  • Hwang CL, Yoon KS (1981) Multiple attribute decision making: method and application. Springer, Berlin Heidelberg New York

    Google Scholar 

  • Hwang CL, Paidy SR, Yoon KS (1980) Mathematical programming with multiple objectives: a tutorial. Comput Operat Res 7:5–31

    Google Scholar 

  • Joeres EF, Liebman JC, ReVelle CS (1971) Operating rules for joint operation of raw water sources. Water Resour Res 7(2):225–235

    Google Scholar 

  • Johnson JE (1976) Status of endangered and threatened fish species in Colorado, Tech. Note 280, US Department of the Interior, Bureau of Land Management

  • Kelman J, Stedinger JR, Cooper LA, Hsu E, Yuan SQ (1990) Sampling stochastic dynamic programming applied to reservoir operation. Water Resour Res 26(3):447–454

    Google Scholar 

  • Kim YO, Palmer RN (1997) Value of seasonal flow forecasts in Bayesian stochastic programming. J Water Resour Plan Manag 123(6):327–335

    Google Scholar 

  • Liang Q, Johnson LE, Yu YS (1996) A comparison of two methods for multiobjective optimization for reservoir operation. J Amer Water Resour Assoc 32(2):333–340

    Google Scholar 

  • LINDO (2002) LINDO Systems Inc. http://www.lindo.org.

  • Liu B, Odanaka T (1999) Dynamic fuzzy criterion model for reservoir operations and a case study. Comput Math Appl 37(11–12):65–75

    Google Scholar 

  • Longley WL (ed) (1994) Freshwater inflows to Texas bays and estuaries: ecological relationships and methods for determination of needs. Texas Water Development Board and Texas Parks and Wildlife Department, Austin, p 386

    Google Scholar 

  • Loucks DP (1970) Some comments on linear decision rules and chance constraints. Water Resour Res 6(2):668–671

    Google Scholar 

  • Loucks DP, Stedinger JR, Haith DA (1981) Water resources systems planning and analysis. Prentice Hall, Englewood Cliffs

    Google Scholar 

  • Martin QW (1987) Estimating freshwater inflow needs for Texas estuaries by mathematical programming. Water Resour Res 23(2):230–238

    Google Scholar 

  • Matsumoto J (1992) User’s manual for the TWDB’s rainfall–runoff model. Texas Water Development Board, Austin

    Google Scholar 

  • Matsumoto J, Powell G, Brock D (1994) Freshwater-inflow need of estuary computed by Texas Estuarine MP model. J Water Resour Plan Manag ASCE 120(5):693–713

    Google Scholar 

  • Merino GG, Jones DD, Clements DL, Miller D (2003) Fuzzy compromise programming with precedence order in the criteria. Appl Math Comput 134(1):185–205

    Google Scholar 

  • Moncada E, Fontane DG, Gates TK (1994) Evaluating multi-purpose reservoir operations using fuzzy dynamic programming. In: Fontane DG, Tuvel HN (eds) Water policy and management: solving the problems. American Society of Civil Engineers, New York, pp 111–114

    Google Scholar 

  • Nandala KDW, Bogardi JJ (1995) Optimal operation of a reservoir for quality control using inflow and outflows. Water Sci Technol 31(8):273–280

    Google Scholar 

  • Nandalal KDW, Simonovic SP (2002) State-of-the-art report on system analysis methods for resolution of conflicts in water resources management. Division of Water Sciences, UNESCO

    Google Scholar 

  • Nayak SC, Arora SR (1971) Optimal capacities for a multireservoir system using the linear decision rule. Water Resour Res 7(3):485–498

    Google Scholar 

  • Ning X, Shi J, Liu Z, Cal Y (1996) Abundance and distribution of photosynthetic picocyanobacteria and picoeukaryotes in the Southern Ocean. Sci China C 26(2):164–171

    Google Scholar 

  • Powell GL, Matsumoto J, Brock D (2002) Methods for determining minimum freshwater inflow needs of Texas bays and estuaries. Estuary 25(68B):1262–1274

    Google Scholar 

  • Price JF (1979) On the scaling of stress-driven entrainment experiments. J Fluid Mech 90:509–529

    Google Scholar 

  • Price JF, Barringer MO (1994) Outflows and deep water production by marginal seas. Progr Oceanogr 33:161–200

    Google Scholar 

  • Prodanovic P, Simonovic SP (2002) Comparison of fuzzy set ranking methods for implementation in water resources decision making. Can J Civ Eng 29:692–701

    Google Scholar 

  • Pulich W, Tolan J, Lee WY, Alvis W (2002) Freshwater inflow recommendation for the Nueces estuary. Texas Parks and Wildlife Department and Texas Water Development Board, Austin

    Google Scholar 

  • ReVelle CS, Kirby W (1970) Linear decision rule in reservoir management and design, 2. Performance optimization. Water Resour Res 6(4):1033–1044

    Google Scholar 

  • ReVelle CS, Joeres E, Kirby W (1969) The linear decision rule in reservoir management and design, I. Development of stochastic model. Water Resour Res 5(4):767–777

    Google Scholar 

  • Saad M, Turgeon A, Bigras P, Duquette R (1994) Learning disaggregation technique for the operation of long-term hydroelectric power systems. Water Resour Res 30(11):3195–3202

    Google Scholar 

  • Salukvadze M (1974) On the existence of solutions in problems of optimization under vector valued criteria. J Opt Theory Appl 13(2):203–217

    Google Scholar 

  • Simonovic SP (1977) Stochastic model of a multipurpose reservoirs with chance constraints. Trans Inst Jaroslvav Cerni Eograd 59(5)

  • Simonovic SP (1979) Two-step algorithm for design-stage long-term control of a multipurpose reservoir. Adv Water Resour 2:47

    Google Scholar 

  • Tabucanon MT (1988) Multiple criteria decision making in industry. Elsevier, Amsterdam

    Google Scholar 

  • Tecle A (1992) Selecting a multicriterion decision making technique for watershed resources management. Water Resour Bull 28(1):129–140

    Google Scholar 

  • Teixeira ADS, Mariño MA (2002) Coupled reservoir operation-irrigation scheduling by dynamic programming. J Irrig Drain Eng 128(2):63–73

    Google Scholar 

  • Tejada-Guibert JA, Johnson SA, Stedinger JR (1993) Comparision of two approaches for implementing multireservoir policies derived using stochastic dynamic programming. Water Resour Res 29(12):3969–3980

    Google Scholar 

  • Tejada-Guibert JA, Johnson SA, Stedinger JR (1995) The value of hydrologic information in stochastic dynamic programming models of multireservoir system. Water Resour Res 31(10):2571–2579

    Google Scholar 

  • Texas Parks & Wildlife (2003) Exploring Texas—about Corpus Christi Bay. Available on-line http://www.tpwd.state.tx.us/

  • Texas Water Development Board (TWDB) (2003) Environmental water needs: planning criteria of the consensus state water plan. Austin Texas, USA

    Google Scholar 

  • Tilmant A., Duckstein L, Persoons E (2002a) Comparison of fuzzy and nonfuzzy optimal reservoir operating policies. J Water Resour Plan Manag 128(6):390–398

    Google Scholar 

  • Tilmant A, Faouzi EH, Vanclooster M (2002b) Optimal operation of multipurpose reservoirs using flexible stochastic dynamic programming. Appl Soft Comput 2(1F):61–74

    Google Scholar 

  • Tung YK, Bao YX, Mays LW, Ward WH (1990) Optimization of freshwater inflow to estuaries. J Water Resour Plan Manag ASCE 116(4):567–584

    Google Scholar 

  • Turgeon A (1981) Optimal operation of multireservoir power systems with stochastic inflows. Water Resour Res 16(2):275–283

    Google Scholar 

  • Turgeon A, Charbonneau R (1998) An aggregation-disaggregation approach to long-term reservoir management. Water Resour Res 34(12):3585–3594

    Google Scholar 

  • Wurbs RA (1993) Reservoir-system simulation and optimization models. J Water Resour Plan Manag 119(4):455–472

    Google Scholar 

  • Yakowitz S (1982) Dynamic programming applications in water resources. Water Resour Res 18(4):673–696

    Google Scholar 

  • Yeh WW-G (1985) Reservoir management and operation models: a state-of-art review. Water Resour Res 21(12):1797–1818

    Google Scholar 

  • Yu PL, Zeleny M (1975) The set of all non-dominated solutions in linear cases and a multicriteria simplex method. J Math Anal Appl 49(2):430–468

    Google Scholar 

  • Zeleny M (1973) Compromise programming. In: Cockrane J, Zeleny M (eds) Multiple criteria decision making. University of South Carolina Press, Columbia, pp 262–301

    Google Scholar 

  • Zeleny M (1974) A concept of compromise solutions and the method of the displaced ideal. Comput Operat Res 1(4):479–496

    Google Scholar 

  • Zeleny M (1982) Multiple criteria decision making. McGraw-Hill Book Company, New York

    Google Scholar 

Download references

Acknowledgements

The authors acknowledge the financial support of NSF grant (CREST Award No: 0206259) as well as the data reports cited and used in this analysis. The authors extend their deep gratitude to the various supports from Dr. Matsumoto J. and the Texas Water Development Board for sharing their invaluable information.

Author information

Authors and Affiliations

  1. Department of Environment Engineering, Texas A&M University-Kingsville, Kingsville, TX, USA

    Jae-Hyung Ji & Ni-Bin Chang

Authors
  1. Jae-Hyung Ji
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ni-Bin Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ni-Bin Chang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ji, JH., Chang, NB. Risk assessment for optimal freshwater inflow in response to sustainability indicators in semi-arid coastal bay. Stoch Environ Res Ris Assess 19, 111–124 (2005). https://doi.org/10.1007/s00477-004-0219-z

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00477-004-0219-z

Keywords

Search

Navigation