Abstract
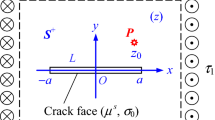
We present a boundary integral formulation for anisotropic interface crack problems based on an exact Green's function. The fundamental displacement and traction solutions needed for the boundary integral equations are obtained from the Green's function. The traction-free boundary conditions on the crack faces are satisfied exactly with the Green's function so no discretization of the crack surfaces is necessary. The analytic forms of the interface crack displacement and stress fields are contained in the exact Green's function thereby offering advantage over modeling strategies for the crack. The Green's function contains both the inverse square root and oscillatory singularities associated with the elastic, anisotropic interface crack problem. The integral equations for a boundary element analysis are presented and an example problem given for interface cracking in a copper-nickel bimaterial.
Similar content being viewed by others
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Berger, J., Tewary, V. Boundary integral equation formulation for Interface cracks in anisotropic materials. Computational Mechanics 20, 261–266 (1997). https://doi.org/10.1007/s004660050246
Issue Date:
DOI: https://doi.org/10.1007/s004660050246