Skip to main content
SpringerLink
Log in

A data-driven multi-flaw detection strategy based on deep learning and boundary element method

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

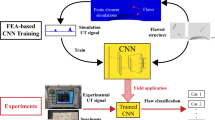
In this article, we propose a data-driven multi-flaw detection strategy based on deep learning and the boundary element method (BEM). In the training phase, BEM is implemented to generate the database, while the block LU decomposition technique is employed to reduce the computational cost. Then the Convolutional Neural Networks (CNNs) are adopted as a deep learning model to find the relationship between the input signals and the geometries of flaws through the training process. In the test phase, the performance of trained models will be evaluated with unseen data. As a typical inverse problem, the solution to a flaw detection problem is not always unique. In the present work, we demonstrate that such non-uniqueness is detrimental to the training process, and avoid them through some specific treatments. In order to enhance the robustness of the model, the idea of data augmentation is introduced to flaw detection tasks. The numerical results show that the presented model could produce accurate predictions in both single- and multi-flaw detection tasks with proper training. Additionally, data augmentation could significantly help against the noise.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28

Similar content being viewed by others

References

  1. Banerjee S, Leckey C (2020) Computational Nondestructive Evaluation Handbook: Ultrasound Modeling Techniques. CRC Press, Florida

    Book  Google Scholar 

  2. Hellier CJ (2013) Handbook of nondestructive evaluation. McGraw-Hill Education, New York

    Google Scholar 

  3. Aquino W, Bunting G, Miller ST, Walsh TF (2019) A gradient-based optimization approach for the detection of partially connected surfaces using vibration tests. Comput Methods Appl Mech Eng 345:323–335. https://doi.org/10.1016/j.cma.2018.11.002

    Article  MathSciNet  MATH  Google Scholar 

  4. Hematiyan MR, Khosravifard A, Shiah YC (2017) A new stable inverse method for identification of the elastic constants of a three-dimensional generally anisotropic solid. Int J Solids Struct 106–107:240–250. https://doi.org/10.1016/j.ijsolstr.2016.11.009

    Article  Google Scholar 

  5. Jung J, Taciroglu E (2014) Modeling and identification of an arbitrarily shaped scatterer using dynamic xfem with cubic splines. Comput Methods Appl Mech Eng 278:101–118. https://doi.org/10.1016/j.cma.2014.05.001

    Article  MathSciNet  MATH  Google Scholar 

  6. Kassab AJ, Moslehy FA, Daryapurkar AB (1994) Nondestructive detection of cavities by an inverse elastostatics boundary element method. Eng Anal Boundary Elem 13(1):45–55. https://doi.org/10.1016/0955-7997(94)90006-X

    Article  Google Scholar 

  7. Mallardo V, Aliabadi MH (1998) A BEM sensitivity and shape identification analysis for acoustic scattering in fluid–solid problems. Int J Numer Methods Eng 41(8):1527–1541. https://doi.org/10.1002/(SICI)1097-0207(19980430)41:8<1527::AID-NME352>3.0.CO;2-O

  8. Mellings SC, Aliabadi MH (1993) Dual boundary element formulation for inverse potential problems in crack identification. Eng Anal Boundary Elem 12(4):275–281. https://doi.org/10.1016/0955-7997(93)90054-O

    Article  Google Scholar 

  9. Nishimura N, Kobayashi S (1991) A boundary integral equation method for an inverse problem related to crack detection. Int J Numer Meth Eng 32(7):1371–1387. https://doi.org/10.1002/nme.1620320702

    Article  MATH  Google Scholar 

  10. Sun H, Waisman H, Betti R (2016) A sweeping window method for detection of flaws using an explicit dynamic xfem and absorbing boundary layers. Int J Numer Meth Eng 105(13):1014–1040. https://doi.org/10.1002/nme.5006

    Article  MathSciNet  Google Scholar 

  11. Zhang C, Nanthakumar SS, Lahmer T, Rabczuk T (2017) Multiple cracks identification for piezoelectric structures. Int J Fract 206(2):151–169. https://doi.org/10.1007/s10704-017-0206-2

    Article  Google Scholar 

  12. Boukellif R, Ricoeur A (2020) Identification of crack parameters and stress intensity factors in finite and semi-infinite plates solving inverse problems of linear elasticity. Acta Mech 231(2):795–813. https://doi.org/10.1007/s00707-019-02575-9

    Article  MathSciNet  MATH  Google Scholar 

  13. Eleni NC, Badri H, Haim W, Andrew WS (2011) Experimental application and enhancement of the xfem-ga algorithm for the detection of flaws in structures. Computers Struct 89(7):556–570. https://doi.org/10.1016/j.compstruc.2010.12.014

    Article  Google Scholar 

  14. Rabinovich D, Givoli D, Vigdergauz S (2007) Xfem-based crack detection scheme using a genetic algorithm. Int J Numer Meth Eng 71(9):1051–1080. https://doi.org/10.1002/nme.1975

    Article  MathSciNet  MATH  Google Scholar 

  15. Chengbin D, Wenhu Z, Shouyan J, Xiaodong D (2020) Dynamic xfem-based detection of multiple flaws using an improved artificial bee colony algorithm. Comput Methods Appl Mech Eng 365:112995. https://doi.org/10.1016/j.cma.2020.112995

    Article  MathSciNet  MATH  Google Scholar 

  16. Sun H, Waisman H, Betti R (2013) Nondestructive identification of multiple flaws using xfem and a topologically adapting artificial bee colony algorithm. Int J Numer Meth Eng 95(10):871–900. https://doi.org/10.1002/nme.4529

    Article  MathSciNet  MATH  Google Scholar 

  17. Zhao W, Du C, Jiang S (2018) An adaptive multiscale approach for identifying multiple flaws based on xfem and a discrete artificial fish swarm algorithm. Comput Methods Appl Mech Eng 339:341–357. https://doi.org/10.1016/j.cma.2018.04.037

    Article  MathSciNet  MATH  Google Scholar 

  18. Boukellif R, Ricoeur A (2014) Parameter identification for cracks in elastic plate structures based on remote strain fields. Int J Solids Struct 51(11):2123–2132. https://doi.org/10.1016/j.ijsolstr.2014.02.017

    Article  Google Scholar 

  19. Khodadad M, Dashti Ardakani M (2009) Application of the inverse elasticity problem to identify irregular interfacial configurations. Eng Anal Boundary Elem 33(6):872–879. https://doi.org/10.1016/j.enganabound.2008.10.012

    Article  MathSciNet  MATH  Google Scholar 

  20. Karniadakis GE, Kevrekidis IG, Lu L, Perdikaris P, Wang S, Yang L (2021) Physics-informed machine learning. Nat Rev Phys 3(6):422–440. https://doi.org/10.1038/s42254-021-00314-5

    Article  Google Scholar 

  21. Raissi M, Perdikaris P, Karniadakis GE (2019) Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys 378:686–707. https://doi.org/10.1016/j.jcp.2018.10.045

    Article  MathSciNet  MATH  Google Scholar 

  22. Samaniego E, Anitescu C, Goswami S, Nguyen-Thanh VM, Guo H, Hamdia K, Zhuang X, Rabczuk T (2020) An energy approach to the solution of partial differential equations in computational mechanics via machine learning: concepts, implementation and applications. Comput Methods Appl Mech Eng 362:112790. https://doi.org/10.1016/j.cma.2019.112790

    Article  MathSciNet  MATH  Google Scholar 

  23. Jagtap AD, Kharazmi E, Karniadakis GE (2020) Conservative physics-informed neural networks on discrete domains for conservation laws: applications to forward and inverse problems. Comput Methods Appl Mech Eng 365:113028. https://doi.org/10.1016/j.cma.2020.113028

    Article  MathSciNet  MATH  Google Scholar 

  24. Mishra S, Molinaro R (2021) Estimates on the generalization error of physics-informed neural networks for approximating a class of inverse problems for pdes. IMA J Numer Anal. https://doi.org/10.1093/imanum/drab032

    Article  MATH  Google Scholar 

  25. Liu SW, Huang JH, Sung JC, Lee CC (2002) Detection of cracks using neural networks and computational mechanics. Comput Methods Appl Mech Eng 191(25):2831–2845. https://doi.org/10.1016/S0045-7825(02)00221-9

    Article  MATH  Google Scholar 

  26. Zacharias J, Hartmann C, Delgado A (2004) Damage detection on crates of beverages by artificial neural networks trained with finite-element data. Comput Methods Appl Mech Eng 193(6):561–574. https://doi.org/10.1016/j.cma.2003.10.009

    Article  MATH  Google Scholar 

  27. Bigoni C, Hesthaven JS (2020) Simulation-based anomaly detection and damage localization: an application to structural health monitoring. Comput Methods Appl Mech Eng 363:112896. https://doi.org/10.1016/j.cma.2020.112896

    Article  MathSciNet  Google Scholar 

  28. Jiang S, Zhao L, Du C (2021) Combining dynamic xfem with machine learning for detection of multiple flaws. Int J Numer Methods Eng. https://doi.org/10.1002/nme.6791

    Article  MathSciNet  Google Scholar 

  29. Goodfellow I, Bengio Y, Courville A (2016) Deep learning. MIT press, Massachusetts

    MATH  Google Scholar 

  30. Krizhevsky A, Sutskever I, Hinton GE (2012) Imagenet classification with deep convolutional neural networks. Adv Neural Inf Process Syst 25:1097–1105

    Google Scholar 

  31. Khodabandehlou H, Pekcan G, Fadali MS (2018) Vibration-based structural condition assessment using convolution neural networks. Struct Control Health Monitor. https://doi.org/10.1002/stc.2308

    Article  Google Scholar 

  32. Liu T, Xu H, Ragulskis M, Cao M, Ostachowicz W (2020) A data-driven damage identification framework based on transmissibility function datasets and one-dimensional convolutional neural networks: verification on a structural health monitoring benchmark structure. Sensors 20(4):1059. https://doi.org/10.3390/s20041059

    Article  Google Scholar 

  33. Rus G, Lee S-Y, Gallego R (2005) Defect identification in laminated composite structures by bem from incomplete static data. Int J Solids Struct 42(5):1743–1758. https://doi.org/10.1016/j.ijsolstr.2004.07.028

    Article  MATH  Google Scholar 

  34. Ma C, Yu T, Van Lich L, Quoc Bui T (2017) An effective computational approach based on xfem and a novel three-step detection algorithm for multiple complex flaw clusters. Computers Struct 193:207–225. https://doi.org/10.1016/j.compstruc.2017.08.009

    Article  Google Scholar 

  35. Brebbia CA, Telles JCF, Wrobel LC (2012) Boundary element techniques: theory and applications in engineering. Springer, Berlin

    MATH  Google Scholar 

  36. Gallivan KA, Plemmons RJ, Sameh AH (1990) Parallel algorithms for dense linear algebra computations. SIAM Rev 32(1):54–135. https://doi.org/10.1137/1032002

    Article  MathSciNet  MATH  Google Scholar 

  37. He K, Zhang X, Ren S, Sun J (2015) Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In: 2015 IEEE International Conference on Computer Vision (ICCV), pp 1026–1034 IEEE Computer Society, Santiago, Chile. https://doi.org/10.1109/ICCV.2015.123 IEEE

  38. Rumelhart DE, Hinton GE, Williams RJ (1988) Learning internal representations by error propagation. In: Collins, A., Smith, E.E. (eds.) Readings in Cognitive Science, pp 399–421. Morgan Kaufmann, Massachusetts . https://doi.org/10.1016/B978-1-4832-1446-7.50035-2. https://www.sciencedirect.com/science/article/pii/B9781483214467500352

  39. Hinton G, Srivastava N, Swersky K (2012) Neural networks for machine learning lecture 6a overview of mini-batch gradient descent. Coursera, University of Toronto. Preprint at https://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf

  40. Kingma DP, Ba J (2015) Adam: a method for stochastic optimization. In: 3rd International Conference on Learning Representations, ICLR 2015 3rd International Conference on Learning Representations, ICLR 2015 http://arxiv.org/abs/1412.6980

  41. Ioffe S, Szegedy C (2015) Batch normalization: accelerating deep network training by reducing internal covariate shift. In: Proceedings of the 32nd International Conference on International Conference on Machine Learning - Vol 37, pp 448–456 PMLR

  42. Wang J, Perez L (2017) The effectiveness of data augmentation in image classification using deep learning. Convolut Neural Netw Vis Recognit 11:1–8

    Google Scholar 

  43. Gal Y, Ghahramani Z (2015) Bayesian convolutional neural networks with bernoulli approximate variational inference. CoRR abs/1506.02158 http://arxiv.org/abs/1506.02158

  44. Goodfellow IJ, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y (2014) Generative adversarial nets. In: Proceedings of the 27th International Conference on Neural Information Processing Systems - Vol 2 NIPS’14, pp 2672–2680 MIT Press, Cambridge, MA, USA

Download references

Acknowledgements

This study is supported by the projects from the National Natural Science Foundation of China, under Grant No.11672155 and No.12090030.

Author information

Authors and Affiliations

  1. Department of Engineering Mechanics, Tsinghua University, Beijing, 100089, China

    Jia Sun, Yinghua Liu, Zhenhan Yao & Xiaoping Zheng

Authors
  1. Jia Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yinghua Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhenhan Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiaoping Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaoping Zheng.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, J., Liu, Y., Yao, Z. et al. A data-driven multi-flaw detection strategy based on deep learning and boundary element method. Comput Mech 71, 517–542 (2023). https://doi.org/10.1007/s00466-022-02231-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-022-02231-5

Keywords

Search

Navigation