Abstract
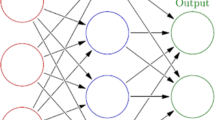
Artificial Neural Nets (ANN) have received huge attention in the scientific community over the last decade and are based on layered input-output type frameworks that are essentially adaptive nonlinear regressions of the form \({{{\mathcal {O}}}}={{{\mathcal {B}}}}({\varvec{I}},{\varvec{w}})\), where \({{{\mathcal {O}}}}\) is a desired output and \({{{\mathcal {B}}}}\) is the ANN comprised of (1) synapses, which multiply inputs (\(I_1, I_2, \ldots , I_M\)) by weights (\(w_1, w_2,\ldots , N\)) that represent the input relevance to the desired output, (2) neurons, which aggregate outputs from all incoming synapses and apply activation functions to process the data and (3) training, which calibrates the weights to match a desired overall output. A primary issue with ANN is the calibration of the synapse weights. This calibration can be cast as a nonconvex optimization problem, whereby the cost/error function represents the normed difference between observed data and the output of the ANN for a selected set of weights. The objective is to select a set of weight which minimizes the cost/error. One family of methods that are extremely well-suited for this process are genetic-based machine-learning algorithms. The goal of this short communication is to illustrate this process on a clear model problem.






Similar content being viewed by others
Notes
We also note that this algorithm is extremely easy to parallelize.
Note that no geometric or statistical information is required for the bounds.
References
Davis L (1991) Handbook of Genetic Algorithms. Thompson Computer Press
Ghosh S (2011) Micromechanical Analysis and Multi-Scale Modeling Using the Voronoi Cell Finite Element Method. CRC Press/Taylor & Francis
Ghosh S, Dimiduk D (2011) Computational Methods for Microstructure-Property Relations. Springer, NY
Gill P, Murray W, Wright M (1995) Practical optimization. Academic Press
Goldberg DE (1989) Genetic algorithms in search, optimization & machine learning. Addison-Wesley
Goldberg DE, Deb K (2000) Special issue on Genetic Algorithms. Computer Methods in Applied Mechanics & Engineering. 186(2–4):121–124
Hashin Z (1983) Analysis of composite materials: a survey. ASME Journal of Applied Mechanics. 50:481–505
Hashin Z, Shtrikman S (1962) On some variational principles in anisotropic and nonhomogeneous elasticity. J Mech Phys Solids 10:335–342
Hashin Z, Shtrikman S (1963) A variational approach to the theory of the elastic behaviour of multiphase materials. Journal of the Mechanics and Physics of Solids. 11:127–140
Holland JH (1975) Adaptation in natural & artificial systems. University of Michigan Press, Ann Arbor, Mich
Holland JH, Miller JH (1991) Artificial Adaptive Agents in Economic Theory (PDF). American Economic Review. 81 (2): 365-71. Archived from the original (PDF) on October 27, 2005
Jikov VV, Kozlov SM, Olenik OA (1994) Homogenization of differential operators and integral functionals. Springer-Verlag
Kachanov M, Tsukrov I, Shafiro B (1994) Effective moduli of solids with cavities of various shapes. Appl Mech Rev 47:S151–S174
Luenberger D (1974) Introduction to Linear & Nonlinear Programming. Addison-Wesley, Menlo Park
Maxwell JC (1867) On the dynamical theory of gases. Philos. Trans. Soc. London. 157:49
Maxwell JC (1873) A treatise on electricity and magnetism, 3rd edn. Clarendon Press, Oxford
Mura T (1993) Micromechanics of defects in solids, 2nd edn. Kluwer Academic Publishers
Onwubiko C (2000) Introduction to engineering design optimization. Prentice Hall
Rayleigh JW (1892) On the influence of obstacles arranged in rectangular order upon properties of a medium. Phil Mag 32:481–491
Torquato S (2002) Random Heterogeneous Materials: Microstructure & Macroscopic Properties. Springer-Verlag, New York
Zohdi TI (2018) Dynamic thermomechanical modeling and simulation of the design of rapid free-form 3D printing processes with evolutionary machine learning. Computer Methods in Applied Mechanics and Engineering Volume 331, 1 April 2018, Pages 343-362
Zohdi TI (2019) Electrodynamic machine-learning-enhanced fault-tolerance of robotic free-form printing of complex mixtures. Computational Mechanics. 63, pages 913-929 (2019)
Zohdi TI (2021) A Digital-Twin and Machine-learning Framework for the Design of Multiobjective Agrophotovoltaic Solar Farms. Comput Mech. https://doi.org/10.1007/s00466-021-02035-z
Zohdi TI (2021) A Digital-Twin and Machine-learning Framework for Ventilation System Optimization for Capturing Infectious Disease Respiratory Emissions. Archives of Computational Methods in Engineering. https://doi.org/10.1007/s11831-021-09609-3
Zohdi TI (2022) A digital-twin and machine-learning framework for precise heat and energy management of data-centers. Comput Mech. https://doi.org/10.1007/s00466-022-02152-3
Zohdi TI (2020) A machine-learning framework for rapid adaptive digital-twin based fire-propagation simulation in complex environments. Computer Methods Appl. Mech. Eng. 363:112907
Zohdi TI (2021) A digital twin framework for machine learning optimization of aerial fire fighting and pilot safety. Comput Methods Appl Mech Eng 373(1):113446
Zohdi TI, Wriggers P (2008) Introduction to computational micromechanics. Springer-Verlag
Zohdi TI, Monteiro PJM, Lamour V (2002) Extraction of elastic moduli from granular compacts. The International Journal of Fracture/Letters in Micromechanics. 115:L49–L54
Acknowledgements
This work has been partially supported by the UC Berkeley College of Engineering and the USDA AI Institute for Next Generation Food Systems (AIFS), USDA award number 2020-67021- 32855.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zohdi, T.I. A note on rapid genetic calibration of artificial neural networks. Comput Mech 70, 819–827 (2022). https://doi.org/10.1007/s00466-022-02216-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-022-02216-4