Phase field fracture in elasto-plastic solids: a length-scale insensitive model for quasi-brittle materials

Abstract

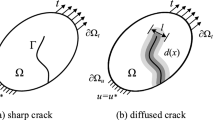
Phase-field methods for fracture have been integrated with plasticity for better describing constitutive behaviours. In most of the previous phase-field models, however, the length-scale parameter must be interpreted as a material property in order to match the material strength in experiments. This study presents a phase-field model for fracture coupled with plasticity for quasi-brittle materials with emphasis on insensitivity of the length-scale parameter. The proposed model is formulated using variational principles and implemented numerically in the finite element framework. The effective yield stress is calibrated to vary with the length-scale parameter such that the tensile strength remains the same. Moreover, semi-analytical solutions are derived to demonstrate that the length-scale parameter has a negligible effect on the stress–displacement curve. Five representative examples are considered here to validate the phase-field model for fracture in quasi-brittle materials. The simulated force–displacement curves and crack paths agree well with the corresponding experimental results. Importantly, it is found that the global structural response is insensitive to the length scale though it may influence the size of the failure zone. In most cases, a large length-scale parameter can be used for saving the computational cost by allowing the use of a coarse mesh. On the other hand, a sufficiently small length-scale parameter can be selected to prevent overly diffusive damage, making it possible for the proposed phase-field model to simulate the fracture behaviour with $\varGamma$-convergence.

Appendix A: Governing equations from the energetic principles and hybrid formulation

1.1 First-order stability condition

The energetic principles, namely stability condition, energy balance and irreversibility condition, are used to determine the state variables (${\mathbf{u}}, \lambda , d$). The first-order stability condition yields:

$$ \delta \varPi \ge 0,\quad \quad \quad \forall \left( {{\mathbf{u}}, \lambda , d} \right)\,{\text{admissible}} $$

(A1)

Use of the definition of the total energy in Eq. (8) leads to

$$ \begin{aligned} \delta \varPi & = \mathop \int\nolimits_{\Omega }^{{}} \left( {\left[ { - 2\left( {1 - d} \right)\left( {\frac{1}{2} {\varvec{\upvarepsilon}}^{\text{e}} :{\varvec{\upsigma}}_{0} + \sigma_{y0} \lambda } \right)\delta d + \frac{{g_{f} }}{{l_{c} }}\left( {l_{c}^{2} \nabla d \cdot \nabla \delta d + d \delta d} \right)} \right]} \right. \\ & \left. {\quad +\,\left( {1 - d} \right)^{2} {\varvec{\upsigma}}_{0} :\delta {\varvec{\upvarepsilon}} + \left( {1 - d} \right)^{2} \left( { - {\varvec{\upsigma}}_{0} :\frac{{{\text{d}}{\varvec{\upvarepsilon}}^{\text{p}} }}{{{\text{d}}\lambda }} + \sigma_{y0} } \right)\delta \lambda } \right){\text{d}}\varOmega - \mathop \int\nolimits_{\varOmega }^{{}} {\mathbf{b}} \cdot \delta {\mathbf{u}} {\text{d}}\varOmega - \mathop \int\nolimits_{\partial \varOmega }^{{}} {\mathbf{t}} \cdot \delta {\mathbf{u}} {\text{d}}\partial \varOmega \\ & \ge 0 \\ \end{aligned} $$

(A2)

I. Equilibrium equation.

For $\delta d = 0$ and $\delta \lambda = 0$, Eq. (A2) gives

$$ \mathop \int\nolimits_{\Omega }^{{}} {\varvec{\upsigma}}:\delta {\varvec{\upvarepsilon}}{\text{d}}\varOmega - \mathop \int\nolimits_{\varOmega }^{{}} {\mathbf{b}} \cdot \delta {\mathbf{u}} {\text{d}}\varOmega - \mathop \int\nolimits_{\partial \varOmega }^{{}} {\mathbf{t}} \cdot \delta {\mathbf{u}} {\text{d}}\partial \varOmega = 0 $$

(A3)

This is the weak form of the equilibrium equation. Integrating the first term of (A3) by parts gives

$$ \mathop \int\nolimits_{\Omega }^{{}} \left( {{\text{div}}{\varvec{\upsigma}} - {\mathbf{b}}} \right) \cdot \delta {\mathbf{u}}{\text{d}}\varOmega + \mathop \int\nolimits_{\partial \varOmega }^{{}} \left( {{\mathbf{n}} \cdot {\varvec{\upsigma}} - {\mathbf{t}}} \right) \cdot \delta {\mathbf{u}} {\text{d}}\partial \varOmega = 0 $$

(A4)

where ${\mathbf{n}}$ is the outward normal to the boundary $\partial \varOmega$. Then, the following local equilibrium equation can be obtained:

$$ {\text{div}}{\varvec{\upsigma}} + {\mathbf{b}} = 0 \quad {\text{in }}\varOmega $$

(A5a)

$$ {\mathbf{n}} \cdot {\varvec{\upsigma}} = {\mathbf{t}} \;{\text{on}} \;\partial \varOmega^{\text{s}} $$

(A5b)

along with the Dirichlet boundary condition:

$$ {\mathbf{u}} = {\tilde{\mathbf{u}}}\quad {\text{on}} \;\partial \varOmega^{\text{h}} $$

(A5c)

II. Damage yield criteria.

For $\delta {\mathbf{u}} = 0$ and $\delta \lambda = 0$, Eq. (A2) leads to

$$ \mathop \int\nolimits_{\Omega }^{{}} \left[ { - 2\left( {1 - d} \right)\left( {\frac{1}{2} {\varvec{\upvarepsilon}}^{\text{e}} :{\varvec{\upsigma}}_{0} + \sigma_{y0} \lambda } \right)\delta d + \frac{{g_{f} }}{{l_{c} }}\left( {l_{c}^{2} \nabla d \cdot \nabla \delta d + d \delta d} \right)} \right]{\text{d}}\varOmega \ge 0 $$

(A6)

which is the weak form of the damage criterion.

Then, Eq. (A6) gives

$$ f^{d} \left( {{\mathbf{u}}, \lambda , d} \right) \le 0\quad {\text{in}} \;\varOmega $$

(A7a)

$$ {\mathbf{n}} \cdot \nabla d \ge 0\quad {\text{on}} \;\partial \varOmega $$

(A7b)

with $f^{d} \left( {{\mathbf{u}},\lambda ,d} \right)$ being the damage yield surface defined as:

$$ f^{d} \left( {{\mathbf{u}},\lambda ,d} \right)\text{ := }2\left( {1 - d} \right)\left( {\frac{1}{2}{\varvec{\upvarepsilon}}^{\text{e}} :{\varvec{\upsigma}}_{0} + \sigma_{y0} \lambda } \right) + \frac{{g_{f} }}{{l_{c} }}\left( {l_{c}^{2} \Delta d - d} \right) $$

(A7c)

III. Plasticity yield criteria.

For $\delta {\mathbf{u}} = 0$ and $\delta d = 0$, Eq. (A2) leads to

$$ \mathop \int\nolimits_{\Omega }^{{}} \left[ {\left( {1 - d} \right)^{2} \left( { - {\varvec{\upsigma}}_{0} :\frac{{{\text{d}}{\varvec{\upvarepsilon}}^{\text{p}} }}{{{\text{d}}\lambda }} + \sigma_{y0} } \right)\delta \lambda } \right]{\text{d}}\varOmega \ge 0 $$

(A8)

which gives

$$ f^{p} ({\mathbf{u}}, \lambda , d )\le 0\quad {\text{in}} \;\varOmega $$

(A9a)

with $f^{p} ({\mathbf{u}}, \lambda , d)$ being the plasticity yield surface defined as

$$ f^{p} ({\mathbf{u}}, \lambda , d )\text{ := }\left( {1 - d} \right)^{2} \left[ {\sigma_{0}^{\text{eq}} \left( {{\mathbf{u}}, \lambda } \right) - \sigma_{y0} } \right] $$

(A9b)

where $\sigma_{0}^{\text{eq}}$ is the effective (undamaged) equivalent stress,

$$ \sigma_{0}^{\text{eq}} \left( {{\mathbf{u}}, \lambda } \right)\text{ := }{\varvec{\upsigma}}_{0} :\frac{{{\text{d}}{\varvec{\upvarepsilon}}^{\text{p}} }}{{{\text{d}}\lambda }} $$

(A9c)

The effective (undamaged) plasticity yield criterion can then be formulated as,

$$ f_{0}^{p} ({\mathbf{u}}, \lambda )\text{ := } \sigma_{0}^{\text{eq}} \left( {{\mathbf{u}}, \lambda } \right) - \sigma_{y0} $$

(A9d)

Thus,

$$ \frac{{{\text{d}}{\varvec{\upvarepsilon}}^{\text{p}} }}{{{\text{d}}\lambda }} = \frac{{{\text{d}}\sigma_{0}^{\text{eq}} }}{{{\text{d}}{\varvec{\upsigma}}_{0} }} = \frac{{\partial f_{0}^{p} }}{{\partial {\varvec{\upsigma}}_{0} }} = \frac{{\partial f^{p} }}{{\partial {\varvec{\upsigma}}}}\quad \Rightarrow {\text{d}}{\varvec{\upvarepsilon}}^{\text{p}} = {\text{d}}\lambda {\mathbf{a}} $$

(A9e)

where ${\mathbf{a}} = \frac{{\partial f^{p} }}{{\partial {\varvec{\upsigma}}}} = \frac{{\partial f_{0}^{p} }}{{\partial {\varvec{\upsigma}}_{0} }}$ stands for the normal direction of the plasticity yield function. Note that Eq. (A9e) is consistent with the associated plasticity. From Eq. (A9e), the evolution of the plastic strain does not depend on the phase-field damage, enabling a straightforward use of classical elasto-plastic algorithms.

1.2 Consistency conditions from energy balance principle

The energy balance principle states that the time derivative of the total energy should be zero, i.e., $\dot{\varPi } = 0.$ Hence,

$$ \begin{aligned} \dot{\varPi } & = \mathop \int\nolimits_{\Omega }^{{}} - f^{d} ({\mathbf{u}}, \lambda , d ) \dot{d} + \left( {{\text{div}}{\varvec{\upsigma}} - \varvec{b}} \right) \cdot {\dot{\mathbf{u}}} - f^{p} ({\mathbf{u}}, \lambda , d )\dot{\lambda }{\text{d}}\varOmega + \mathop \int\nolimits_{\partial \varOmega }^{{}} \left( {{\mathbf{n}} \cdot {\varvec{\upsigma}} - {\mathbf{t}}} \right) \cdot {\dot{\mathbf{u}}} {\text{d}}\partial \varOmega \\ & \quad + g_{f} l_{c} \mathop \int\nolimits_{\partial \varOmega }^{{}} {\mathbf{n}} \cdot \nabla d\dot{d} {\text{d}}\partial \varOmega = 0 \\ \end{aligned} $$

(A10)

Combination of Eqs. (A5a) and (A5b) and Eq. (A10) yields

$$ \dot{\varPi } = \mathop \int\nolimits_{\Omega }^{{}} - f^{d} ({\mathbf{u}}, \lambda , d ) \dot{d}{\text{d}}\varOmega + \mathop \int\nolimits_{\Omega }^{{}} - f^{p} ({\mathbf{u}}, \lambda , d )\dot{\lambda }{\text{d}}\varOmega + g_{f} l_{c} \mathop \int\nolimits_{\partial \varOmega }^{{}} {\mathbf{n}} \cdot \nabla d\dot{d} {\text{d}}\partial \varOmega = 0 $$

(A11)

Taking advantage of the irreversibility conditions together with Eqs. (A7a), (A7b) and (A9a), each term in Eq. (A11) should be equal to 0. Thus, the consistency conditions can be derived:

$$ f^{p} ({\mathbf{u}}, \lambda , d )\dot{\lambda } = 0\quad {\text{in }}\varOmega $$

(A12a)

$$ f^{d} ({\mathbf{u}}, \lambda , d ) \dot{d} = 0\quad {\text{in }}\varOmega $$

(A12b)

$$ {\mathbf{n}} \cdot \nabla d\dot{d} = 0\quad {\text{on}}\,\partial \varOmega $$

(A12c)

1.3 Clausius–Duhem dissipation inequality

The dissipated power $\dot{D}$ is required to have a non-negative value:

$$ \begin{aligned} \dot{D} = \mathop \int\nolimits_{\Omega }^{{}} \dot{\varphi }{\text{d}}\varOmega & = \mathop \int\nolimits_{\Omega }^{{}} \left( { - 2\left( {1 - d} \right)\sigma_{y0} \lambda - \frac{{g_{f} }}{{l_{c} }}\left( {l_{c}^{2} \Delta d - d} \right)} \right)\dot{d}{\text{d}}\varOmega \\ & \quad + \mathop \int\nolimits_{\Omega }^{{}} \left( {1 - d} \right)^{2} \sigma_{y0} \dot{\lambda }{\text{d}}\varOmega + \mathop \int\nolimits_{\partial \varOmega }^{{}} g_{f} l_{c} {\mathbf{n}} \cdot \nabla d\dot{d} {\text{d}}\partial \varOmega \ge 0 \\ \end{aligned} $$

(A13)

in which the first integral is positive since $\dot{d} \ge 0$ and $- 2\left( {1 - d} \right)\sigma_{y0} \lambda - \frac{{g_{f} }}{{l_{c} }}\left( {l_{c}^{2} \Delta d - d} \right) = - f^{d} \left( {{\mathbf{u}}, \lambda , d} \right) + \left( {1 - d} \right) {\varvec{\upvarepsilon}}^{\text{e}} :{\varvec{\upsigma}}_{0} \ge 0$; the second integral is positive simply because $\sigma_{y0} > 0$ and $\dot{\lambda } \ge 0$; and the last integral is equal to 0 directly from Eq. (A12c). Thus, the constitutive model of the elastoplastic-phase-field damage problem is thermodynamically admissible.

1.4 Alternative handling of phase-field equations and hybrid formulation

The variational inequality of Eq. (A6) accounts for the unilateral effect of the damage irreversibility. Here, if we first neglect the damage irreversibility, Eq. (A6) becomes

$$ \mathop \int\nolimits_{\Omega }^{{}} \left[ { - 2\left( {1 - d} \right)\left( {\frac{1}{2} {\varvec{\upvarepsilon}}^{\text{e}} :{\varvec{\upsigma}}_{0} + \sigma_{y0} \lambda } \right) \delta d + \frac{{g_{f} }}{{l_{c} }}\left( {l_{c}^{2} \nabla d \cdot \delta \nabla d + d \delta d} \right)} \right]{\text{d}}\varOmega = 0 $$

(A14)

The irreversibility of crack growth is then enforced by introducing a history functional ${\mathcal{H}}$:

$$ {\mathcal{H}}\text{ := }\mathop {\hbox{max} }\limits_{{\tau \in \left[ {0,t} \right]}} \left( {\frac{1}{2}{\varvec{\upvarepsilon}}^{\text{e}} :{\varvec{\upsigma}}_{0} } \right) + \sigma_{y0} \lambda $$

(A15)

Furthermore, in order to consider anisotropic damage, only the tensile part of elastic energy density is allowed to drive the evolution of the crack field [16]. Hence, the following history functional ${\mathcal{H}}^{ + }$ is used to replace ${\mathcal{H}}$:

$$ {\mathcal{H}}^{ + } \text{ := }\mathop {\hbox{max} }\limits_{{\tau \in \left[ {0,t} \right]}} \left\{ {\frac{\lambda }{2}{\text{tr}}\left( {{\varvec{\upvarepsilon}}^{\text{e}} } \right)_{ + }^{2} + \mu {\text{tr}}\left[ {\left( {{\varvec{\upvarepsilon}}_{ + }^{\text{e}} } \right)^{2} } \right]} \right\} + \sigma_{y0} \lambda $$

(A16)

where $x_{ + } : = \frac{{\left( {x + \left| x \right|} \right)}}{2}$ and ${\varvec{\upvarepsilon}}_{ + }^{\text{e}}$ is the positive part of ${\varvec{\upvarepsilon}}^{\text{e}}$. $\lambda$ and $\mu$ are the Lame constants. Thus, the weak form of the governing equation (A6) can be rewritten as:

$$ \mathop \int\nolimits_{\Omega }^{{}} \left[ { - 2\left( {1 - d} \right){\mathcal{H}}^{ + } \delta d + \frac{{g_{f} }}{{l_{c} }}\left( {l_{c}^{2} \nabla d \cdot \delta \nabla d + d \delta d} \right)} \right]{\text{d}}\varOmega = 0 $$

(A17)

which leads to the strong form:

$$ - 2\left( {1 - d} \right){\mathcal{H}}^{ + } + \frac{{g_{f} }}{{l_{c} }}\left( { - l_{c}^{2} \Delta d + d} \right) = 0\quad {\text{in }}\varOmega $$

(A18a)

$$ {\mathbf{n}} \cdot \nabla d = 0\quad {\text{on }}\partial \varOmega $$

(A18b)

Note that the elastic energy density is only decomposed in the phase-field problem but not in the displacement field problem. In other words, the degradation function is applied to the whole elastic energy density in the definition of the nominal stress in Eq. (5). As a result, a linear momentum balance equation can remain within a staggered scheme, and thus the computational efficiency can be significantly improved, though the rigorous variational consistency of the problem could be somewhat lost. This is the so-called hybrid formulation for phase-field fracture and interested readers can refer to Ambati et al. [89] for more details.