A meshless method for the nonlinear von Kármán plate with multiple folds of complex shape

Abstract

We present a meshless discretisation method for the solution of the non-linear equations of the von Kármán plate containing folds. The plate has Mindlin–Reissner kinematics where the rotations are independent of the derivatives of the normal deflection, hence discretised with different shape functions. While in cracks displacements are discontinuous, in folds, rotations are discontinuous. To introduce a discontinuity in the rotations, we use an enriched weight function previously derived by the authors for cracks (Barbieri et al. in Int J Numer Methods Eng 90(2):177–195, 2012). With this approach, there is no need to introduce additional degrees of freedom for the folds, nor the mesh needs to follow the folding lines. Instead, the folds can be arbitrarily oriented and have endpoints either on the boundary or internal to the plate. Also, the geometry of the folds can be straight or have kinks. The results show that the method can reproduce the sharp edges of the folding lines, for various folding configurations and compare satisfactorily with analytical formulas for buckling or load-displacement curves from reference solutions.

1 Introduction

Folded structures are omnipresent in various fields of science and engineering. For example, they manifest as chevron and detachment folds in geology [1,2,3], origami mechanisms in mechanical engineering [4], origami mechanical metamaterials [5], roofs in civil engineering [6], and even in the arts [7] and architecture [8, 9].

A vast literature exists on origami and folded structures, and a thorough review would be outside the bounds of the present work, nor is in the scopes of this article. The interested reader can refer to [10, 11].

However, it is worth noticing that most of the simulations of origami or folded structures consider plates as infinitely stiff (or mechanisms), and the deformations are essentially rigid motions [12, 13] or bar-hinge models [14].

Instead, for deformable plates, one has to solve the governing equations for plates, either for small or large normal deflections w. To introduce the folding lines, one needs to enforce a discontinuity on the rotations of the plate. For this purpose, various researchers introduced internal hinge lines. Numerous works attempted analytical or semi-analytical solutions for the buckling and vibrations of linear elastic plates with internal hinges. In [15], Xiang and co-workers used the Levy’s method (separation of variables) with an assumed trigonometric solution and a domain decomposition method to study the buckling of rectangular plates with through-width internal hinges. The idea is to divide the domain into two parts, provide different solutions for each sub-domain, and then patch the solutions together by imposing the continuity of the displacements, moments and shear forces, but not for the rotations. The subdivision is possible because, in these examples, the folding lines are straight and intersect the boundary of the plate.

This method was successfully used for linear elastic plates. Examples include buckling loads [16], natural vibrations [17] for a first-order shear deformation plate theory. In [18], Grossi used a combination of the Ritz method with Lagrangian multipliers for anisotropic plates and also with curved internal hinge lines [19]. Nonetheless, these methods become less general and cumbersome for von Kármán plates with multiple folding lines that do not allow a domain decomposition. In these cases, numerical methods are easier to use and more versatile.

Several examples of studies of folded plates can be found in the literature, especially in Civil Engineering. It suffices to think that a folded plate is a common architectural building block, for example used for roofs or windows [20]. However, in these cases, the fold is often created as a stress-free ridge in the initial mesh. We will not consider these cases in this paper, as we focus on stress-free flat plates that develop ridge-like deformation a posteriori as the result of applied loads.

Notable examples in the meshfree literature include [21, 22], where the fold geometry is introduced a priori, by joining different plates through boundary conditions. A meshfree method discretises each plate, and the folded plate is an assembly of individual plates.

In this work, instead, we present a method that can handle folding lines that are internal to the plate and does not need to consider a folded plate as an assembly of several plates. In fact, in some cases, it is not possible to separate the domain, for example for complicated folding lines, or folds having a finite length.

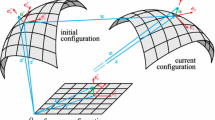
The sketch in Fig. 1 presents the idea of this paper: a fold is a line of discontinuity (indicated with symbol $\llbracket \cdot \rrbracket$) for the rotation fields, like cracks are discontinuities for the displacement fields. We hereby define as infinite folds those lines extending fully across the domain and finite as those folds with extremes within the interior of the domain. In the Mindlin–Reissner kinematics, rotations are discretised with independent shape functions from the displacements. Therefore, introducing a discontinuity in the rotations will generate a folding line. For this reason, the same machinery developed for cracks applies to folding. In this paper, we use a method for cracks in 2D for meshfree methods developed by one of the authors [23].

The paper proceeds as follows: firstly, in Sect. 2 we present the von Kármán theory of plates with large deflections; then, in Sect. 3 we reformulate the problem in weak form; in Sect. 4 we introduce the meshless discretisation and the nonlinear governing equations. In Sect. 5 we show several examples of plates containing single and multiple folds. In particular, we compare the deformations of plate with and without folds. We present two verification examples for a plate with one fold, with the derivation of the analytical solutions presented in “Appendix C”. We also compare the deflection with a reference solution for a simply supported plate with uniform distributed load and for the Euler’s critical buckling load. Finally, in Sect. 6 we draw the conclusions, and point out to the reader the limitations of the method and possible directions for improvement.

Fig. 1

Difference in kinematics between cracks and folds

Fig. 2

The von Kármán plate

2 The von Kármán plate

We define as a plate the following cylinder $\varOmega _0$ in the reference configuration

$$\begin{aligned} \varOmega _0 = \left\{ \mathbf X = (X,Y,Z) \in \mathbb {R}^3: (X,Y) \in \mathcal {S}_0,\ Z \in [-h/2,\ h/2] \right\} \end{aligned}$$

(1)

where $\mathcal {S}_0$ is the mid-plane of the plate and $h$ is the thickness (Fig. 2). Defining $l = \max {(L,b)}$ as a characteristic length of $\mathcal {S}_0$

$$\begin{aligned} \mathcal {O}\left( X\right) =\mathcal {O}\left( Y\right) = l \qquad \mathcal {O}\left( Z\right) =h\qquad \epsilon =\frac{h}{l} \end{aligned}$$

(2)

For thick plates, $\epsilon \ge 10\%$. For these values of $\epsilon$, the Mindlin–Reissner kinematics applies

$$\begin{aligned} u(X,Y,Z)= & {} u_0(X,Y) + Z\ \varphi _{1}(X,Y)\nonumber \\ v(X,Y,Z)= & {} v_0(X,Y) + Z\ \varphi _{2}(X,Y) \nonumber \\ w(X,Y,Z)= & {} w_0(X,Y) \end{aligned}$$

(3)

where $u_0,\, v_0, \, w_0$ are the mid-plane displacements and $\varphi _{1},\, \varphi _{2}$ are the mid-plane rotations. Differently from to the classical von Kármán theory, we consider mid-plane rotations independent from the gradients of $w_0$. We then make the hypothesis of small in-plane strains and moderate rotations, which allows to retain the geometrical non-linearities only for the normal deflection $w_0$ [24]. The Green-Lagrange strain tensor $\mathbf E$ is, in Voigt notation,

$$\begin{aligned} \mathbf E = \begin{bmatrix} E_{11} \\ E_{22} \\ E_{23} \\ E_{13} \\ E_{12} \end{bmatrix}= & {} \begin{bmatrix} \dfrac{\partial u_0}{\partial X} + \frac{1}{2} \left( \dfrac{\partial w_0}{\partial X} \right) ^2 \\ \dfrac{\partial v_0}{\partial Y} + \frac{1}{2} \left( \dfrac{\partial w_0}{\partial Y} \right) ^2 \\ \dfrac{\partial w_0}{\partial Y} + \varphi _{2} \\ \dfrac{\partial w_0}{\partial X} + \varphi _{1} \\ \dfrac{\partial u_0}{\partial Y} + \dfrac{\partial v_0}{\partial X} + \dfrac{\partial w_0}{\partial X}\dfrac{\partial w_0}{\partial Y} \end{bmatrix} \nonumber \\&+\, Z\, \begin{bmatrix} \dfrac{\partial \varphi _{1}}{\partial X} \\ \dfrac{\partial \varphi _{2}}{\partial X} \\ 0 \\ 0 \\ \dfrac{\partial \varphi _{1}}{\partial Y} + \dfrac{\partial \varphi _{2}}{\partial X} \end{bmatrix} =\mathbf E _0 + Z\, \varvec{\kappa } \end{aligned}$$

(4)

where $\mathbf E _0$ is the Green-Lagrange strain tensor of the mid-plane and $\varvec{\kappa }$ is the curvature of the mid-plane. The constitutive model for the von Kármán plate is linear isotropic elastic material, with E being the Young’s modulus and $\nu$ is the Poisson ratio. The Second Piola-Kirchhoff stress is given by

$$\begin{aligned} \mathbf S= & {} \mathbf D \, \mathbf E = \frac{E}{1-\nu ^2}\, \begin{bmatrix} 1&\quad \nu&\quad 0&\quad 0&\quad 0 \\ \nu&\quad 1&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad 1-\nu&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad 1-\nu&\quad 0 \\ 0&\quad 0&\quad 0&\quad 0&\quad 1-\nu \\ \end{bmatrix} \nonumber \\&\times \left( \mathbf E _0 + Z\, \varvec{\kappa } \right) \end{aligned}$$

(5)

with $\mathbf D$ is the stiffness tensor.

3 Weak form of the equations

The problem is then formulated as: find the displacement field $\mathbf u = \begin{bmatrix} u(X,Y,Z)&v(X,Y,Z)&w(X,Y,Z) \end{bmatrix}^T$ such that

$$\begin{aligned} \mathbf u = \arg \min _\mathbf{u \in \mathcal {H}^1\left( \varOmega _0\right) } \varPi \left[ \mathbf u \right] \end{aligned}$$

(6)

where $\mathcal {H}^1\left( \varOmega _0\right)$ is the space of vectorial functions in $\mathcal {L}^2\left( \varOmega _0\right)$ that are square-integrable along with their first derivatives; $\varPi \left[ \mathbf u \right]$ is the potential energy functional, defined as

$$\begin{aligned} \varPi \left[ \mathbf u \right] = \mathcal {U}\left[ \mathbf u \right] -\mathcal {P}\left[ \mathbf u \right] \end{aligned}$$

(7)

where $\mathcal {U}\left[ \mathbf u \right]$ is the the internal energy functional

$$\begin{aligned} \mathcal {U}\left[ \mathbf u \right] = \int _{\varOmega _0} W( \mathbf E ) \hbox {d}V \end{aligned}$$

(8)

where $W$ is the strain energy function; $\mathcal {P}\left[ \mathbf u \right]$ is the external work functional (in absence of body forces)

$$\begin{aligned} \mathcal {P}\left[ \mathbf u \right] = \lambda \int _{\varGamma _t^0} \hat{\mathbf{t }}_0^T\mathbf u \ \hbox {d}S + \gamma \int _{\varGamma _u^0} \left( \mathbf u - \alpha \, \bar{\mathbf{u }}\right) ^T\left( \mathbf u - \alpha \, \bar{\mathbf{u }}\right) \ \hbox {d}S \end{aligned}$$

(9)

and $\lambda$ is the load level; the boundary $\varGamma ^{0}_{t} \subset \partial \varOmega _0$ is where the traction $\lambda \ \hat{\mathbf{t }}_0$ is prescribed, with $\hat{\mathbf{t }}_0$ being a unit vector and $\lambda$ the load level; $\varGamma ^{0}_{u} \subset \partial \varOmega _0$ is the boundary where the displacement $\bar{\mathbf{u }}$ is prescribed, with $\alpha$ being the load level for the applied displacements and $\gamma$ is a penalty factor.

Equation (6) can be reformulated as

$$\begin{aligned} \delta \varPi \left[ \delta \mathbf u ,\mathbf u \right] = \delta \mathcal {U}\left[ \delta \mathbf u ,\mathbf u \right] - \delta \mathcal {P}\left[ \delta \mathbf u ,\mathbf u \right] = 0 \end{aligned}$$

(10)

where $\delta$ indicates a variation

$$\begin{aligned} \delta \mathcal {U}\left[ \delta \mathbf u ,\mathbf u \right]= & {} \int _{\varOmega _0} \delta \mathbf E ^T \mathbf S \ \hbox {d}V \end{aligned}$$

(11)

$$\begin{aligned} \delta \mathcal {P}\left[ \delta \mathbf u ,\mathbf u \right]= & {} \lambda \int _{\varGamma _t^0} \hat{\mathbf{t }}_0^T\ \delta \mathbf u \ \hbox {d}S + \gamma \int _{\varGamma _u^0} \ \delta \mathbf u ^T\left( \mathbf u - \alpha \, \bar{\mathbf{u }}\right) \ \hbox {d}S\nonumber \\ \end{aligned}$$

(12)

Integrating over the thickness, the variation (11) becomes

$$\begin{aligned} \delta \mathcal {U}\left[ \delta \mathbf u ,\mathbf u \right] = \int _{\mathcal {S}_0} \delta \mathbf E _0^T\mathbf N \, \hbox {d}S + \int _{\mathcal {S}_0} \delta \varvec{\kappa }^T\mathbf M \, \hbox {d}S \end{aligned}$$

(13)

where

$$\begin{aligned} \mathbf N = h\, \mathbf D \,\mathbf E _0 \qquad \mathbf M =\frac{h^3}{12} \mathbf D \,\varvec{\kappa } \end{aligned}$$

(14)

with $\mathbf S$ given by Eq. (5). A shear correction factor of 5 / 6 multiplies the transverse shear forces $N_{23}$ and $N_{13}$ to take into account the through-thickness parabolic variation of the transverse shear stress, as predicted by the three-dimensional theory, because the Mindlin–Reissner kinematics predicts a constant transverse shear stress [24].

Also,

$$\begin{aligned} \delta \mathcal {P}\left[ \delta \mathbf u ,\mathbf u \right]= & {} \lambda \int _{\mathcal {L}^0_t} \delta u_{0N}^T \mathcal {N}_N\, \hbox {d}l + \lambda \int _{\mathcal {L}^0_t} \delta u_{0T}^T \mathcal {N}_T\, \hbox {d}l\nonumber \\&+\, \lambda \int _{\mathcal {L}^0_t} \delta u_{0Z}^T \mathcal {N}_Z\, \hbox {d}l + \lambda \int _{\mathcal {L}^0_t} \delta \varphi _{N}^T \mathcal {M}_N\, \hbox {d}l \nonumber \\&+\, \lambda \int _{\mathcal {L}^0_T} \delta \varphi _{T}^T \mathcal {M}_T\, \hbox {d}l \nonumber \\&+\, \gamma \, h\, \int _{\mathcal {L}^0_u} \delta u_{0N}^T \left( u_{0N} - \alpha \,\bar{u}_{0N} \right) \hbox {d}l \nonumber \\&+\, \gamma \, h\, \int _{\mathcal {L}^0_u} \delta u_{0T}^T \left( u_{0T} - \alpha \,\bar{u}_{0T} \right) \hbox {d}l \nonumber \\&+\, \gamma \, h\, \int _{\mathcal {L}^0_u} \delta u_{0Z}^T \left( u_{0Z} - \alpha \, \bar{u}_{0Z} \right) \hbox {d}l +\nonumber \\&+\, \gamma \, \frac{h^3}{12}\,\int _{\mathcal {L}^0_u} \delta \varphi _{0T}^T \left( \varphi _{0T} - \alpha \, \bar{\varphi }_{0T} \right) \hbox {d}l \nonumber \\&+\, \gamma \, \frac{h^3}{12}\, \int _{\mathcal {L}^0_u} \delta \varphi _{0N}^T \left( \varphi _{0N} - \alpha \, \bar{\varphi }_{0N} \right) \hbox {d}l \end{aligned}$$

(15)

where $\mathcal {L}^0_t$ is such that $\varGamma _t^0 = \mathcal {L}^0_t \times [-h/2, h/2]$, $\mathcal {L}^0_u$ is such that $\varGamma _u^0 = \mathcal {L}^0_u \times [-h/2, h/2]$, the subscript $(\cdot )_N$ and $(\cdot )_T$ respectively indicate the normal and tangential direction of $\mathcal {L}^0_t$ in the reference configuration, while the subscript $(\cdot )_Z$ means the through-thickness direction; the bar $\bar{( \cdot )}$ indicates applied displacements and rotations ; the symbols $\mathcal {N}$ and $\mathcal {M}$ indicate respectively the stress resultants and the moment resultants over the thickness of $\hat{\mathbf{t }}_0$.

4 The discretization of the weak form

We will use a meshfree setting, namely the Reproducing Kernel Particle Method (RKPM) [25], combined with the intrinsic enrichment presented in [23, 26, 27] to introduce discontinuities in the rotations.

The mid-plane $\mathcal {S}_0$ is discretized with a cover of N overlapping spheres $\mathcal {Q}_I \subset \mathcal {S}_0$ of variable radii $r_I, \ I=1,\ldots ,N$, such that $\mathcal {S}_0\subset \bigcup _{I=1}^{N} \mathcal {Q}_I$. We call nodes the centres of these spheres $\mathbf X _I$, and we consider H as an average measure of the distance between two neighbouring nodes. Because of the overlap, $H<r_I, \ I=1,\ldots ,N$.

Following a Bubnov-Galerkin method, we approximate test and trial functions as a linear combination of compact support RKPM shape functions.

The functions $u_0^H, \, v_0^H, \, w_0^H, \, \varphi _{1}^H, \, \varphi _{2}^H$ are

$$\begin{aligned} u_0^H (\mathbf X )= & {} \sum _{I=1}^{N} \phi _I(\mathbf X ) \ U_{0_I} \end{aligned}$$

(16)

$$\begin{aligned} v_0^H (\mathbf X )= & {} \sum _{I=1}^{N} \phi _I(\mathbf X ) \ V_{0_I} \end{aligned}$$

(17)

$$\begin{aligned} w_0^H (\mathbf X )= & {} \sum _{I=1}^{N} \phi _I(\mathbf X ) \ W_{0_I} \end{aligned}$$

(18)

$$\begin{aligned} \varphi _{1}^H (\mathbf X )= & {} \sum _{I=1}^{N} \psi _I(\mathbf X ) \ \varPhi _{1_I} \end{aligned}$$

(19)

$$\begin{aligned} \varphi _{2}^H (\mathbf X )= & {} \sum _{I=1}^{N} \psi _I(\mathbf X ) \ \varPhi _{2_I} \end{aligned}$$

(20)

where $U_I, \, V_I, \, W_I, \, \varPhi _{1_I}, \, \varPhi _{2_I}$ are nodal coefficients (not nodal values) and $\phi _I(\mathbf X )$ shape functions centred in $\mathbf X _I$ for the mid-plane displacements and $\psi _I(\mathbf X )$ are the shape functions for the rotations.

Fig. 3

Semi-domains $\mathcal {S}_0^{+}$ and $\mathcal {S}_0^{-}$ created by extending the folding segment $\mathfrak {s}$

Fig. 4

Eligible nodes for enrichment: black thick line is the folding line $\mathfrak {s}$, blue dots are the discretisation nodes $\mathbf X _I$ and the blue circles are the horizons of the support. Continuous circles indicate enriched nodes, while the dashed circle is excluded. (Color figure online)

The shape functions are computed as

$$\begin{aligned} \phi _I(\mathbf X ) = \omega (|\mathbf X -\mathbf X _I| ) \mathbf P (\mathbf X )^T \mathsf {M}^{-1}(\mathbf X ) \mathbf P (\mathbf X _I) \end{aligned}$$

(21)

where the weighting function $\omega$ is defined as

$$\begin{aligned} \omega (\xi ) = {\left\{ \begin{array}{ll} 1-6\,\xi ^2+8\, \xi ^3-3\,\xi ^4&{} \qquad 0\le \xi \le 1 \\ 0 &{} \qquad \xi >1 \end{array}\right. } \end{aligned}$$

(22)

The vector $\mathbf P (\mathbf X )$ denotes a complete basis of the subspace of polynomials of degree k,

$$\begin{aligned} \mathbf P (\mathbf X ) = \{p_0(\mathbf X ), p_1(\mathbf X ), \cdots , p_k(\mathbf X ) \} \end{aligned}$$

(23)

Finally, the moment matrix $\mathsf {M}$ is

$$\begin{aligned} {\mathsf {M}}(\mathbf{X }) = \sum _{I\in \mathcal {S}_{\mathbf{X }}^{r}}\omega (\mathbf{X }_I,\mathbf{X }) \mathbf{P }\left( \frac{\mathbf{X }_I - \mathbf{X }}{r}\right) \mathbf{P }^T \left( \frac{\mathbf{X }_I -\mathbf{X }}{r}\right) \end{aligned}$$

(24)

where the index set $\mathcal {S_\mathbf X }^r$

$$\begin{aligned} \mathcal {S_\mathbf X }^r = \big \{J\in \{1,2,\cdots ,N\} \;\;\; | \;\;\; \Vert \mathbf X -\mathbf X _J\Vert \le r_J\big \} \end{aligned}$$

(25)

and r is the average of the radii $r_I$. In the following, we use the empirical rule for the support radii $r = k + 1$ to avoid singularity of the moment matrix.

The moment matrix can be inverted quickly using an iterative algorithm based on the Sherman–Morrison formula [28] which provides explicit equations for $\mathsf {M}^{-1}$ and proved to reduce sensibly the computational costs associated with Eqs. (24) and (21). The same formula (21) stands for $\psi _I(\mathbf X )$.

Fig. 5

Kinked folding line $\mathfrak {s}_1 \cup \mathfrak {s}_2$ intersecting a folding line $\mathfrak {s}_3$: the enrichment is applied iteratively for each segment $\mathfrak {s}_k \ k=1,2,3$

4.1 Weight function enrichment

To introduce a fold, we need to introduce an enrichment in $\psi _I(\mathbf X )$. We use an weight function enrichment, where

$$\begin{aligned} \omega _e(|\mathbf X -\mathbf X _I|) = \omega (|\mathbf X -\mathbf X _I|)\, \bar{e}(\mathbf X ,\mathbf X _I) \end{aligned}$$

(26)

and $\bar{e}$ is the enrichment function. The enrichment function is briefly recalled in “Appendix A” for the convenience of the reader.

Fig. 6

The simply supported plate as in [30]

In Eq. (26), the enrichment $\bar{e}$ depends on the discretization node $\mathbf X _I$ in the following manner: imagine to extend the fold line to reach the boundaries of $\mathcal {S}_0$; this imaginary line splits $\mathcal {S}_0$ into two parts, a positive one $\mathcal {S}_0^{+}$ where $S>0$ and a negative part $\mathcal {S}_0^{-}$, with S being the axis perpendicular to segment $\mathfrak {s}$ (Fig. 3). Applying function e in Eq. (44) to the nodes $\mathbf X _I \in \mathcal {S}_0^{-}$ would simply zero their weight functions. To avoid such occurrence, the weight functions are modified with the complement to 1 of e

$$\begin{aligned} \bar{e}(\mathbf X ,\mathbf X _I) = e(\mathbf X )\, \mathcal {H}\left( S_I \right) +\Big (1-e(\mathbf X )\Big )\, \mathcal {H}\left( -S_I\right) \end{aligned}$$

(27)

The enrichment in Eq. (27) is applied only to those nodes whose support is cut by the folding line:

$$\begin{aligned} d(\mathbf X _I)<r_I \end{aligned}$$

(28)

as showed in Fig. 4, where d is defined in Eq. (43).

Let us now assume that there exist n folding lines, denoted by $\mathfrak {s}_1, \, \mathfrak {s}_2, \, \ldots \mathfrak {s}_n$. Let $\bar{e}_1, \, \bar{e}_2, \, \ldots \bar{e}_n$ be the respective enrichments. Then, these enrichments apply iteratively to the $\omega$, as shown in Fig. 5:

$$\begin{aligned} \omega _e^{k+1} = \omega _e^{k}\,\bar{e}_{k+1} \qquad k=0,1, \ldots n-1 \end{aligned}$$

(29)

where $\omega _e^{0} = \omega$. The greatest advantage of the proposed enrichment is that Eq. (29) applies also for intersecting folding lines. However, care must be taken in choosing an appropriate $r_I$ for each node, or an appropriate nodal spacing H, to avoid singularity of the moment matrix (Eq. (24)).

4.2 Discretised equations of motion

Substituting Eqs. (16), (17), (18), (19) and (20) into Eqs. (13) and (15), and eliminating the variation of the nodal values, we arrive at

$$\begin{aligned} \mathbf F ^{(i)}(\mathbf d ) - \lambda \, \mathbf F ^{(e)}(\mathbf d ) + \gamma \, \mathbf F ^{(r)}(\alpha ,\, \mathbf d ) = 0 \end{aligned}$$

(30)

where $\mathbf F ^{(i)}$ is the internal force vector

$$\begin{aligned} \mathbf F ^{(i)}(\mathbf d ) = \int _{\mathcal {S}_0} \mathbf B (\mathbf d )^T \mathbf N \, \hbox {d}S + \int _{\mathcal {S}_0} \varvec{\beta }^T \mathbf M \, \hbox {d}S \end{aligned}$$

(31)

Fig. 7

Comparison of the numerical results with [30]: $w_m$ is the negative vertical displacements of the central point (L / 2, L / 2) of the plate

with matrix $\mathbf B$ being

$$\begin{aligned} \mathbf B =\begin{bmatrix} \dfrac{\partial \varvec{\phi }^T}{\partial X}&\quad 0&\quad \dfrac{\partial \varvec{\phi }^T}{\partial X}\, \dfrac{\partial w_0}{\partial X}&\quad 0&\quad 0 \\ 0&\quad \dfrac{\partial \varvec{\phi }^T}{\partial Y}&\quad \dfrac{\partial \varvec{\phi }^T}{\partial Y}\, \dfrac{\partial w_0}{\partial Y}&\quad 0&\quad 0 \\ 0&\quad 0&\quad \dfrac{\partial \varvec{\phi }^T}{\partial Y}&\quad 0&\quad \varvec{\psi }^T \\ 0&\quad 0&\quad \dfrac{\partial \varvec{\phi }^T}{\partial X}&\quad \varvec{\psi }^T&\quad 0 \\ \dfrac{\partial \varvec{\phi }^T}{\partial Y}&\quad \dfrac{\partial \varvec{\phi }^T}{\partial X}&\quad \dfrac{\partial \varvec{\phi }^T}{\partial Y}\dfrac{\partial w_0}{\partial X} + \dfrac{\partial \varvec{\phi }^T}{\partial X}\dfrac{\partial w_0}{\partial Y}&\quad 0&\quad 0 \end{bmatrix} \end{aligned}$$

(32)

and $\varvec{\beta }$

$$\begin{aligned} \varvec{\beta } =\begin{bmatrix} 0&\quad 0&\quad 0&\quad \dfrac{\partial \varvec{\psi }^T}{\partial X}&\quad 0 \\ 0&\quad 0&\quad 0&\quad 0&\quad \dfrac{\partial \varvec{\psi }^T}{\partial Y} \\ 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad \dfrac{\partial \varvec{\psi }^T}{\partial Y}&\quad \dfrac{\partial \varvec{\psi }^T}{\partial X} \end{bmatrix} \end{aligned}$$

(33)

and

$$\begin{aligned} \mathbf N= & {} \begin{bmatrix} N_{XX} \\ N_{YY} \\ Q_Y \\ Q_X \\ N_{XY} \end{bmatrix} \qquad \mathbf M =\begin{bmatrix} M_{XX} \\ M_{YY} \\ 0 \\ 0 \\ M_{XY} \end{bmatrix} \end{aligned}$$

(34)

$$\begin{aligned} \mathbf F ^{(e)}(\mathbf d )= & {} \begin{bmatrix} \int _{\mathcal {L}^0_t} \varvec{\phi }\, \left( \mathcal {N}_{XX}\, n_X +\mathcal {N}_{XY}\, n_Y \right) \hbox {d}l \\ \int _{\mathcal {L}^0_t} \varvec{\phi }\, \left( \mathcal {N}_{XY}\, n_X +\mathcal {N}_{YY}\, n_Y \right) \hbox {d}l \\ \int _{\mathcal {L}^0_t} \varvec{\phi }\, \left[ \left( \mathcal {Q}_X +\mathcal {N}_{XX}\, \dfrac{\partial w_0}{\partial X} + \mathcal {N}_{XY}\, \dfrac{\partial w_0}{\partial Y} \right) \, n_X \, + \left( \mathcal {Q}_Y + \mathcal {N}_{XY}\, \dfrac{\partial w_0}{\partial X} + \mathcal {N}_{YY}\, \dfrac{\partial w_0}{\partial Y} \right) \right] \hbox {d}l \\ \int _{\mathcal {L}^0_t} \varvec{\psi }\left( \mathcal {M}_{XX}\, n_X + \mathcal {M}_{XY}\, n_Y \right) \hbox {d}l \\ \int _{\mathcal {L}^0_t} \varvec{\psi }\left( \mathcal {M}_{XY}\, n_X +\mathcal {M}_{YY}\, n_Y \right) \hbox {d}l \end{bmatrix} \end{aligned}$$

(35)

where $\mathcal {N}_{(\cdot ,\cdot )}$ are the applied in-plane normal forces per unit-length, $\mathcal {M}_{(\cdot ,\cdot )}$ are the applied moments per unit-length and $\mathcal {Q}_{(\cdot )}$ are the applied shear forces per unit-length. The subscripts refer to the X and Y axis in the reference configuration and $n_X,\, n_Y$ are the components of the normal unit vector of curve $\mathcal {L}^0_t$. Finally,

$$\begin{aligned} \mathbf F ^{(r)}(\mathbf d , \, \alpha ) =\begin{bmatrix} \int _{\mathcal {L}^0_u} \varvec{\phi }\, \left( u_0 - \alpha \, \bar{u}_{0} \right) \hbox {d}l \\ \int _{\mathcal {L}^0_u} \varvec{\phi }\, \left( v_0 - \alpha \, \bar{v}_{0} \right) \hbox {d}l \\ \int _{\mathcal {L}^0_u} \varvec{\phi }\, \left( w_0 - \alpha \, \bar{w}_{0} \right) \hbox {d}l \\ \int _{\mathcal {L}^0_u} \varvec{\psi }\, \left( \varphi _1 - \alpha \, \bar{\varphi }_{1} \right) \hbox {d}l \\ \int _{\mathcal {L}^0_u} \varvec{\psi }\, \left( \varphi _2 - \alpha \, \bar{\varphi }_{2} \right) \hbox {d}l \end{bmatrix} \end{aligned}$$

(36)

Whenever the load level $\lambda$ or $\alpha$ is not provided, such as in tracing bifurcation diagrams, one more equation is necessary. The closure of Eq. (30) is the arc-length constraint

$$\begin{aligned} g(\mathbf d ,\lambda ) = \sqrt{\varDelta \mathbf d ^T\varDelta \mathbf d }/l - 1 = 0 \end{aligned}$$

(37)

Fig. 8

Structured discretisation used in the numerical examples: continuous grey lines are the quadrature cells, small red dots are the Gaussian points and larger blue dots are the discretisation nodes. (Color figure online)

Fig. 9

The simply supported plate as in [30] with fourfolds

Fig. 10

Comparison of the numerical results of the plate in Fig. 7 with folds and no folds

where l is the arc-length parameter, and $\varDelta \mathbf d = \mathbf d -\mathbf d _0$, where $\mathbf d _0$ is a previously converged state. We solve the nonlinear equations with a quasi-Newton trust-region algorithm for sparse problems [29], with a provided sparsity pattern for the Jacobian to speed up the iterations. Both Eqs. (30) and (37) are normalized, so that the error in each iteration is expressed as a percentage. The convergence is usually achieved within machine precision in 4 or 5 iterations.

5 Numerical examples

5.1 Simply supported plate without and with folds

We first solved a classic benchmark example (Fig. 6) for the von Kármán plate, with the aim of identifying the optimal number of nodes and the order of the basis in Eq. (23). All the quantities are appropriately normalised to obtain a dimensionless problem: $L = 1\, \hbox {m},\, E=1\, \hbox {Pa}, \, \nu =0.316, \, h/L=0.1$. All four edges are simply supported, $u_0=v_0=w_0 = 0$. A normal uniform pressure p is applied on the mid-plane. The direction of the load is fixed, i.e. it does not follow the deformed normal direction of the plate.

“Appendix B” reports a detailed analysis on the number of nodes, order of quadrature, number of quadrature cells and order of polynomial basis for this problem. For simplicity, we used structured discretisations (Fig. 8), although the method is applicable also to unstructured discretisations. In this section we report the main findings. It turns out that a good convergence of 15 nodes per side of the plate is obtained for various thickness-to-length ratios if a full third-order polynomial basis is used. Contrarily to finite elements, the use of such a high order basis can be easily obtained with an RKPM approximation. In addition, we use 60 first-order rule Gaussian quadrature cells per length. Figure 7 shows a comparison with a semi-analytical (yet approximate) solution derived from a Fourier series expansion of the vertical deflection $w_0$ [30]. A third-order basis also seems to alleviate shear-locking issues as the thickness of the plate becomes small. Figure 7 shows no degradation of the solution even for $h/L=1\, \%$. Therefore, in the following examples, unless otherwise stated, we will use a third-order basis and the same nodal spacing. To better capture the kinematics of a plate containing multiple folds and to avoid singularities of the moments matrix, as a precaution, we use 25 nodes per side of the plate and 100 quadrature cells per side of the plate (Fig. 8).

Fig. 11

Deformation and rotation field $\varphi _{1}(X,Y)$ for the example in Fig. 6 for a load $\frac{p}{E}\left( \frac{L}{h}\right) ^4 = 200$ (colorbar indicates angles in degrees and it is the same for both figures). In Fig. 11b, the fold lines are clearly visible as discontinuities in $\varphi _{1}(X,Y)$. (Color figure online)

Fig. 12

Numerical results for the verification of the method: colors show $\varphi _{1}(X,Y)$. Both beams have a fold in the middle with dihedral angle $\varphi _0$. The sharp contrast in color indicates a discontinuity in $\varphi _{1}(X,Y)$. (Color figure online)

Next, we keep the same plate and boundary conditions, but we add fourfolds as in Fig. 9. The effect of the folds is clearly visible in Fig. 10: for the same load p, the vertical deflection is smaller than the one for the plate with no folds. This stiffening agrees with the intuition: a flat thin sheet of paper will bend under its own weight. But, if the sheet of paper contains folds, it will bend less (or not bend at all) (Fig. 11).

Fig. 13

Error norm $\mathcal {L}_2$ for the transverse displacement w (red line) and the rotation $\varphi _{1}$ (blue line) for the solution in Eq. (50). (Color figure online)

Fig. 14

Error norm $\mathcal {L}_2$ for the transverse displacement w (red line) and the rotation $\varphi _{1}$ (blue line) for the solution in Eq. (53). (Color figure online)

Fig. 15

Rectangular plate with folds in the middle and applied rotations

Fig. 16

Deformation and $\varphi _{1}$ for a rectangular plate with and without central fold in the middle. The load is a couple of symmetric applied rotations at the left and right edge. The colorbar indicate the angles in degrees. (Color figure online)

5.2 Verification of the method

We verified the method against analytical solutions obtained from the Euler–Bernoulli beam Eq. (45). We assumed that a fold exists in the middle of the beam. We considered two cases: an unloaded simply supported beam and a beam loaded only by a bending moment. The first one is with the beam at its rest state, and consists in a roof-like deformation (Eq. (50) and Fig. 12a) with no curvature; the second solution (Eq. (53) and Fig. 12b) has a uniform non-zero curvature with a cusp at the fold line. For both cases, we computed the $\mathcal {L}_2$ norm of the error:

$$\begin{aligned} || e_w ||_{\mathcal {L}_2} = \displaystyle \frac{\sqrt{\int _{\mathcal {S}_0} \ (w-w_0^H)^2 \ \hbox {d}S}}{\sqrt{\int _{\mathcal {S}_0} \ w^2 \ \hbox {d}S}} \end{aligned}$$

(38)

with $w_0^H$ given by Eq. (18) and w being the exact solution given in “Appendix C”. We also evaluated the error for the rotations

$$\begin{aligned} || e_{\varphi _{1}} ||_{\mathcal {L}_2} = \displaystyle \frac{\sqrt{\int _{\mathcal {S}_0} \ (\theta -\varphi _{1}^H)^2 \ \hbox {d}S}}{\sqrt{\int _{\mathcal {S}_0} \ \theta ^2 \ \hbox {d}S}} \end{aligned}$$

(39)

with $\varphi _{1}^H$ given by Eq. (19) and $\theta$ is the exact solution given in “Appendix C”.

Fig. 17

Deformation and $\varphi _{1}$ for a rectangular plate with two inclined edge folds in the middle and with two kinked edge folds. The load is a couple of symmetric applied rotations at the left and right edge. The colorbar indicate the angles in degrees. (Color figure online)

Fig. 18

Rectangular plate with a central horizontal fold over the length and three vertical half-width folds. The transverse deflection is constrained over the vertical folds. (Color figure online)

The order of reproducibility of the shape functions is 1 and the order of quadrature is 1. The number of quadrature cells per shorter side of the plate is always 4 times the number of nodes (per shorter side of the plate). We kept the same H in both axes: for example, if n is the number of nodes on the shorter side (in this case b, y-axis), the number of nodes in the x-axis is $L/b\,n$.

All the quantities are appropriately normalised to obtain a dimensionless problem: $L = 1\, \hbox {m},\, b=h=0.1\, \hbox {m}, \ E=1\, \hbox {Pa}, \, \nu =0.3, \, h/L=0.1$. The dihedral angle of the fold (the amplitude of the discontinuity in the rotations) was set at $\varphi _0=\pi /10$.

Figure 13 shows the percentage error for different nodal spacing H: even with a small number of nodes (3) along the y-axis $(H=b/2)$ the percentage error is $0.1965\%$ for the displacements and $0.1699\%$ for the rotations.

Figure 14 shows the error in the displacements and rotations for the second case (Eq. (53)) considered for the verification. Also in this case, the errors are very small: for example, with $(H=b/2)$ the percentage error is $0.5785\%$ for the displacements and $0.5176\%$ for the rotations.

5.3 Rectangular plate with folds in the middle

Next, we show more explicitly the effect of the enrichment in a plate by inserting one or more folds in the middle. We construct an ad-hoc example as in Fig. 15. Firstly, we consider a flat rectangular plate, with a fold straight line in the middle. On this line, all mid-plane displacements are fixed Also, at the left ($X=0$) and right edge ($X=L$) symmetric rotations $\bar{\varphi _{1}}$ are applied. For this example, $b/L = 0.4$ and $h/L = 0.1$. The material properties are the same as in Sect. 5.1. Figure 16a shows the deformation of the plate without a fold: the rotation field $\varphi _{1}(X,Y)$ is smooth and continuous, and the deformation shows no kinks. Instead, with a fold in the middle, the rotation field is discontinuous (Fig. 16b) and the deformation shows a ridge.

The enrichment allows the introduction of multiple and kinked folds, and Fig. 17 show the same example with two inclined parallel infinite folds separated by L / 8 and a central fold composed by two lines with a kink in the middle.

5.4 Buckling of plates with folds

This example is the plate shown in Fig. 18. The plate contains fourfolds, one is a central horizontal fold running through the length, and the remaining three are vertical, long half the width of the plate, staggered and separated by L / 4. On these last threefolds, the transverse deflection is fixed. The plate contains an initial imperfection on the right and left edges, as an initial applied rotation $\alpha =5^{\circ }$. A compressive load $\lambda$ is applied on the right edge. The presence of the folds increases the critical Euler’s load, since the effective length is the distance between the vertical fold lines L / 4

$$\begin{aligned} P_c = \pi ^2 \frac{E\, I}{\left( \frac{L}{4}\right) ^2} \end{aligned}$$

(40)

Fig. 19

Force-displacement curve of the plate with folds during buckling: $P = \lambda \, b P_c$ is the critical Euler’s load, u is the displacement of the loaded edge

Fig. 20

Deformation of the plate with folds during buckling at different loading levels, as in Fig. 19

with I being the minimum area moment of inertia of the cross section. Figure 19 shows the load-displacement curve, with the load approaching asymptotically the critical load. The deformation stages are displayed in Fig. 20, where the fold lines create a shiny reflection in the deformed mid-plane surface.

6 Conclusions, limitations and future directions

This paper demonstrated a meshless approach to the simulations of folds in nonlinear von Kármán plates. The folding lines in this paper can be infinite (extending throughout the mid-plane) or finite (with end-points internal to the mid-plane) folds. We showed examples of plates containing multiple folds of straight or kinked shape.

The main conclusion of the article is that with the same methods developed for cracks, it is possible to simulate folding of plates. In fact, folds are discontinuities in the rotations, just like cracks are discontinuities in the displacements. Therefore, if one has a method for reproducing discontinuous shape functions, it is possible to use such method to discretise the rotation fields.

For this reason, we believe that this paper can bridge the fields of computational fracture mechanics and computational structural instabilities. Imagine all the vast literature of numerical methods for fracture mechanics that can now be used to simulate folding of structures, which includes the realm of origami mechanics.

Possible future directions include the application of methods such eXtended Finite Element (XFEM) [31], cracking particles [32], phase fields [33, 34] and isogeometric analysis [35, 36] to folding.

This approach, of course, is possible if the shape functions approximating the rotations are different from the ones used for displacements. This is the case of thick plates, which possess Mindlin–Reissner kinematics. For thin plates, therefore, a possible future direction could be the introduction of discontinuities directly into the derivatives of the shape functions. Examples include intrinsic [37] or extrinsic enrichments [38, 39].

Using Mindlin–Reissner kinematics for thin plates might generate shear locking issues. However, owing to the merits of the RKPM approximation, the use of a higher-order reproducibility allowed good accuracy even to thin plates, with aspect ratio $h/L=0.01$. Of course, we do not claim that this is a solution to the shear locking issue: a more thorough analysis of this problem is outside the scopes of the paper. We refer to the works of [40,41,42] for a detailed analysis of the shear locking issue in meshfree methods.

Appendices

A Enrichment function

Fig. 21

Segment $\mathfrak {s}$ and coordinates system $T-S$

Fig. 22

Distance function of segment $\mathfrak {s}$ and enrichment

Fig. 23

Comparison of the numerical results with [30] for variable number of nodes: $h/L=0.1$, reproducibility order $k=1$, quadrature rule of order 1. The number of quadrature cells is 4 times the number of the nodes

Fig. 24

Comparison of the numerical results with [30] for variable number of nodes: $h/L=0.05$, reproducibility order $k=1$, quadrature rule of order 1. The number of quadrature cells is 4 times the number of the nodes

Consider a segment $\mathfrak {s} \subset \mathcal {S}_0$ with endpoints $(X_1,Y_1)$ and $(X_2,Y_2)$, midpoint $(X_m,Y_m)$ and length $L_{\mathfrak {s}}$. Define axis T collinear with $\mathfrak {s}$ and S perpendicular to it, with origin in $(X_m,Y_m)$ (Fig. 21). The one-dimensional signed distance function of the endpoints along T is

$$\begin{aligned} d_s^{(1)}(T) = \left| T-\frac{L_{\mathfrak {s}}}{2}\right| - \frac{L_{\mathfrak {s}}}{2} \end{aligned}$$

(41)

The positive part of $d_s^{(1)}(T)$ is

$$\begin{aligned} d_+^{(1)}(T) = \frac{|d_s^{(1)}(T)| + d_s^{(1)}(T)}{2} \end{aligned}$$

(42)

The distance function of $\mathfrak {s}$ is

$$\begin{aligned} d(T(X,Y),S(X,Y)) = \sqrt{d_+^{(1)}(T)^2 + S^2} \end{aligned}$$

(43)

and showed in Fig. 22a. The enrichment function is the normal derivative of the distance function

$$\begin{aligned} e = \frac{1}{2}\left( \dfrac{\partial d}{\partial S} +1 \right) = \frac{1}{2} \left( \frac{S}{d} +1 \right) \end{aligned}$$

(44)

and it is showed in Fig. 22b.

Fig. 25

Comparison of the numerical results with [30] for variable number of nodes: $h/L=0.02$, reproducibility order $k=1$, quadrature rule of order 1. The number of quadrature cells is 4 times the number of the nodes

B Analysis on the number of nodes, quadrature rules and reproducibility order

As anticipated in Sect. 5.1, a good comparison with a semi-analytical solution is obtained when using 15 nodes per side of the plate and a first-order quadrature rule for various thickness-to-length ratios, if a full third-order polynomial basis is used.

Fig. 26

Comparison of the numerical results with [30] for variable number of nodes: $h/L=0.01$, reproducibility order $k=1$, quadrature rule of order 1. The number of quadrature cells is 4 times the number of the nodes

Fig. 27

Comparison of the numerical results with [30] for variable number of nodes: $h/L=0.01$, reproducibility order $k=2$, quadrature rule of order 1. The number of quadrature cells is 4 times the number of the nodes

In fact, Figs. 23, 24, 25 and 26 show the degradation of the accuracy with decreasing thickness ratio $h/L$ for RKPM with linear reproducibility order.

Fig. 28

Comparison of the numerical results with [30] for variable number of nodes: $h/L=0.01$, reproducibility order $k=3$, quadrature rule of order 1. The number of quadrature cells is 4 times the number of the nodes

Fig. 29

Comparison of the numerical results with [30] with different quadrature rules (1, 2, 3) for $h/L=0.01$, $15\times 15$ mesh and $60\times 60$ quadrature cells. The reproducibility order is $k=3$

Figures 27 and 28 show instead that, for small thickness ratios, for example $h/L=0.01$, quadratic and cubic order converge faster with the increase in number of nodes: in particular, the cubic order reaches convergence even with 15 nodes per side of the plate. A similar trend is seen for higher thickness ratios, although they are not reported here for the sake of conciseness.

Finally, Fig. 29 shows that when using RKPM with a third order reproducibility, a Gaussian quadrature rule of order 1 is sufficient, provided that the number of cells per side of the plate is 4 times the number of nodes per side of the plate.

C Analytical solutions of the Euler–Bernoulli beam with a fold

Let us consider the Euler–Bernoulli beam

$$\begin{aligned} D\, \dfrac{\hbox {d}^4 w}{\hbox {d}X^4} = q \qquad 0 \le X \le L \end{aligned}$$

(45)

where $D = E\,h^3/12$ is the bending stiffness, with E being the Young Modulus and $h$ the thickness of the plate, $[D]=\hbox {Nm}$, q the distributed load with $[q]=\hbox {N}/\hbox {m}^2$ and L is the length of the beam. We now pass to the dimensionless form using

$$\begin{aligned} \bar{X} = \frac{X}{L} \qquad \bar{w} = \frac{w}{L} \end{aligned}$$

(46)

Fig. 30

Euler–Bernoulli beams with a fold (blue hat) at $X=X_0$. (Color figure online)

Fig. 31

Analytical solutions of the Euler–Bernoulli beams with a fold at $X=1/2$

Equation (45) becomes

$$\begin{aligned} w'''' = \frac{q\, L^3}{D} = \bar{q} \qquad 0 \le X \le L \end{aligned}$$

(47)

where $(\cdot )' = d/d\bar{X}$. To ease the notation, we removed the bar $\left( \bar{\cdot }\right)$ and assumed that all the quantities are dimensionless. For example,

$$\begin{aligned} \theta = w' \qquad M = w'' \qquad S = w''' \end{aligned}$$

(48)

where $\theta$ is the rotation, M is the moment, S is the shear force. Let us assume that a fold exists at $X=X_0$ and consider two cases, shown in Fig. 30.

For an unloaded simply supported beam (Fig. 30a) with a fold of dihedral angle $\varphi _0$, the boundary conditions are

$$\begin{aligned} w(0) =&\, 0 \end{aligned}$$

(49a)

$$\begin{aligned} w'(0) =&\,\varphi _0/2 \end{aligned}$$

(49b)

$$\begin{aligned} M(1) =&\, 0 \end{aligned}$$

(49c)

$$\begin{aligned} S(1) =&\,0 \end{aligned}$$

(49d)

The solution of Eq. (47) is

$$\begin{aligned} w(X) = \frac{\varphi _0}{2}\, X - \varphi _0 \, \langle X - X_0 \rangle \end{aligned}$$

(50)

and rotation

$$\begin{aligned} \theta (X) = \frac{\varphi _0}{2} - \varphi _0\, \mathcal {H}(X-X_0) \end{aligned}$$

(51)

which is a roof-like deformation (Fig. 31a), with $\mathcal {H}(X)$ being the Heaviside function and

$$\begin{aligned} \langle X \rangle = \frac{X+|X|}{2} \end{aligned}$$

(52)

the ramp function.

For a simply supported beam with an applied moment $M_0$ at both ends and $X_0=1/2$, the solution of Eq. (47) is

$$\begin{aligned} W(X) = \frac{M_0}{6}\, \left( 3\, X^2 - 3\, X + \frac{1}{2} - \left| X - \frac{1}{2}\right| \right) \end{aligned}$$

(53)

with rotation

$$\begin{aligned} \theta (X) = \frac{M_0}{6}\left( 6\, X - 3 -\hbox {sign}\left( X-\frac{1}{2} \right) \right) \end{aligned}$$

(54)

shown in Fig. 31b. The discontinuity in the rotations at $X=1/2$ has magnitude

$$\begin{aligned} \varphi _0= \theta \left( \frac{1}{2}^{-}\right) - \theta \left( \frac{1}{2}^{+}\right) = \frac{M_0}{3}. \end{aligned}$$

(55)