Skip to main content
SpringerLink
Log in

Small strain multiphase-field model accounting for configurational forces and mechanical jump conditions

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

A Correction to this article was published on 07 December 2017

This article has been updated

Abstract

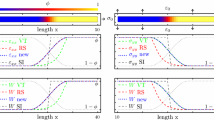
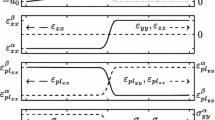
Computational models based on the phase-field method have become an essential tool in material science and physics in order to investigate materials with complex microstructures. The models typically operate on a mesoscopic length scale resolving structural changes of the material and provide valuable information about the evolution of microstructures and mechanical property relations. For many interesting and important phenomena, such as martensitic phase transformation, mechanical driving forces play an important role in the evolution of microstructures. In order to investigate such physical processes, an accurate calculation of the stresses and the strain energy in the transition region is indispensable. We recall a multiphase-field elasticity model based on the force balance and the Hadamard jump condition at the interface. We show the quantitative characteristics of the model by comparing the stresses, strains and configurational forces with theoretical predictions in two-phase cases and with results from sharp interface calculations in a multiphase case. As an application, we choose the martensitic phase transformation process in multigrain systems and demonstrate the influence of the local homogenization scheme within the transition regions on the resulting microstructures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Change history

  • 07 December 2017

    In the original publication, equation 52 was published incorrectly.

References

  1. Chen LQ (2002) Phase-field models for microstructure evolution. Ann Rev Mater Res 32(1):113. https://doi.org/10.1146/annurev.matsci.32.112001.132041

    Article  MathSciNet  Google Scholar 

  2. Moelans N, Blanpain B, Wollants P (2008) An introduction to phase-field modeling of microstructure evolution. Calphad 32(2):268. https://doi.org/10.1016/j.calphad.2007.11.003

    Article  Google Scholar 

  3. van der Waals JD (1894) Thermodynamische Theorie der Kapillarität unter voraussetzung stetiger Dichteänderung. Z Phys Chem Leipzig 13:657

    Google Scholar 

  4. Ginzburg VL, Landau LD (1950) On the theory of superconductivity. Zh Eksp Teor Fiz 20:1064

    Google Scholar 

  5. Cahn JW, Hilliard JE (1958) Free energy of a nonuniform system. I. interfacial free energy. The J Chem Phys 28(2):258. https://doi.org/10.1063/1.1744102

    Article  Google Scholar 

  6. Halperin B, Hohenberg P, Ma S (1974) Renormalization-group methods for critical dynamics: I. Recur Relat Eff Energy Conserv Phys Rev B 10(1):139. https://doi.org/10.1103/PhysRevB.10.139

    Google Scholar 

  7. Steinbach I (2013) Phase-field model for microstructure evolution at the mesoscopic scale. Ann Rev Mater Res 43(1):89. https://doi.org/10.1146/annurev-matsci-071312-121703

    Article  Google Scholar 

  8. Nestler B, Choudhury A (2011) Phase-field modeling of multi-component systems. Curr Opin Solid State and Mater Sci 15(3):93. https://doi.org/10.1016/j.cossms.2011.01.003

    Article  Google Scholar 

  9. Ammar K, Appolaire B, Cailletaud G, Forest S (2009) Combining phase field approach and homogenization methods for modelling phase transformation in elastoplastic media. Revue européenne de mécanique numérique 18(5–6):485. https://doi.org/10.3166/ejcm.18.485-523

    MATH  Google Scholar 

  10. Khachaturyan AG (1983) Theory of structural transformation in solids. John Wiley & Sons Inc, Hoboken

    Google Scholar 

  11. Voigt W (1889) Über die Beziehung zwischen den beiden Elastizitätskonstanten isotroper Körper. Annalen der Physik 274(12):573

    Article  MATH  Google Scholar 

  12. Spatschek R, Müller-Gugenberger C, Brener E, Nestler B (2007) Phase field modeling of fracture and stress-induced phase transitions. Phys Rev E 75(6):066111. https://doi.org/10.1103/PhysRevE.75.066111

    Article  MathSciNet  Google Scholar 

  13. Mennerich C, Wendler F, Jainta M, Nestler B (2011) A phase-field model for the magnetic shape memory effect. Arch Mech 63:549

    MathSciNet  Google Scholar 

  14. Schneider D, Selzer M, Bette J, Rementeria I, Vondrous A, Hoffmann MJ, Nestler B (2014) Phase-field modeling of diffusion coupled crack propagation processes. Adv Eng Mater 16(2):142. https://doi.org/10.1002/adem.201300073

    Article  Google Scholar 

  15. Schneider D, Schmid S, Selzer M, Böhlke T, Nestler B (2015) Small strain elasto-plastic multiphase-field model. Comput Mech 55(1):27. https://doi.org/10.1007/s00466-014-1080-7

    Article  MathSciNet  MATH  Google Scholar 

  16. Schneider D, Schoof E, Huang Y, Selzer M, Nestler B (2016) Phase-field modeling of crack propagation in multiphase systems. Comput Methods in Appl Mech Eng 312:186–195. https://doi.org/10.1016/j.cma.2016.04.009

    Article  MathSciNet  Google Scholar 

  17. Levitas VI (2013) Thermodynamically consistent phase field approach to phase transformations with interface stresses. Acta Mater 61(12):4305. https://doi.org/10.1016/j.actamat.2013.03.034

    Article  Google Scholar 

  18. Reuss A (1929) Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizittitsbedingung fiir Einkristalle. Z Angew Math Mech 9:49

    Article  MATH  Google Scholar 

  19. Steinbach I, Apel M (2006) Multi phase field model for solid state transformation with elastic strain. Phys D 217:153. https://doi.org/10.1016/j.physd.2006.04.001

    Article  MATH  Google Scholar 

  20. Apel M, Benke S, Steinbach I (2009) Virtual dilatometer curves and effective Young’s modulus of a 3D multiphase structure calculated by the phase-field method. Comput Mater Sci 45(3):589. https://doi.org/10.1016/j.commatsci.2008.07.007

    Article  Google Scholar 

  21. Durga A, Wollants P, Moelans N (2013) Evaluation of interfacial excess contributions in different phase-field models for elastically inhomogeneous systems. Modell Simul Mater Sci Eng 21(5):055018. https://doi.org/10.1088/0965-0393/21/5/055018

    Article  Google Scholar 

  22. Schneider D, Tschukin O, Choudhury A, Selzer M, Böhlke T, Nestler B (2015) Phase-field elasticity model based on mechanical jump conditions. Comput Mech 55(5):887. https://doi.org/10.1007/s00466-015-1141-6

    Article  MathSciNet  MATH  Google Scholar 

  23. Schneider D (2017) Phasenfeldmodellierung mechanisch getriebener Grenzflächenbewegungen in mehrphasigen Systemen. Ph.D. thesis

  24. Mosler J, Shchyglo O, Hojjat HM (2014) A novel homogenization method for phase field approaches based on partial rank-one relaxation. J Mech Phys Solids 68:251. https://doi.org/10.1016/j.jmps.2014.04.002

    Article  MathSciNet  MATH  Google Scholar 

  25. Schneider D, Schwab F, Schoof E, Reiter A, Herrmann C, Selzer M, Böhlke T, Nestler B (2017) On the stress calculation within phase-field approaches: a model for finite deformations. Comput Mech (in press). https://doi.org/10.1007/s00466-017-1401-8

  26. Nestler B, Garcke H, Stinner B (2005) Multicomponent alloy solidification: phase-field modeling and simulations. Phys Rev E 71(4):041609. https://doi.org/10.1103/PhysRevE.71.041609

    Article  Google Scholar 

  27. Provatas N, Elder K (2010) Phase-field methods in materials science and engineering. Wiley-VCH Verlag, Weinheim. https://doi.org/10.1002/9783527631520

    Book  Google Scholar 

  28. Nestler B (2000) Phasenfeldmodellierung mehrphasiger Erstarrung. Ph.D. thesis

  29. Hötzer J, Tschukin O, Ben Said M, Berghoff M, Jainta M, Barthelemy G, Smorchkov N, Schneider D, Selzer M, Nestler B (2016) Calibration of a multi-phase field model with quantitative angle measurement. J Mater Sci 51(4):1788. https://doi.org/10.1007/s10853-015-9542-7

    Article  Google Scholar 

  30. Moelans N (2011) A quantitative and thermodynamically consistent phase-field interpolation function for multi-phase systems. Acta Mater 59(3):1077. https://doi.org/10.1016/j.actamat.2010.038

    Article  Google Scholar 

  31. Steinbach I, Pezzolla F (1999) A generalized field method for multiphase transformations using interface fields. Phys D: Nonlinear Phenom 134(4):385. https://doi.org/10.1016/S0167-2789(99)00129-3

    Article  MathSciNet  MATH  Google Scholar 

  32. Eshelby JD (1951) The force on an elastic singularity. Philosophical transactions of the royal society. A: Math Phys Eng Sci 244(877):87–112. https://doi.org/10.1098/rsta.1951.0016

    MathSciNet  MATH  Google Scholar 

  33. Eshelby JD (1975) The elastic energy-momentum tensor. J Elast 5(3–4):321. https://doi.org/10.1007/BF00126994

    Article  MathSciNet  MATH  Google Scholar 

  34. Gurtin ME (1983) Two-phase deformations of elastic solids. Arch Ration Mech Anal 84(1):1–29. https://doi.org/10.1007/BF00251547

    Article  MathSciNet  MATH  Google Scholar 

  35. Gurtin ME (1995) The nature of configurational forces. Arch Ration Mech Anal 131(1):67. https://doi.org/10.1007/BF00386071

    Article  MathSciNet  MATH  Google Scholar 

  36. James RD (1981) Finite deformation by mechanical twinning. Arch Ration Mech Anal 77(2):143–176. https://doi.org/10.1007/BF00250621

    Article  MathSciNet  MATH  Google Scholar 

  37. Johnson WC (1987) Precipitate shape evolution under applied stress thermodynamics and kinetics. Metall Trans A 18A:233

    Article  Google Scholar 

  38. Silhavy M (1997) The Mechanics and thermodynamics of continuous media. Springer Verlag, Berlin

    Book  MATH  Google Scholar 

  39. Voorhees PW, Johnson WC (1986) Interfacial equilibrium during a first-order phase transformation in solids. The J Chem Phys 84(9):5108. https://doi.org/10.1063/1.450664

    Article  Google Scholar 

  40. Gurtin ME (2000) Configurational forces as basic concepts of continuum physics. Springer, Berlin

    MATH  Google Scholar 

  41. Garcke H, Stoth B, Nestler B (1999) Anisotropy in multi-phase systems: a phase field approach. Interfaces and Free Bound 1(2):175–198. https://doi.org/10.4171/IFB/8

    Article  MathSciNet  MATH  Google Scholar 

  42. Johnson WC, Alexander JID (1986) Interfacial conditions for thermomechanical equilibrium in two-phase crystals. J Appl Phys 59(8):2735. https://doi.org/10.1063/1.336982

    Article  Google Scholar 

  43. Mai AK, Singh SJ (1991) Deformation of elastic solids. Prentice-Hall, Upper Saddle River

    Google Scholar 

  44. Wang Y, Khachaturyan AG (2006) Multi-scale phase field approach to martensitic transformations. Mater Sci Eng: A 438–440:55. https://doi.org/10.1016/j.msea.2006.04.123

    Article  Google Scholar 

  45. Mamivand M, Zaeem MA, El Kadiri H (2013) A review on phase field modeling of martensitic phase transformation. Comput Mater Sci 77:304. https://doi.org/10.1016/j.commatsci.2013.04.059

    Article  Google Scholar 

  46. Ueda M, Yasuda HY, Umakoshi Y (2003) Controlling factor for nucleation of martensite at grain boundary in Fe-Ni bicrystals. Acta Mater 51(4):1007. https://doi.org/10.1016/S1359-6454(02)00503-7

    Article  Google Scholar 

  47. Rios PR, Guimarães JRC (2010) Microstructural path analysis of martensite burst. Mater Res 13(1):119. https://doi.org/10.1590/S1516-14392010000100023

    Article  Google Scholar 

  48. Artemev A, Jin Y, Khachaturyan AG (2001) Three-dimensional phase field model of proper martensitic transformation. Acta Mater 49(7):1165. https://doi.org/10.1016/S1359-6454(01)00021-0

    Article  Google Scholar 

  49. Krauss W, Pabi SK, Gleiter H (1989) On the mechanism of martensite nucleation. Acta Metall 37(1):25. https://doi.org/10.1016/0001-6160(89)90262-9

    Article  Google Scholar 

  50. Heo TW, Chen LQ (2014) Phase-field modeling of displacive phase transformations in elastically anisotropic and inhomogeneous polycrystals. Acta Mater 76:68. https://doi.org/10.1016/j.actamat.2014.05.014

    Article  Google Scholar 

  51. Schmidt I, Gross D (1997) The equilibrium shape of an elastically inhomogeneous inclusion. J Mech Phys Solids 45(9):1521. https://doi.org/10.1016/S0022-5096(97)00011-2

    Article  MathSciNet  MATH  Google Scholar 

  52. Kim SG, Kim DI, Kim WT, Park YB (2006) Computer simulations of two-dimensional and three-dimensional ideal grain growth. Phys Rev E 74:061605

    Article  Google Scholar 

  53. B. Nestler, M. Reichert, M. Selzer (2008) Massive multi-phase-field simulations: methods to compute large grain system. In: proceedings of the 11th international conference on aluminium alloys pp. 1251–1255

  54. Vondrous A, Bienger P, Schreijäg S, Selzer M, Schneider D, Nestler B, Helm D, Mönig R (2015) Combined crystal plasticity and phase-field method for recrystallization in a process chain of sheet metal production. Comput Mech 55(2):439. https://doi.org/10.1007/s00466-014-1115-0

    Article  MathSciNet  MATH  Google Scholar 

  55. Hötzer J, Jainta M, Steinmetz P, Nestler B, Dennstedt A, Genau A, Bauer M, Köstler H, Rüde U (2015) Large scale phase-field simulations of directional ternary eutectic solidification. Acta Mater 93:194. https://doi.org/10.1016/j.actamat.2015.03.051

    Article  Google Scholar 

  56. Hötzer J, Steinmetz P, Jainta M, Schulz S, Kellner M, Nestler B, Genau A, Dennstedt A, Bauer M, Köstler H, Rüde U (2016) Phase-field simulations of spiral growth during directional ternary eutectic solidification. Acta Mater 106:249. https://doi.org/10.1016/j.actamat.2015.12.052

    Article  Google Scholar 

  57. Steinmetz P, Yabansu YC, Hötzer J, Jainta M, Nestler B, Kalidindi SR (2016) Analytics for microstructure datasets produced by phase-field simulations. Acta Mater 103:192. https://doi.org/10.1016/j.actamat.2015.09.047

    Article  Google Scholar 

  58. Steinmetz P, Hötzer J, Kellner M, Dennstedt A, Nestler B (2016) Large-scale phase-field simulations of ternary eutectic microstructure evolution. Comput Mater Sci 117:205. https://doi.org/10.1016/j.commatsci.2016.02.001

    Article  Google Scholar 

  59. Bauer M, Rüde U, Hötzer J, Jainta M, Steinmetz P, Berghoff M, Schornbaum F, Godenschwager C, Köstler H, Nestler B (2015) Massively parallel phase-field simulations for ternary eutectic directional solidification. In: proceedings of the international conference for high performance computing pp. 1–12. https://doi.org/10.1145/2807591.2807662

  60. Schmitt R, Kuhn C, Skorupski R, Smaga M, Eifler D, Müller R (2015) A combined phase field approach for martensitic transformations and damage. Arch Appl Mech 85(9–10):1459. https://doi.org/10.1007/s00419-014-0945-8

    Article  MATH  Google Scholar 

Download references

Acknowledgements

We thank the DFG for funding our investigations in the framework of the Research Training Group 1483 and the International Research Training Group 2078. The work was further supported by the state of Baden-Württemberg through the “Mittelbau” program and by the Helmholz program “EMR-Energy efficiency, Materials and Ressources”. The authors gratefully acknowledge the editorial support by Leon Geisen. The authors also thank the referees for their very useful comments.

Author information

Authors and Affiliations

  1. Institute of Applied Materials (IAM-CMS), Karlsruhe Institute of Technology (KIT), Straße am Forum 7, 76131, Karlsruhe, Germany

    Daniel Schneider, Oleg Tschukin, Andreas Reiter, Felix Schwab, Michael Selzer & Britta Nestler

  2. Institute of Materials and Processes (IMP), Karlsruhe University of Applied Sciences, Moltkestrasse 30, 76133, Karlsruhe, Germany

    Daniel Schneider, Ephraim Schoof, Christoph Herrmann, Michael Selzer & Britta Nestler

Authors
  1. Daniel Schneider
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ephraim Schoof
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Oleg Tschukin
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Andreas Reiter
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Christoph Herrmann
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Felix Schwab
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Michael Selzer
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Britta Nestler
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Daniel Schneider.

Additional information

The original version of this article was revised: In the original publication, the equation 52 was published incorrectly and is corrected now.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Schneider, D., Schoof, E., Tschukin, O. et al. Small strain multiphase-field model accounting for configurational forces and mechanical jump conditions. Comput Mech 61, 277–295 (2018). https://doi.org/10.1007/s00466-017-1458-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-017-1458-4

Keywords

Search

Navigation