Skip to main content
SpringerLink
Log in

An approach for simulating microstructures of polycrystalline materials

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

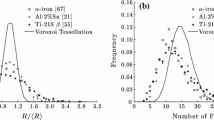
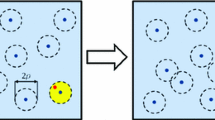
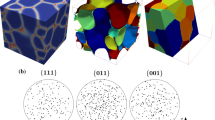
In this paper, an approach is identified using concepts in molecular dynamics (MD) and discrete element method (DEM) to generate the microstructure of polycrystalline materials. Using the proposed methods, different types of particles with different grain size and volume fraction in the real material, can be easily generated. It is assumed that the particles can be randomly packed together into a simulation region, by defining artificial interaction forces among them. Such forces may be either adopted from Van der Waals potential energy, or Hooke pair and gravity forces. The proposed method has proved to be fast due to the fact that the algorithm has been implemented on graphical processing units (GPU). Utilizing the Voronoi tessellation method, the set of the generated discrete grains have been altered to space-filling, adjoining polyhedrons with respect to the real geometry. Moreover, as an advantage, the boundary and the interface region of the microstructures were modeled.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Fan Z, Wu Y, Zhao X, Lu Y (2004) Simulation of polycrystalline structure with Voronoi diagram in Laguerre geometry based on random closed packing of spheres. J Comput Mater Sci 29: 301–308

    Article  Google Scholar 

  2. Weyer S, Frohlich A, Riesch-Oppermann H, Cizelj L, Kovac M (2002) Automatic finite element meshing of planar Voronoi tessellations. J Eng Fract Mech 69: 945–958

    Article  Google Scholar 

  3. Quey R, Dawson PR, Barbe F (2011) Large-scale 3D random polycrystals for the finite element method: generation, meshing and remeshing. J Comput Methods Appl Mech Eng 200: 1729– 1745

    Article  MATH  Google Scholar 

  4. Fritzen F, Bohlke T, Schnack E (2009) Periodic three-dimensional mesh generation for crystalline aggregates based on Voronoi tessellations. J Comput Mech 43: 701–713

    Article  Google Scholar 

  5. Zhang KS, Wu MS, Feng R (2005) Simulation of microplasticity-induced deformation in uniaxially strained ceramics by 3-D Voronoi polycrystal modeling. J Plasticity 21: 801–834

    Article  MATH  Google Scholar 

  6. Rycroft CH, Grest GS, Landry JW, Bazant MZ (2006) Analysis of granular flow in a pebble-bed nuclear reactor. Phys Rev E 74: 45–70

    Article  Google Scholar 

  7. Luther T, Könke C (2009) Poly-crystal models for the analysis of inter-granular crack growth in metallic materials. J Eng Fract Mech 76: 2332–2343

    Article  Google Scholar 

  8. NVIDIA GTX 480 product page (2012). http://www.geforce.com/hardware/desktop-gpus/geforce-gtx-480/specifications

  9. van der Waals JH (1908) Lehrbuch der Thermodynamik, Mass and Van Suchtelen. Leipzig, Part 1

  10. Silbert LE, Ertas D, Grest GS, Halsey TC, Levine D, Plimpton SJ (2001) Granular flow down an inclined plane: Bagnold scaling and rheology. Phys Rev E 64: 051302

    Article  Google Scholar 

  11. Gellatly BJ, Finney JL (1982) Characterization of models of multi-component amorphous metals: the radical alternative to the Voronoi polyhedron. J Non-Cryst Solids 50: 319–329

    Article  Google Scholar 

  12. Ziaei-Rad V, Nouri N, Ziaei-Rad S, Abtahi M (2012) A numerical study on mechanical performance of asphalt mixture using a meso-scale finite element model. J Finite Elem Anal Des 57: 81–91

    Article  Google Scholar 

  13. Mo LT, Huurman M, Wu SP, Molenaar AAA (2008) 2D and 3D meso-scale finite element models for raveling analysis of porous asphalt concrete. J Finite Elem Anal Des 44: 186–196

    Article  Google Scholar 

  14. Calcagnotto M, Ponge D, Demir E, Raabe D (2010) Orientation gradients and geometrically necessary dislocations in ultrafine grained dual-phase steels studied by 2D and 3D EBSD. Mater Sci Eng A 527: 2738–2746

    Article  Google Scholar 

  15. Ohata M, Suzuki M, Ui A, Minami F (2010) 3D-Simulation of ductile failure in two-phase structural steel with heterogeneous microstructure. Eng Fract Mech 77: 277–284

    Article  Google Scholar 

  16. Nouri N, Ziaei-Rad S (2011) A molecular dynamics investigation on mechanical properties of cross-linked polymer networks. Macromolecules 44: 5481–5489

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Isfahan University of Technology, Isfahan, 84156-83111, Iran

    N. Nouri & S. Ziaei-Rad

  2. Department of Civil Engineering, Isfahan University of Technology, Isfahan, 84156-83111, Iran

    V. Ziaei-Rad

Authors
  1. N. Nouri
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. Ziaei-Rad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Ziaei-Rad
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Ziaei-Rad.

Electronic Supplementary Material

The Below is the Electronic Supplementary Material.

ESM 1 (AVI 5582 kb)

ESM 2 (AVI 8654 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Nouri, N., Ziaei-Rad, V. & Ziaei-Rad, S. An approach for simulating microstructures of polycrystalline materials. Comput Mech 52, 181–192 (2013). https://doi.org/10.1007/s00466-012-0805-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-012-0805-8

Keywords

Search

Navigation