Skip to main content
SpringerLink
Log in

Ritz analysis of discontinuous beams using local trigonometric functions

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

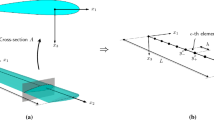
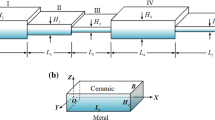
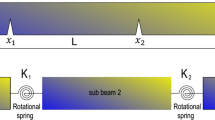
The objective of the current paper is to present a Ritz-type analytical model for predicting the behavior of discontinuous beams such as thin-walled beams with cracks and multiply-stepped beams. The beam is discretized in the cracked as well as the un-cracked domains for a cracked thin-walled beam and in uniform beams for a multiple-stepped beam. A set of local trigonometric trial functions is used to define the twist angle for the cracked domain and the un-cracked domains, as well as to define the displacement field for uniform domains. A global equation system of unknown Ritz coefficients is derived by minimizing the Lagrangian functional or the total potential energy. In the present Ritz model, the interface continuity conditions between sub-domains are investigated and enforced into the global equation system using the condensation procedure or the Lagrange multipliers. Examples are presented to illustrate the effectiveness of the current model for free vibration and torsional analysis. Results obtained from the current model are found to agree well with those obtained using a detailed finite element method or with existing results in literature. The proposed model offers an efficient approach to reduce the modeling efforts and computational time required to analyze complex beams with cracks or multiple steps.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Taleb NJ, Suppiger EW (1961) Vibration of stepped beams. J Aerosp Sci 28: 295–298

    MathSciNet  MATH  Google Scholar 

  2. Buckens F (1963) Eigenfrequencies of nonuniform beams. AIAA J 1: 121–127

    Article  MATH  Google Scholar 

  3. Klein L (1974) Transverse vibrations of non-uniform beams. J Sound Vib 37: 491–505

    Article  Google Scholar 

  4. Maurizi MJ, Belles PM (1993) Free vibration of stepped beams elastically restrained against translation and rotation at one end. J Sound Vib 163: 188–191

    Article  Google Scholar 

  5. Lee HP, Ng TY (1994) Vibration and buckling of a stepped beam. Appl Acoust 42: 257–266

    Article  Google Scholar 

  6. Popplewell N, Daqing Chang (1996) Free vibrations of a complex Euler–Bernoulli beam. J Sound Vib 190: 852–856

    Article  Google Scholar 

  7. Levinson M (1976) Vibrations of stepped strings and beams. J Sound Vib 49: 287–291

    Article  MATH  Google Scholar 

  8. Jang SK, Bert CW (1989) Free vibration of stepped beams: exact and numerical solutions. J Sound Vib 130: 342–346

    Article  Google Scholar 

  9. Jang SK, Bert CW (1989) Free vibration of stepped beams: higher mode frequencies and effects of steps on frequency. J Sound Vib 132: 164–168

    Article  Google Scholar 

  10. Naguleswaran S (2002) Vibration of an Euler–Bernoulli beam on elastic end supports with up to three step changes in cross-section. Int J Mech Sci 44: 2541–2555

    Article  MATH  Google Scholar 

  11. Subramanian G, Balasubramanian TS (1987) Beneficial effects of steps on the free vibration characteristics of beams. J Sound Vib 118: 555–560

    Article  Google Scholar 

  12. Laura PAA, Rossi RE, Pombo JL, Pasqua D (1991) Dynamic stiffening of straight beams of rectangular cross-section: a comparison of finite element predictions and experimental results. J Sound Vib 150: 174–178

    Article  Google Scholar 

  13. Tsukazan T (2005) The use of a dynamical basis for computing the modes of a beam system with a discontinuous cross-section. J Sound Vib 281: 1175–1185

    Article  Google Scholar 

  14. Koplow MA, Bhattacharyya A, Mann BP (2006) Closed form solutions for the dynamic response of Euler–Bernoulli beams with step changes in cross section. J Sound Vib 295: 214–225

    Article  Google Scholar 

  15. Yavari A, Sarkani S, Reddy JN (2001) On nonuniform Euler–Bernoulli and Timoshenko beams with jump discontinuities: application of distribution theory. Int J Solids Struct 38: 8389–8406

    Article  MathSciNet  MATH  Google Scholar 

  16. Biondi B, Caddemi S (2005) Closed form solutions of Euler–Bernoulli beams with singularities. Int J Solids Struct 42: 3027–3044

    Article  MATH  Google Scholar 

  17. Biondi B, Caddemi S (2007) Euler–Bernoulli beams with multiple singularities in the flexural stiffness. Eur J Mech A-Solid 26: 789–809

    Article  MathSciNet  MATH  Google Scholar 

  18. Wang J, Qiao P (2007) Vibration of beams with arbitrary discontinuities and boundary conditions. J Sound Vib 308: 12–27

    Article  Google Scholar 

  19. Batra RC, Porfiri M, Spinello D (2008) Free and forced vibrations of a segmented bar by a meshless local Petrov–Galerkin (MLPG) formulation. Comput Mech 41: 473–491

    Article  MathSciNet  MATH  Google Scholar 

  20. Lu ZR, Huang M, Liu JK, Chen WH, Liao WY (2009) Vibration analysis of multiple-stepped beams with the composite element model. J Sound Vib 322: 1070–1080

    Article  Google Scholar 

  21. Jaworski JW, Dowell EH (2008) Free vibration of a cantilevered beam with multiple steps: Comparison of several theoretical methods with experiment. J Sound Vib 312: 713–725

    Google Scholar 

  22. Papangelis JP, Hancock GJ (1995) Computer analysis of thin-walled structural members. Comput Struct 56: 157–176

    Article  MATH  Google Scholar 

  23. Kapania RK, Castel F (1990) A simple element for aeroelastic analysis of undamaged and damaged wings. AIAA J 28: 329–337

    Article  MATH  Google Scholar 

  24. Dimarogonas AD (1996) Vibration of cracked structures: a state of the art review. Eng Fract Mech 55: 831–857

    Article  Google Scholar 

  25. Surace C, Ruotolo R (1997) Damage assessment of multiple cracked beams: numerical results and experimental validation. J Sound Vib 206: 567–588

    Article  Google Scholar 

  26. Chondros TG, Dimarogonas AD, Yao J (1998) A continuous cracked beam’s vibration theory. J Sound Vib 215: 17–34

    Article  Google Scholar 

  27. Song O, Ha TW, Librescu L (2003) Dynamics of anisotropic composite cantilevers weakened by multiple transverse open cracks. Eng Fract Mech 70: 105–123

    Article  Google Scholar 

  28. Wang K, Inman DJ (2007) Crack-induced effects on aeroelasticity of an unswept composite wing. AIAA J 45: 542–551

    Article  Google Scholar 

  29. Wang K, Inman DJ, Farrar CR (2005) Modeling and analysis of a cracked composite cantilever beam vibrating in coupled bending and torsion. J Sound Vib 284: 23–49

    Article  Google Scholar 

  30. Dang TD, Kapania RK, Patil MJ (2010) Analytical modeling of cracked thin-walled beams under torsion. AIAA J 48: 664–675

    Article  Google Scholar 

  31. Leissa AW (2005) The historical bases of the Rayleigh and Ritz methods. J Sound Vib 287: 961–978

    Article  Google Scholar 

  32. Courant R (1943) Variational methods for the solution of problems of equilibrium and vibrations. Bull Am Math Soc 49: 1–23

    Article  MathSciNet  MATH  Google Scholar 

  33. Cook RD, Malkus DS, Plesha ME, Witt RJ (2002) Concepts and applications of finite element analysis, 4th edn. Wiley, New York

    Google Scholar 

  34. Kumar SYV, Paik JK (2004) Buckling analysis of cracked plates using hierarchical trigonometric functions. Thin Wall Struct 42: 687–700

    Article  Google Scholar 

  35. Beslin O, Nicolas J (1997) A hierarchical functions set for predicting very high order plate bending modes with any boundary conditions. J Sound Vib 202: 633–655

    Article  Google Scholar 

  36. Barrette M, Berry A, Beslin O (2000) Vibration of stiffened plates using hierarchical trigonometric functions. J Sound Vib 235: 727–747

    Article  Google Scholar 

  37. Strang G, Fix G (2008) An analysis of the finite element method. New Edition. Wellesley-Cambridge Press, Massachusetts

    Google Scholar 

  38. Bardell NS (1991) Free vibration analysis of a flat plate using the hierarchical finite element method. J Sound Vib 151: 263–289

    Article  Google Scholar 

  39. Kapania RK, Singhvi S (1992) Efficient free vibration analysis of generally laminated skew plates. Compos Eng 2: 197–212

    Article  Google Scholar 

  40. Singhvi S, Kapania RK (1994) Comparison of simple and Chebychev polynomials in Rayleigh–Ritz analysis. J Eng Mech-ASCE 120: 2126–2135

    Article  Google Scholar 

  41. Gjelsvik A (1981) The theory of thin walled bars. Wiley, New York

    MATH  Google Scholar 

  42. Gunnlaugsson GA, Pedersen PT (1982) A finite element formulation for beams with thin walled cross-sections. Comput Struct 15: 691–699

    Article  MATH  Google Scholar 

  43. Moes N, Dolbow J, Belytschko T (1999) A finite element method for crack growth without meshing. Int J Numer Methods Eng 46: 131–150

    Article  MATH  Google Scholar 

Download references

Author information

Author notes

  1. Thi D. Dang

    Present address: School of Mechanical Engineering, Hanoi University of Science and Technology, Hanoi, Vietnam

Authors and Affiliations

  1. Department of Aerospace and Ocean Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA, 24061-0203, USA

    Thi D. Dang, Rakesh K. Kapania & Mayuresh J. Patil

Authors
  1. Thi D. Dang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rakesh K. Kapania
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mayuresh J. Patil
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Thi D. Dang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dang, T.D., Kapania, R.K. & Patil, M.J. Ritz analysis of discontinuous beams using local trigonometric functions. Comput Mech 47, 235–250 (2011). https://doi.org/10.1007/s00466-010-0540-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-010-0540-y

Keywords

Search

Navigation