Skip to main content
SpringerLink
Log in

Geometric nonlinear analysis of plates and cylindrical shells via a linearly conforming radial point interpolation method

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

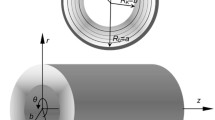
In this paper, the linearly conforming radial point interpolation method is extended for geometric nonlinear analysis of plates and cylindrical shells. The Sander’s nonlinear shell theory is utilized and the arc-length technique is implemented in conjunction with the modified Newton–Raphson method to solve the nonlinear equilibrium equations. The radial and polynomial basis functions are employed to construct the shape functions with Delta function property using a set of arbitrarily distributed nodes in local support domains. Besides the conventional nodal integration, a stabilized conforming nodal integration is applied to restore the conformability and to improve the accuracy of solutions. Small rotations and deformations, as well as finite strains, are assumed for the present formulation. Comparisons of present solutions are made with the results reported in the literature and good agreements are obtained. The numerical examples have demonstrated that the present approach, combined with arc-length method, is quite effective in tracing the load-deflection paths of snap-through and snap-back phenomena in shell problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. MacNeal RH, Harder RL (1985) A proposed standard set of problems to test finite element accuracy. Finite Elem Anal Des 1: 3–20

    Article  Google Scholar 

  2. Belytschko T, Stolarski H, Liu Wk, Carpenter N, Ong JSJ (1985) Stress projection for membrane and shear locking in shell finite elements. Comput Methods Appl Mech Eng 51: 221–258

    Article  MATH  MathSciNet  Google Scholar 

  3. Simo J, Fox DD (1989) On a stress resultant geometrically exact shell model, part I: formulation and optimal parameterization. Comput Methods Appl Mech Eng 72: 267–304

    Article  MATH  MathSciNet  Google Scholar 

  4. Simo J, Fox DD, Rifai MS (1989) On a stress resultant geometrically exact shell model, part II: the linear theory. Comput Methods Appl Mech Eng 73: 53–92

    Article  MATH  MathSciNet  Google Scholar 

  5. Sabir AB, Lock AC (1973) The application of finite elements to the large deflection geometrically nonlinear behaviour of cylindrical shells. In: International conference on variational methods in engineering, Southampton, England, pp 7/67–7/76

  6. Bergan PG, Nygard MK (1985) Nonlinear shell analysis using free formulation finite elements. In: Finite element methods for nonlinear problems, Europe–US Symposium, Tronhelm, Norway

  7. Palazotto AN, Dennis ST (1992) Nonlinear analysis of shell structures. AIAA education series, Wahsington DC

  8. Choi CK, Paik JG (1996) An effective four node degenerated shell element for geometrically nonlinear analysis. Thin-Walled Struct 24: 261–283

    Article  Google Scholar 

  9. Sze KY, Zheng SJ (1999) A hybrid-stress nine-node degenerated shell element for geometrical nonlinear analysis. Comput Mech 23: 448–456

    Article  MATH  Google Scholar 

  10. Sze KY, Chan WK, Pian THH (2002) An eight-node hybrid-stress solid-shell element for geometric nonlinear analysis of elastic shells. Int J Numer Methods Eng 55: 853–878

    Article  MATH  Google Scholar 

  11. Hauptmann R, Schweizerhof K (1998) A systematic development of solid-shell element formulations for linear and nonlinear analyses employing only displacement degrees of freedom. Int J Numer Methods Eng 42: 49–69

    Article  MATH  Google Scholar 

  12. Reddy JN (2004) Mechanics of laminated composite plates and shells: theory and analysis, 2nd edn. CRC Press, Baca Raton

    Google Scholar 

  13. Arciniega RA, Reddy JN (2007) Large deformation analysis of functionally graded shells. Int J Solids Struct 44: 2036–2052

    Article  MATH  Google Scholar 

  14. Krysl P, Belytschko T (1996) Analysis of thin shells by the element-free Galerkin method. Int J Solids Struct 33: 3057–3080

    Article  MATH  Google Scholar 

  15. Noguchi H, Kawashima T, Miyamura T (2000) Element free analyses of shell and spatial structures. Int J Numer Methods Eng 47: 1215–1240

    Article  MATH  Google Scholar 

  16. Li S, Hao W, Liu WK (2000) Numerical simulations of large deformation of thin shell structures using meshfree methods. Comput Mech 25: 102–116

    Article  MATH  Google Scholar 

  17. Wang JG, Liu GR (2002) A point interpolation meshless method based on radial basis functions. Int J Numer Methods Eng 54: 1623–1648

    Article  MATH  Google Scholar 

  18. Liu GR, Gu YT (2001) A point interpolation method for two-dimensional solids. Int J Numer Methods Eng 50: 937–951

    Article  MATH  Google Scholar 

  19. Liu GR, Dai KY, Lim KM, Gu YT (2003) A radial point interpolation method for simulation of two-dimensional piezoelectric structures. Smart Mater Struct 12: 171–180

    Article  Google Scholar 

  20. Zhang GY, Liu GR, Wang YY, Huang HT, Zhong ZH, Li GY, Han X (2007) A linearly conforming point interpolation method (LC-PIM) for three-dimensional elasticity problems. Int J Numer Methods Eng 72: 1524–1543

    Article  MathSciNet  Google Scholar 

  21. Liu GR, Li Y, Dai KY, Luan MT, Xue W (2006) A linearly conforming RPIM for solids mechanics problems. Int J Comput Methods 3: 401–428

    Article  MathSciNet  Google Scholar 

  22. Beissel S, Belytschko T (1996) Nodal integration of the element-free Galerkin method. Comput Methods Appl Mech Eng 139: 49–74

    Article  MATH  MathSciNet  Google Scholar 

  23. Bonet J, Kulasegaram S (1999) Correction and stabilization of smoothed particle hydrodynamics methods with applications in metal forming simulations. Int J Numer Methods Eng 47: 1189–1214

    Article  Google Scholar 

  24. Chen JS, Wu CT, Yoon S, You Y (2001) A stabilized conforming nodal integration for Galerkin mesh-free methods. Int J Numer Methods Eng 50: 435–466

    Article  MATH  Google Scholar 

  25. Crisfield MA (1997) Non-linear finite element analysis of solids and structures, vol 2. Wiley, Chichester

    Google Scholar 

  26. Sze KY, Chen JS, Sheng N, Liu XH (2004) Stabilized conforming nodal integration: exactness and variational justification. Fin Elem Anal Des 41: 147–171

    Article  Google Scholar 

  27. Sanders JL Jr (1963) Nonlinear theories for thin shells. Q Appl Math 21: 21–36

    MathSciNet  Google Scholar 

  28. Flügge W (1973) Stresses in shells, 2nd edn. Springer, Berlin

    Google Scholar 

  29. Sze KY, Liu XH, Lo SH (2004) Popular benchmark problems for geometric nonlinear analysis of shells. Fin Elem Anal Des 40: 1551–1569

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Centre for Advanced Computations in Engineering Science (ACES), Department of Mechanical Engineering, The National University of Singapore, 9 Engineering Drive 1, Singapore, 117576, Singapore

    X. Zhao, G. R. Liu & K. Y. Dai

  2. The Singapore-MIT Alliance (SMA), E4-04-10, 4 Engineering Drive 3, Singapore, 117576, Singapore

    G. R. Liu

  3. Key Laboratory of Advanced Technology for Vehicle Body Design and Manufacture, M.O.E, Hunan University, Changsha, 410082, People’s Republic of China

    Z. H. Zhong, G. Y. Li & X. Han

Authors
  1. X. Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. R. Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. Y. Dai
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Z. H. Zhong
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. G. Y. Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. X. Han
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to X. Zhao.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhao, X., Liu, G.R., Dai, K.Y. et al. Geometric nonlinear analysis of plates and cylindrical shells via a linearly conforming radial point interpolation method. Comput Mech 42, 133–144 (2008). https://doi.org/10.1007/s00466-008-0242-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-008-0242-x

Keywords

Search

Navigation