Skip to main content
SpringerLink
Log in

Mixed state-vector finite element analysis for a higher-order box beam theory

  • Published:
Computational Mechanics Aims and scope Submit manuscript

Abstract

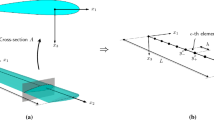
If thin-walled closed beams are analyzed by the standard Timoshenko beam elements, their structural behavior, especially near boundaries, cannot be accurately predicted because of the incapability of the Timoskenko theory to predict the sectional warping and distortional deformations. If a higher-order thin-walled box beam theory is used, on the other hand, accurate results comparable to those obtained by plate finite elements can be obtained. However, currently available two-node displacement based higher-order beam elements are not efficient in capturing exponential solution behavior near boundaries. Based on this motivation, we consider developing higher-order mixed finite elements. Instead of using the standard mixed formulation, we propose to develop the mixed formulation based on the state-vector form so that only the field variables that can be prescribed on the boundary are interpolated for finite element analysis. By this formulation, less field variables are used than by the standard mixed formulation, and the interpolated field variables have the physical meaning as the boundary work conjugates. To facilitate the discretization, two-node elements are considered. The effects of interpolation orders for the generalized stresses and displacements on the solution behavior are investigated along with numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Vlasov VZ (1961) Thin walled elastic beams. Israel Program for Scientific Translations, Jerusalem

  • Steinle A (1970) Torsion und profilverformung beim einzelligen Kastentrer, Beton- und Stahlbetonbau, Heft 9:215–222

    Google Scholar 

  • Maisel BI, Roll F (1974) Methods of analytical and design of concrete box beams with side cantilevers. Technical Report, Cement and Concrete Association, London

  • Maisel BI (1982) Analysis of concrete box beams using small-computer capacity. Development Report 5, Cement and Concrete Association, London.

  • Boswell LF, Zhang SH (1983) A box beam finite element for the elastic analysis of thin-walled structures. Thin-Walled Structures 1:353–383

    Google Scholar 

  • Boswell LF, Zhang SH (1984) The effect of distortion in thin-walled box-spine beams. Int J Solids and Structures 20(9):845–862

    Google Scholar 

  • Schardt R (1990) Die verallgemeinerte technische biegetheorie, Springer Verlag, Berlin, Heidelberg, New York

  • Balch CD, Steele CR (1987) Asymptotic solutions for warping and distortion of thin-walled box beams. ASME J Appl Mech 54:165–173

    Google Scholar 

  • Hsu YT, Fu SS, Schelling DR (1995) EBEF method for distortional analysis of steel box girder bridges. J Struct Div ASCE 121(3):557–566

    Google Scholar 

  • Jönsson J (1999) Distortional warping functions and shear distributions in thin-walled beams. Thin-Walled Struct. 33:245–268

    Google Scholar 

  • Razaqpur AG , Li H (1991) Thin-walled multicell box-girder finite element. J Struc Eng ASCE 117(10):2953–2971

    Google Scholar 

  • Razaqpur AG, Li H (1994) Refined analysis of curved thin-walled multicell box-girders. Comput Struct 53(1):131–142

    Google Scholar 

  • Kim JH, Kim YY (1999) Analysis of thin-walled closed beams with general quadrilateral cross sections. ASME J Appl Mech 66:904–912

    Google Scholar 

  • Kim JH, Kim YY (2001) Thin-walled multi-cell beam analysis for coupled torsion, distortion and warping deformations. ASME J Appl Mech 68:260–269

    Google Scholar 

  • Hellinger E (1914) Die allgemeine aussetze der mechanik der kontinua. in Encyclopedia der Matematischen Wissenschaften 4 (eds Klein F and Muller C), Tebner, Leipzig

  • Reissner E (1950) On a variational theorem in elasticity. J Math Phys 29:90–95

    Google Scholar 

  • Steele CR, Kim YY (1992) Modified mixed variational principle and the state-vector equation for elastic bodies and shells of revolution. ASME J Appl Mech 59:587–595

    Google Scholar 

  • Washizu K (1982) Variational methods in elasticity and plasticity. Pergamon Press, Oxford

  • Prathap G (1993) The finite element method in structural mechanics. Kluwer Academic Publishers

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Kunsan National University, Kunsan, Chonbuk, 573-701, Korea

    G.-W. Jang

  2. School of Mechanical and Aerospace Engineering and National Creative Research Initiatives Center for Multiscale Design, Seoul National University, Seoul, 151-742, Korea

    Y. Y. Kim

Authors
  1. G.-W. Jang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Y. Y. Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Y. Y. Kim.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jang, GW., Kim, Y. Mixed state-vector finite element analysis for a higher-order box beam theory. Comput Mech 36, 217–225 (2005). https://doi.org/10.1007/s00466-004-0656-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-004-0656-z

Keywords

Search

Navigation