Connectivity and $W_v$-Paths in Polyhedral Maps on Surfaces

Abstract

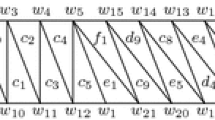
The $W_v$-path conjecture due to Klee and Wolfe states that any two vertices of a simple polytope can be joined by a path that does not revisit any facet. This is equivalent to the well-known Hirsch conjecture. Klee proved that the $W_v$-path conjecture is true for all 3-polytopes (3-connected plane graphs), and conjectured even more, namely that the $W_v$-path conjecture is true for all general cell complexes. This general $W_v$-path conjecture was verified for polyhedral maps on the projective plane and the torus by Barnette, and on the Klein bottle by Pulapaka and Vince. Let G be a graph polyhedrally embedded in a surface $\Sigma$, and x, y be two vertices of G. In this paper, we show that if there are three internally disjoint (x, y)-paths which are homotopic to each other, then there exists a $W_v$-path joining x and y. For every surface $\Sigma$, define a function $f(\Sigma )$ such that if for every graph polyhedrally embedded in $\Sigma$ and for a pair of vertices x and y in V(G), the local connectivity $\kappa _G(x,y) \ge f(\Sigma )$, then there exists a $W_v$-path joining x and y. We show that $f(\Sigma )=3$ if $\Sigma$ is the sphere, and for all other surfaces $3-\tau (\Sigma )\le f(\Sigma )\le 9-4\chi (\Sigma )$, where $\chi (\Sigma )$ is the Euler characteristic of $\Sigma$, and $\tau (\Sigma )=\chi (\Sigma )$ if $\chi (\Sigma )< -1$ and 0 otherwise. Further, if x and y are not cofacial, we prove that G has at least $\kappa _G(x,y)+4\chi (\Sigma )-8$ internally disjoint $W_v$-paths joining x and y. This bound is sharp for the sphere. Our results indicate that the $W_v$-path problem is related to both the local connectivity $\kappa _G(x,y)$, and the number of different homotopy classes of internally disjoint (x, y)-paths as well as the number of internally disjoint (x, y)-paths in each homotopy class.