Abstract
We give the first efficient (1−ε)-approximation algorithm for the following problem: Given an axis-parallel d-dimensional box R in ℝd containing n points, compute a maximum-volume empty axis-parallel d-dimensional box contained in R. The minimum of this quantity over all such point sets is of the order \(\Theta (\frac {1}{n} )\). Our algorithm finds an empty axis-aligned box whose volume is at least (1−ε) of the maximum in O((8edε −2)d⋅nlogd n) time. No previous efficient exact or approximation algorithms were known for this problem for d≥4. As the problem has been recently shown to be NP-hard in arbitrarily high dimensions (i.e., when d is part of the input), the existence of an efficient exact algorithm is unlikely.
We also present a (1−ε)-approximation algorithm that, given an axis-parallel d-dimensional cube R in ℝd containing n points, computes a maximum-volume empty axis-parallel hypercube contained in R. The minimum of this quantity over all such point sets is also shown to be of the order \(\Theta (\frac{1}{n} )\). A faster (1−ε)-approximation algorithm, with a milder dependence on d in the running time, is obtained in this case.


Similar content being viewed by others
Notes
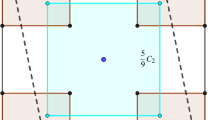
Let ℓ(v) and ℓ′(v) denote the two orthogonal lines incident to a vertex v of U. It is easy to see that there exists a vertex v of U such that when ℓ(v) and ℓ′(v) are translated towards the interior of the square, they hit two distinct points out of the six contained in U. By balancing the areas of the two rectangles swept by these two lines, say R 1 and R 2, with the area of the largest empty sub-rectangle inside the rectangle U∖(R 1∪R 2) as guaranteed by Lemma 2 and Observation 1, we get that A(6)≥x, where \(x=3 -2\sqrt{2}\) is the solution of the quadratic equation x=(1−x)2/4.
The argument we use here is similar to that used for bounding the geometric discrepancy of the van der Corput set of points.
For d=2 volume is replaced by area throughout this proof.
References
Aggarwal, A., Suri, S.: Fast algorithms for computing the largest empty rectangle. In: Proceedings of the 3rd Annual Symposium on Computational Geometry, pp. 278–290 (1987)
Atallah, M., Fredrickson, G.: A note on finding the maximum empty rectangle. Discrete Appl. Math. 13, 87–91 (1986)
Atallah, M., Kosaraju, S.R.: An efficient algorithm for maxdominance, with applications. Algorithmica 4, 221–236 (1989)
Beck, J., Chen, W.: Irregularities of Distribution. Cambridge University Press, Cambridge (1987)
Backer, J., Keil, M.: The bichromatic rectangle problem in high dimensions. In: Proceedings of the 21st Canadian Conference on Computational Geometry, pp. 157–160 (2009)
Backer, J., Keil, M.: The mono- and bichromatic empty rectangle and square problems in all dimensions. In: Proceedings of the 9th Latin American Symposium on Theoretical Informatics, pp. 14–25 (2010)
Chazelle, B.: The Discrepancy Method: Randomness and Complexity. Cambridge University Press, Cambridge (2000)
Chazelle, B., Drysdale, R., Lee, D.T.: Computing the largest empty rectangle. SIAM J. Comput. 15, 300–315 (1986)
Chen, W.: Lectures on irregularities of point distribution, web edition. http://rutherglen.ics.mq.edu.au/wchen/researchfolder/iod00.pdf (2000)
Datta, A.: Efficient algorithms for the largest empty rectangle problem. Inf. Sci. 64, 121–141 (1992)
Datta, A., Soundaralakshmi, S.: An efficient algorithm for computing the maximum empty rectangle in three dimensions. Inf. Sci. 128, 43–65 (2000)
Dumitrescu, A., Jiang, M.: On the largest empty axis-parallel box amidst n points. arXiv:0909.3127v2 (2009)
Edmonds, J., Gryz, J., Liang, D., Miller, R.: Mining for empty spaces in large data sets. Theor. Comput. Sci. 296(3), 435–452 (2003)
Halton, J.H.: On the efficiency of certain quasi-random sequences of points in evaluating multi-dimensional integrals. Numer. Math. 2, 84–90 (1960)
Hammersley, J.M.: Monte Carlo methods for solving multivariable problems. Ann. N.Y. Acad. Sci. 86, 844–874 (1960)
Matoušek, J.: Geometric Discrepancy: An Illustrated Guide. Springer, Berlin (1999)
McKenna, M., O’Rourke, J., Suri, S.: Finding the largest rectangle in an orthogonal polygon. In: Proceedings of the 23rd Annual Allerton Conference on Communication, Control and Computing, Urbana-Champaign, Illinois, October 1985
Namaad, A., Lee, D.T., Hsu, W.-L.: On the maximum empty rectangle problem. Discrete Appl. Math. 8, 267–277 (1984)
Orlowski, M.: A new algorithm for the largest empty rectangle problem. Algorithmica 5, 65–73 (1990)
Rote, G., Tichy, R.F.: Quasi-Monte-Carlo methods and the dispersion of point sequences. Math. Comput. Model. 23, 9–23 (1996)
Ruiz, S.M.: A result on prime numbers. Math. Gaz. 81, 269–270 (1997)
Smid, M.: Closest-point problems in computational geometry. In: Sack, J.-R., Urrutia, J. (eds.) Handbook of Computational Geometry, pp. 877–932. North-Holland, Amsterdam (1999)
Srinivasan, S.: On two-dimensional Hammersley’s sequences. J. Number Theory 10, 421–429 (1978)
Tucker, A.: Applied Combinatorics, 3rd edn. Wiley, New York (1995)
van der Corput, J.G.: Verteilungsfunktionen I. Proc. K. Ned. Akad. Wet. 38, 813–821 (1935)
van der Corput, J.G.: Verteilungsfunktionen II. Proc. K. Ned. Akad. Wet. 38, 1058–1066 (1935)
Acknowledgement
The authors would like to thank the anonymous reviewers for careful reading and thoughtful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
A. Dumitrescu was supported in part by NSF CAREER grant CCF-0444188 and NSF grant DMS-1001667. Part of the research by this author was done at Ecole Polytechnique Fédérale de Lausanne.
M. Jiang was supported in part by NSF grant DBI-0743670.
Rights and permissions
About this article
Cite this article
Dumitrescu, A., Jiang, M. On the Largest Empty Axis-Parallel Box Amidst n Points. Algorithmica 66, 225–248 (2013). https://doi.org/10.1007/s00453-012-9635-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00453-012-9635-5