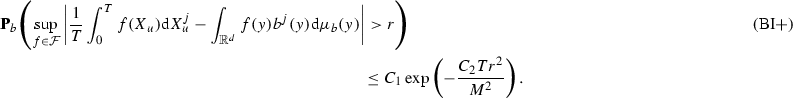Abstract
The problem of pointwise adaptive estimation of the drift coefficient of a multivariate diffusion process is investigated. We propose an estimator which is sharp adaptive on scales of Sobolev smoothness classes. The analysis of the exact risk asymptotics allows to identify the impact of the dimension and other influencing values—such as the geometry of the diffusion coefficient—of the prototypical drift estimation problem for a large class of multidimensional diffusion processes. We further sketch generalizations of our results to arbitrary diffusions satisfying suitable Bernstein-type inequalities.
Similar content being viewed by others
1 Introduction and motivation
Diffusions present a particularly important class of stochastic processes. The long standing probabilistic interest in this subject is illustrated, for example, by the seminal books of Itō and McKean [9] and Stroock and Varadhan [22]. From the statistical point of view, one classical problem is to estimate the (unknown) characteristics of the diffusion, both from continuous-time and discrete observations. In the last two decades, nonparametric estimation of diffusion processes has been widely developed, mainly due to their applications in mathematical finance where diffusions are commonly used to model the evolution of financial assets or portfolios of assets. While diffusion models have been largely univariate in the past, they now predominantly include multiple state variables; see the introductory remarks of Aït-Sahalia [1] for concrete examples. In some respects, the statistical theory did not keep pace with this evolution: thorough theoretical results on nonparametric estimation of multidimensional diffusion processes are few and far between. At least partially, this is due to the fact that the concept of diffusion local time and related tools such as the occupation times formula are not available in dimension \(d >1\) such that the treatment of the multivariate case requires different approaches and new techniques.
The aim of this paper is to close one gap in the literature by analyzing the asymptotically exact behavior of the pointwise risk for adaptively estimating the drift vector \(b: \mathbb {R}^d \rightarrow \mathbb {R}^d\) of a multivariate diffusion which is given as a solution of the stochastic differential equation
where \(\sigma : \mathbb {R}^d \rightarrow \mathbb {R}^{d\times d}\) is the dispersion matrix, \(W\) is a \(d\)-dimensional standard Wiener process and the initial value \(\xi \in \mathbb {R}^d\) is independent of \(W\). It will be assumed throughout that a continuous record of observations \(X^T := (X_t)_{0\le t \le T}\) is available. Thus, the diffusion coefficient \(\sigma \sigma ^\top \) is identifiable by means of the semimartingale quadratic variation, and it means only little loss of generality to simplify the analysis by considering merely the case of known, constant diffusion part. We further restrict attention to ergodic diffusions whose invariant measure is absolutely continuous with respect to the Lebesgue measure. Let \(\rho _{b}\) denote the invariant density. The initial value \(\xi \) is assumed to follow the invariant law such that the process \(X\) is strictly stationary.
It is statistical folklore to consider drift estimation as some analogue of the regression problem. Given some appropriately chosen kernel \(K: \mathbb {R}^d \rightarrow \mathbb {R}\) and bandwidth \(h>0\), it thus appears natural to investigate the following type of kernel estimators of the drift vector \(b\),
where \(K_h(\cdot ) := h^{-d}K(\cdot /h)\), \(\widehat{\rho }_T\) is some estimator of the invariant density \(\rho _{b}\) and \(\rho _*(x)>0\) denotes some a priori lower bound on \(\rho _{b}(x)\). In the sequel, the quality of an estimator \(\widehat{b}_T\) will be quantified by its pointwise risk
for \(\mathbf {E}_b\) denoting expectation with respect to the invariant measure associated with \(b\) and \(\Vert \cdot \Vert \) denoting the Euclidean norm. The goal is to define minimax adaptive estimators \(b_T^*\) satisfying
The supremum here extends over a given class of functions \({\fancyscript{B}}\), typically, a class of functions satisfying certain smoothness assumptions or structural constraints. For estimating the drift vector, we shall consider scales of Sobolev classes \((\varSigma _T(\beta ,L))_{(\beta ,L)\in {\mathcal {B}}_T}\) where, for fixed \(\beta _*>d/2\) and \(0<L_*<L^*<\infty \),
We propose estimators which attain not only the optimal rate of convergence but the best exact asymptotic minimax risk when the actual smoothness of the drift and the associated invariant density \(\rho _b\) are unidentified and we only assume membership to \(\varSigma _T(\beta ,L)\) for some \((\beta ,L)\in \mathcal {B}_T\).
To the best of our knowledge, sharp asymptotic minimax bounds for nonparametric estimation in the diffusion framework have been established exclusively for one-dimensional processes up to now. One particularly deep result is given in Dalalyan [5] where a fully data-driven procedure for exact global estimation of the drift for a large class of ergodic scalar diffusion processes is proven. In the multidimensional diffusion set-up however, we only know of upper bound results on rates of convergence, even for the prototypical problem of estimating the drift vector from continuous-time observations. Let us emphasize that the question of identifying the exact constant in the risk asymptotics is far from being merely of theoretical interest. The subsequent in-depth analysis rather allows to descry the influencing values of the drift estimation problem, and these findings provide answers to practice-oriented issues. For instance, it is to be expected—and has been observed in practice indeed—that the speed of convergence for estimating functionals of a diffusion process solution of the SDE (1.1) depends on the geometry of the diffusion coefficient \(\sigma \sigma ^\top =: a=(a_{jk})_{1\le j,k\le d}\). For the exemplary problem of estimating the \(j\)-th component \(b^j\) of the drift vector, \(j\in \{1,\ldots ,d\}\) fixed, the dependence will be proven to be reflected by the appearance of \(a_{jj}\), the \(j\)-th diagonal entry of the diffusion matrix, in the exact normalizing factor in the risk asymptotics. Our exact results further give a theoretical justification for the wide-spread use of standard kernel methods for drift estimation which in applications (e.g., in financial econometrics) often occurs on an ad-hoc basis. Heuristically, the use of such methods is based on the aforementioned folklore that “drift estimation is just regression,” provided that the long observation limit is considered and as long as the diffusion is sufficiently regular.
On a mathematically formal level, abstract decision theory allows to transfer risk bounds from one statistical model to another by referring to the concept of asymptotic equivalence of experiments in the sense of Le Cam. For inference on the drift in multidimensional ergodic diffusion models, asymptotic equivalence is established in Dalalyan and Reiß [7]. Their results concern the special case of Kolmogorov diffusions with unit diffusion part, i.e. \(\sigma = \mathbf {Id}\), and hold only for large enough Hölder smoothness of the drift coefficient (which is substantially larger than the lower bound of \(d/2\) which would correspond to known results on asymptotic nonequivalence of scalar nonparametric experiments when the smoothness index is \(1/2\)). We take a direct approach and establish upper and lower asymptotic risk bounds for diffusions with general constant and nondegenerate diffusion part without resorting to arguments based on asymptotic equivalence.
For ease of presentation however, let us merely announce the result for the important special case of diffusions with dispersion matrix of the form \(\sigma =\sigma _0~\mathbf {Id}\), for some \(0\ne \sigma _0\in \mathbb {R}\). Define
Here, with \(B(\cdot ,\cdot )\) and \(\varGamma (\cdot )\) denoting the Beta and the Gamma function, respectively, and letting \(\mathbb {S}_d:=2\pi ^{d/2}/\varGamma (d/2)\) denote the surface of the unit sphere in \(\mathbb {R}^d\),
On the one hand, we show that
for some suitably defined functional sets \(\varPi (c_1,c_2)\) and \(\varSigma _T(\beta ,L)=\Sigma _T(\beta ,L;L',\sigma _0)\), depending also on \(\sigma _0\) and constants \(c_1,c_2,L'\) related to the regularity properties of the class of investigated multivariate diffusion processes (for details, see Sects. 2 and 5). Furthermore, we suggest an asymptotically sharp adaptive estimator over \({\mathcal {B}}_T\), i.e. an adaptive estimator which does not only achieve the best possible rate of convergence but the best asymptotic constant associated to it. Our exact asymptotic results on drift estimation hold under mild regularity constraints and indicate that asymptotic equivalence—at least in some reduced sense—also holds under smoothness assumptions less severe than those imposed in Dalalyan and Reiß [7]; cf. the discussion in Sect. 6.
The current investigation is directly related to previous work both from the field of nonparametric statistics and more applied areas such as financial econometrics. A larger quantity of results on nonparametric drift estimation in the scalar diffusion case is already available. Dalalyan and Kutoyants [6] consider the problem of nonparametric estimation of the derivative of the invariant density and of the drift coefficient for scalar ergodic diffusion processes over weighted \(L^2\) Sobolev classes. The construction of the suggested asymptotically efficient estimator requires the knowledge of the smoothness and the radius of these weighted Sobolev balls. On the basis of these results, Dalalyan [5] develops an adaptive procedure which does not depend on the characteristics of the Sobolev ball and which is asymptotically minimax simultaneously over a broad scale of Sobolev classes. In direct relation to the present work, Spokoiny [20] considers the problem of pointwise adaptive drift estimation and develops a locally linear smoother with data-driven bandwidth choice. His method is also derived in a scalar setting but generalizes to the multidimensional framework. The focus of Spokoiny [20] clearly differs from ours: he provides nonasymptotic results (which do not require stationarity, ergodicity or mixing properties of the observed diffusion process) for the suggested kernel type estimators, while our interest is in identifying the asymptotically exact behavior of adaptive drift estimators. The definition of such asymptotically sharp adaptive estimators does not only require a data-dependent choice of the smoothing parameter but also a data-driven selection of the kernel.
In the sequel, we will use rather recent results on functional inequalities (and the interplay of different types thereof) for diffusion processes. To be more precise, inspection of the constructive proof of the asymptotic upper risk bound suggests that the combination of a Bernstein-type deviation inequality and sufficiently tight variance bounds is the key for suggesting sharp adaptive drift estimation procedures for diffusion processes. Diverse works on generalizations of the classical Bernstein inequality which are applicable in the diffusion framework exist. In this paper, we will assume that the diffusion satisfies the spectral gap inequality—a condition which, at least in the area of statistics for random processes, is rather unconventional. However, it can be argued that this hypothesis presents some sort of minimal assumption for a Bernstein-type inequality for symmetric diffusion processes to hold and thus provides a natural framework for our investigation. The combination of different types of tail estimates of additive functionals and sharp variance bounds due to Dalalyan and Reiß [7] then allows to prove the required type of exponential inequalities, and classical chaining arguments and conditions on the size of function classes in terms of bracketing numbers provide an extension to uniform versions thereof. Our results still are by no means restricted to this specific kind of dependence mechanism as will be sketched later. Currently, (probabilistic) research on diffusion processes is aimed at investigating the interplay between different approaches for the study of quantitative ergodic properties and the relationship between different functional inequalities. It would be interesting to complement these results with findings on the asymptotic statistical behavior of estimators in the respective ergodic diffusion models, and the present analysis provides one first step in this direction.
Outline of the paper One crucial point in our subsequent investigation is the fact that we may restrict attention to analyzing the exact asymptotics of the estimators which appear in the numerator of (1.2). Only mild regularity properties of the diffusion are required for translating results on estimating
into upper and lower bounds for drift estimation. We thus start our investigation with considering estimation of \(b\rho _{b}\), assuming that the components \(b^j\rho _{b}\), \(j\in \{1,\ldots ,d\}\), belong to some Sobolev class of regularity \(\beta \in {\mathcal {I}}\), \({\mathcal {I}}\) some given interval of the form \(\big [\beta _*,\beta _T\big ]\) with \(\beta _T \rightarrow _{T\rightarrow \infty }\infty \) slowly enough. Section 3 contains a lower bound for pointwise estimation of \(b\rho _{b}\), and an adaptive procedure for estimating the components of \(b\rho _{b}\) which asymptotically attains the respective infimum is introduced in Sect. 4. Provided that the drift grows at most linearly and the invariant density decays exponentially, upper and lower bounds for estimating \(b\rho _{b}\) can be translated into corresponding results for drift estimation. In favor of a concise and transparent presentation, the bounds are stated explicitly only for Kolmogorov diffusions. The respective results are given in Sect. 5. Section 6 contains a discussion of our findings and a sketch of possible extensions. Details on the exponential inequality used in the proof of the upper bound part of our exact result are given in Appendix A. The bulk of the proofs of the main results is deferred to Appendix B.
General definitions and notation For \(g:\mathbb {R}^d \rightarrow \mathbb {R}^d\), denote by \(g^j\) its \(j\)-th component. For a smooth function \(f: \mathbb {R}^d \rightarrow \mathbb {R}\), let \(\partial _j f:= \partial f/\partial x^j\), and denote its gradient by \(\nabla f = (\partial _j f)_j\). Rows of an \(d\times d\)-matrix \(a\) are denoted by \(a_j\), and the Frobenius norm of the matrix \(\sigma \) is denoted by \(\Vert \sigma \Vert _{S_2} := (\sum _{j=1}^d (\sigma \sigma ^\top )_{jj})^{1/2}\). Let \(\phi _f\) be the Fourier transform of \(f \in L^2(\mathbb {R}^d)\), that is, for any \(\lambda \in \mathbb {R}^d\), \(\phi _f(\lambda ) := \int _{\mathbb {R}^d}f(x)\exp (\mathrm{i } \lambda ^\top x)\mathrm {d}x\). Let \(\beta >d/2\), and define the Sobolev seminorm \(\eta _\beta (\cdot )\) by
The isotropic Sobolev class \({\mathcal {S}}(\beta ,L)\) is given as \({\mathcal {S}}(\beta ,L) \!:=\! \left\{ f \!\in \! L^2(\mathbb {R}^d): \eta _{\beta }(f)\!\le \! L\right\} \). Throughout, \(\lesssim \) means less or equal up to some constant which does not depend on the variable parameters in the expression.
2 Preliminaries
The complexity of the diffusion model requires some care in defining the framework for pointwise estimation of the components of the drift vector, with special consideration of the interplay of regularity properties of the individual components of the model. We start by defining \(\varPi _0=\varPi _0(\sigma )\), \(\sigma \) some constant nondegenerate \(\mathbb {R}^{d\times d}\)-valued dispersion matrix with associated diffusion coefficient \(\sigma \sigma ^\top =a\), as the set of all drift coefficients \(b:\mathbb {R}^d\rightarrow \mathbb {R}^d\) such that
- (\(\hbox {P}_0\)):
-
the SDE
$$\begin{aligned} \mathrm {d}X_t = b(X_t)\mathrm {d}t +\sigma ~ \mathrm {d}W_t \end{aligned}$$(2.1)admits a strong solution which is ergodic with Lebesgue continuous invariant measure \(\mathrm {d}\mu _b(x) = \rho _{b}(x)\mathrm {d}x\), and
- (\(\hbox {P}_0'\)):
-
for \(j\in \{1,\ldots ,d\}\), the invariant density \(\rho _{b}\) satisfies the relation
$$\begin{aligned} 2b^j\rho _{b} = a_j\nabla \rho _{b} = \sum _{k=1}^d a_{jk} \partial _k\rho _{b}. \end{aligned}$$
We further suppose that the initial value \(X_0\) has the density \(\rho _b\) such that \((X_t)_{t\ge 0}\) is strictly stationary.
As aforementioned, the drift estimation problem in the sequel will be decomposed into the individual questions of estimating the invariant density \(\rho _b\) and the products \(b^j\rho _b\), \(j=1,\ldots ,d\). Restricting to diffusion processes satisfying \((\hbox {P}_0')\), the second question can also be stated as estimating the weighted sums of derivatives \(\sum _{k=1}^d a_{jk}\partial _k \rho _b\), \(j=1,\ldots ,d\). As has been proved in Dalalyan and Kutoyants [6] and Dalalyan [5] in the scalar set-up, this approach has the potential to derive deep results. We already noted that the non-existence of diffusion local time presents a particular challenge for the statistical analysis of estimators in the multivariate diffusion framework as a set of valuable technical tools falls away. One further difficulty consists in identifying regularity conditions on the diffusion which allow for an as broad as possible extension of the investigation to a multivariate framework. It is convenient to include the condition \((\mathrm{P }_0')\), but our results can also be generalized to more general classes of diffusion processes.
In the sequel, we consider estimation of the drift function at a point \(x_0\in \mathbb {R}^d\) under Sobolev smoothness constraints on the associated invariant density. Precisely, set
where \(\rho _{T}^*\) is a sequence of positive real numbers such that \(\lim _{T\rightarrow \infty }\rho _{T}^*=0\) and \(\liminf _{T\rightarrow \infty }\left( \rho _T^*\log T\right) >0\). To shorten notation, we frequently write \(\varSigma _T(\beta ,L)\) for \(\varSigma _T(\beta ,L;L',\sigma )\). For constants \(c_1\in (0,\infty ]\) and \(c_2>0\), we further define \(\varPi (c_1,c_2)=\varPi (c_1,c_2,\sigma )\) as the set of all drift functions \(b\in \varPi _0(\sigma )\) satisfying the following conditions:
- \(\mathrm{(P_1) }\) :
-
It holds \(\limsup _{\Vert x\Vert \rightarrow \infty }\Vert x\Vert ^{-2}\left\langle b(x),x\right\rangle = - c_1\).
- \(\mathrm{(P_2) }\) :
-
For all \(x \in \mathbb {R}^d\), we have \(\left\| b(x)\right\| \le c_2(1+\Vert x\Vert )\).
A few comments on the definition of the functional sets \(\Pi _0(\sigma )\) and \(\Pi (c_1,c_2,\sigma )\) are in order:
Remark 1
-
A lower bound on the value \(\rho _b(x_0)\) is required for two reasons: First (and analogously to the case of nonparametric density estimation from i.i.d. observations considered in Butucea [3]), in order to obtain a reasonably good adaptive estimator of the value \((b^j\rho _b)(x_0)\), we have to exclude the case of a density \(\rho _b\) that varies with \(T\) such that \(\rho _b(x_0)\rightarrow 0\) too fast. Secondly, for defining a ratio-type drift estimator in the spirit of (1.2), a strictly positive a priori lower bound \(\rho _*(x_0)<\rho _b(x_0)\) is needed. The regularity conditions on the drift used in the proof of the asymptotic properties of our adaptive estimators actually allow for the derivation of explicit lower bounds; see Remark 2 below.
-
The assumption of ergodicity is central for our subsequent analysis. Existence and uniqueness of invariant measures are conveniently proven by means of versions of Khasminskii’s criterion, involving Lyapunov-type functions for the generator of the diffusion. Assumption \(\mathrm{(P_1) }\) is a radial assumption on the drift coefficient and states that (if \(c_1<\infty \)) the inward radial component of \(b\) has a prescribed polynomial behavior. In particular, \(\mathrm{(P_1) }\) implies that \(\exp (\delta \Vert x\Vert ^2)\) for \(\Vert x\Vert \ge 1\) is a Lyapunov function for small enough \(\delta \), thus ensuring the existence of an invariant measure. Together with the “at most linear growth”-condition in \(\mathrm{(P_2) }\), it further implies an exponential bound on the associated invariant density (see Lemma 1 below).
3 Lower bound for pointwise estimation
In the Gaussian white noise framework, it has been shown by Lepski [12] that estimators which are optimally rate adaptive with respect to the pointwise risk over the scale of Hölder classes do not exist. The best adaptive estimators are proven to achieve only a rate which is slower than the optimal one in a logarithmic factor. Tsybakov [23] derives an analogous result for adaptation over the scale of Sobolev classes. To some extent, our findings are analogous, and principal ideas of the proof basically rely on techniques developed in the classical framework. The exact analysis of the drift estimation problem however also involves some subtleties which go beyond the known intricacies associated to the question of pointwise adaptation.
Let us first state the exact lower bound for estimating the components of \(b\rho _{b}\) adaptively, assuming that the components \(b^j\rho _b \in {\mathcal {S}}(\beta ,L)\), \(j=1,\ldots ,d\), for some \(\beta \in [\beta _*,\infty )\) and \(L \in [L_*,L^*]\). Here, \(\beta _*\in (d/2,\infty )\) and \(0<L_*<L^*<\infty \) are fixed values. For any \(\beta >d/2\), let
and recall the definition of \(\mathbb {I}_\beta \) according to (1.4).
Theorem 1
Fix \(\beta _*>d/2\) and \(\delta \in (0,1)\), and denote \({\mathcal {B}}_T := \left[ \beta _*,\beta _T\right] \times \left[ L_*,L^*\right] \), for \(\beta _T := (\log \log T)^\delta \). Then, for any \(x_0\in \mathbb {R}^d\) and \(j\in \{1,\ldots ,d\}\) fixed,
where the infimum is taken over all estimators \(\widehat{g}_T\) of \(b^j\rho _{b}\) and
The proof of Theorem 1 is deferred to Appendix B.1.
The basic—and classical—idea of the proof of Theorem 1 is to reduce the proof of the lower bound in (3.2) to proving a lower bound on the risk of two suitably chosen hypotheses. A lower bound on the latter risk is then deduced by means of Theorem 6(i) in Tsybakov [23] as it was also done in Butucea [3] and Klemelä and Tsybakov [10, 11]. The verification of the conditions of Tsybakov [23]’s result in the current diffusion framework however requires tools which differ from those used in the references mentioned above. Denoting by \({\mathbb {P}}_0\) and \({\mathbb {P}}_1\) the probability measures associated to the two different hypotheses, it needs to be shown that, for some fixed \(\tau \) and for any \(\alpha \in (0,1/2)\),
In the Gaussian white noise framework considered in Klemelä and Tsybakov [10, 11], (3.4) is verified directly for suitably chosen hypotheses due to the Gaussian nature of the model. For nonparametric density estimation from i.i.d. observations, Butucea [3] uses Lyapunov’s CLT. In our framework, the condition (3.4) is verified by means of the martingale CLT.
4 Construction of sharp adaptive estimators
To define pointwise adaptive estimators of the components of \(b\rho _{b}\) which attain the lower bound established in the previous section, we act similarly to Klemelä and Tsybakov [11]. Precisely, we will use a two-staged procedure in the spirit of Lepski’s method, constructing first a collection of admissible estimators and selecting then an estimator with minimal variance among them. In contrast to the Gaussian white noise setting considered in Klemelä and Tsybakov [11], the complexity of the multidimensional diffusion model however requires a more involved investigation and more sophisticated tools. This remark applies both to the proof of asymptotic lower and upper bounds on the pointwise risk. In particular, for proving the exact upper bound, sufficiently precise exponential bounds on the stochastic error are needed. In the Gaussian white noise framework, the derivation of such exponential bounds is straightforward due to the Gaussian nature of the model. An additional complication arises in the classical problem of estimating a density at some fixed point \(x_0\in \mathbb {R}\) from i.i.d. observations (cf. Butucea [3]) where one has to derive exponential bounds on the risk which hold uniformly over a set of estimators associated to different bandwidths. To do so, Butucea [3] uses the classical Bernstein inequality and a uniform exponential inequality due to van de Geer [24]. Similarly to the pointwise density estimation problem, the bandwidths used for defining the estimators in our selection procedure involve an estimator \(\widehat{\rho }_T(x_0)\) of the (unknown) value of the invariant density \(\rho _{b}\) at \(x_0\) such that uniform risk bounds on the stochastic error are required.
We proceed by introducing central assumptions on the diffusion process \(X\) required for proving adaptivity of the proposed estimation scheme. Let \(P_t\) be the transition semigroup of \(X\), and denote its transition density by \(p_t\), i.e.
The following Bernstein-type deviation inequality in particular allows to prove uniform deviation inequalities which are crucial tools for verifying sufficiently sharp upper bounds on the pointwise squared risk of the adaptive estimators. Given any \(b\in \Pi _0(\sigma )\), denote by \(\varsigma _b^2(\cdot )\) the asymptotic variance appearing in the CLT, i.e.
Assumption (BI)
Let \(b\in \varPi _0(\sigma )\). Then there exists some positive constant \(C_B\) such that, for any bounded measurable function \(f\in L^2(\mu _b)\) and for any \(r,T>0\) and \(j \in \{1,\ldots ,d\}\) fixed,
The investigation of the variance term in (4.1) differs from the case of independent data as there appear additional covariances in the dependent case. The following assumption provides sufficiently tight upper bounds on the (asymptotic) variance.
Assumption (SG+)
The carré du champs associated with the infinitesimal generator of the diffusion satisfies the spectral gap inequality, that is, for some constant \(c_P\) and any \(f \in L^2(\mu _b)\),
Furthermore, there exists some \(C_0>0\) such that, for any \(u\ge t>0\) and for any pair of points \(x,y\in \mathbb {R}^d\) with \(\Vert x-y\Vert ^2\le u\), the transition density \(p_t(\cdot ,\cdot )\) satisfies
For any symmetric diffusion \(X\), it can be shown analogously to the proof of Proposition 1 in Dalalyan and Reiß [7] (also see the proof of Lemma 2.3 in Cattiaux et al. [4]) that, for any \(f \in L^2(\mu _b)\) and \(T>0\),
The last term is upper-bounded by applying the Cauchy–Schwarz and the spectral gap inequality such that, for some positive constant \(C\) (depending only on \(c_P\)),
It however turns out that, given the goal of describing the precise asymptotics for nonparametric drift estimation, we do actually require an exponential inequality with a tight leading term in the exponent. Taking also into account the upper bound on the transition density in (4.2), Proposition 1 in Dalalyan and Reiß [7] provides an enforced upper bound on the variance of additive functionals of multidimensional diffusions which allows to prove such a refined exponential inequality. In particular, for any compactly supported kernel \(G:\mathbb {R}^d\rightarrow \mathbb {R}\), Assumption (SG+) ensures that there exists some positive constant \(C'\) (depending only on \(d\), \(C_0\) and \(c_P\)) such that, for any bandwidth \(h>0\), \(y\in \mathbb {R}^d\), \(T>0\),
It seems to be rather unconventional to investigate estimators in diffusion models under the explicit assumption that functional inequalities in the spirit of the spectral gap hypothesis are satisfied. We believe that this approach is useful as it allows to formulate precise results for a sufficiently large class of diffusion processes under clear assumptions; see in particular Theorem 3 below.
The adaptive scheme is based on Lepski’s principle. For implementing the procedure, consider a sufficiently fine grid \(\mathcal {G}=\mathcal {G}_T\) on the interval \(\left[ \beta _*,\beta _T\right] \), with \(\beta _T\rightarrow \infty \). It is defined as \(\mathcal {G}= \mathcal {G}_T:= \big \{\beta _1,\ldots ,\beta _m\big \}\), where \(\beta _*< \beta _1 < \cdots < \beta _m = \beta _T\). Assume that there exist \(k_2>k_1>0\) and \(\delta _1 \ge \delta >1\) such that
and set \(\beta _0 := \beta _*-d/2\). As in the case of density estimation from i.i.d. observations (cf. Butucea [3]), the optimal bandwidth for estimating \(b^j\rho _{b}\) is not available in practice as it involves the unknown value of the invariant density \(\rho _{b}\) at \(x_0 \in \mathbb {R}^d\). The adaptive procedure for estimating \(b^j\rho _{b}\) therefore starts with a preliminary estimator \(\widehat{\rho }_T(x_0)\) of the value \(\rho _{b}(x_0)\).
Definition of the preliminary density estimator Define
where \(Q\) is a bounded positive kernel satisfying \(\int _{\mathbb {R}^d}\Vert u\Vert |Q(u)|\mathrm {d}u < \infty \), and the bandwidth \(h_T>0\) is such that
and, for some \(\alpha _0 \in (0,1/2)\),
Recall the definition of \(\rho _T^*\), and let \(\widehat{\rho }_T(x_0) := \max \big \{\check{\rho }_T(x_0),\ \rho _T^*\big \}\).
Main part of the procedure: adaptive estimation of \(b\rho _{b}\) For fixed \(j \in \{1,\ldots ,d\}\), we now describe the procedure for defining an adaptive estimator of the \(j\)-th component of the vector \(b\rho _{b}\). Recall that \(\sigma \) is the dispersion matrix taking values in \(\mathbb {R}^{d\times d}\) and \(a=\sigma \sigma ^\top \) denotes the associated diffusion coefficient. The adaptive estimator will be selected among the family of estimators \(\widehat{g}^j_{T,\beta }(x_0)\), defined as
where \(\widehat{h}_{T,\beta } = \widehat{h}^j_{T,\beta } := \left( \frac{d\widehat{\rho }_T(x_0)a_{j j}\log T}{\beta T}\right) ^{1/(2\beta )}\). As in Klemelä and Tsybakov [10], the kernel \(K_\beta \) is obtained as a renormalized version of the basic kernel
namely
As the last ingredient of the adaptive procedure, introduce the thresholding sequence
The adaptive estimator \(\widetilde{g}_T^j\) is defined as
where
We continue with the main result on pointwise adaptive estimation of \(b\rho _{b}\). Recall the definition of the constants \(C_j(\beta ,L;\rho _{b},\sigma )\), \(j=1,\ldots ,d\), in (3.3). Denote by \(\widetilde{\varPi }(c_1,c_2)=\widetilde{\varPi }(c_1,c_2,\sigma )\) the intersection of \(\varPi (c_1,c_2,\sigma )\) with the set of all drift functions \(b\in \varPi _0(\sigma )\) satisfying (BI) and Assumption (SG+).
Theorem 2
For fixed \(\beta _*>d/2\), \(0<L_*<L^*<\infty \), \(\delta \in (0,1)\) and for \({\mathcal {B}}_T=\left[ \beta _*,\beta _T\right] \times \left[ L_*,L^*\right] \), where \(\beta _T = (\log \log T)^\delta \), the adaptive estimator \(\widetilde{g}_T^j\) defined according to (4.9) satisfies, for any \(x_0 \in \mathbb {R}^d\),
5 Sharp adaptive drift estimation for Kolmogorov diffusions
Restriction to the important case of Kolmogorov diffusions allows to derive and formulate results in a comparatively concise way.
Let \(b\in \varPi _0(\sigma _0~\mathbf {Id})\), \(0\ne \sigma _0\in \mathbb {R}\), and consider the diffusion
where \(W\) is a \(d\)-dimensional Brownian motion and the initial value \(X_0\) is independent of \(W\). Note that property \((\mathrm{P }_0')\) in the definition of the functional set \(\varPi _0\) is fulfilled if \(b=\sigma _0^2\nabla \left( \log \rho _b\right) /2\), that is, the drift vector \(b\) can be represented as a gradient. To enlighten notation, let
We further introduce the maximal risk of an estimator \(\check{g}_T\) of \(b\rho _{b}\), for \(\beta >d/2\), \(L>0\), \(T>0\), some bounded set \(A\subset \mathbb {R}^d\) and fixed \(x_0\in \mathring{A}\) defined as
Theorem 3
Define \({\mathcal {B}}_T\) as in Theorem 2, and consider the risk introduced in (5.3). Then the following holds true:
-
(a)
For any \(x_0\) and for \(C(\beta ,L;\rho _{b},\sigma _0)\) defined in (5.2), the estimator \(\widetilde{g}_T = \big (\widetilde{g}_T^j\big )_{j=1,\ldots ,d}\) defined according to (4.9) is sharp adaptive.
-
(b)
If there exists an estimator \(\check{g}_T\) such that, for some \(\beta _0 \ge \beta _*\), \(L>0\),
$$\begin{aligned} \limsup _{T\rightarrow \infty }\sup _{b \in \widetilde{\varPi }(c_1,c_2)}\sup _{\rho _b\in \varSigma _T(\beta _0,L;L', \sigma _0\mathbf {Id})} \frac{\mathbf {E}_b\Vert \check{g}_T(x_0)-(b\rho _{b})(x_0)\Vert ^2}{\psi _{T,\beta _0}^2 C^2(\beta _0,L;\rho _{b},\sigma _0)} < 1, \end{aligned}$$then there exists \(\beta _0' > \beta _0\) such that
$$\begin{aligned} \frac{{\fancyscript{R}}_{T,\beta _0',L}\big (\check{g}_T\big )}{{\fancyscript{R}}_{T,\beta _0',L}\big (\widetilde{g}_T\big )} \ge \varPsi _T\ \frac{{\fancyscript{R}}_{T,\beta _0,L}\big (\widetilde{g}_T\big )}{{\fancyscript{R}}_{T,\beta _0,L}\big (\check{g}_T\big )}, \end{aligned}$$(5.4)where \(\varPsi _T\rightarrow _{T\rightarrow \infty }\infty \). In particular, for any fixed \(\beta \ge \beta _*\), \(L>0\),
$$\begin{aligned} \limsup _{T\rightarrow \infty }\sup _{b \in \widetilde{\varPi }(c_1,c_2)}\sup _{\rho _b\in \varSigma _T(\beta ,L;L', \sigma _0\mathbf {Id})} \frac{\mathbf {E}_b\Vert \widetilde{g}_T(x_0)-(b\rho _{b})(x_0)\Vert ^2}{\psi _{T,\beta }^2 C^2(\beta ,L;\rho _{b},\sigma _0)} = 1. \end{aligned}$$
The statement in the second part of the above theorem is to be interpreted in the sense that, whenever there exists an estimator \(\check{g}_T\) which performs better than the estimator \(\widetilde{g}_T\) at least for one smoothness degree \(\beta _0\), there exists another smoothness factor \(\beta _0'\) for which there is much greater loss of \(\check{g}_T\). The assertion—and its respective proof—are to be compared with Theorem 2 in Klemelä and Tsybakov [11].
Proof (of Theorem 3)
We first show that \(\varPi (c_1,c_2,\sigma _0~\mathbf {Id})=\widetilde{\varPi }(c_1,c_2,\sigma _0~\mathbf {Id})\). Let \(b\in \varPi (c_1,c_2,\sigma _0~\mathbf {Id})\). In view of the results in Section 4.3 in Bakry et al. [2] (p. 747), \((\mathrm{P_1 })\) implies that (SG) holds. Since, in addition, \((\mathrm{P_2 })\) is satisfied, Theorem 3.2 in Qian and Zheng [17] entails that (4.2) and thus Assumption \((\mathrm{\mathbf {SG+} })\) is fulfilled. For any \(b\in \varPi _0(\sigma _0~\mathbf {Id})\), the associated measure \(\mu _b\) is reversible for \(X\) (see, e.g., Lemma 2.2.3 in Royer [19]). In particular, (SG) is equivalent to Poincaré’s inequality. Restricting to bounded drift functions, Poincaré’s inequality implies that Assumption (BI) is satisfied, too; this follows from Lemma 2 stated in Appendix A. In view of Theorem 1 and Theorem 2, it now only remains to verify (5.4). The proof actually is along the lines of the proof of Theorem 2 in Klemelä and Tsybakov [11] and therefore omitted. \(\square \)
We conclude this section with a brief summary of the adaptive estimation procedure. Assume that a continuous record of observations \(X^T=(X_t)_{0\le t\le T}\) of a diffusion process solution of the SDE (2.1) is available and that the (constant) diffusion matrix \(a=\sigma \sigma ^\top \) is known. The goal is to estimate the value of the \(j\)-th component of the product \(b\rho _b\) at some given fixed point \(x_0\). For implementing the adaptive estimation scheme, we need to specify a lower bound \(\beta _*>d/2\) on the unknown smoothness of the function \(b\rho _b\) and fix some value \(\delta \in (0,1)\). To define an estimator on the basis of the input parameters \(X^T\), \(a=(a_{ij})_{1\le i,j\le d}\), \(x_0\), \(\beta _*\) and \(\delta \), one then might proceed as follows:
- \(*\) :
-
(Computation of a pilot estimator of the invariant density) Choose some bounded positive kernel \(Q:\mathbb {R}^d\rightarrow \mathbb {R}\) satisfying \(\int _{\mathbb {R}^d}\Vert u\Vert |Q(u)|\mathrm {d}u<\infty \) and some bandwidth \(h_T>0\) fulfilling (4.6). Define a preliminary density estimator \(\widehat{\rho }_T(x_0)\) by computing \(\check{\rho }_T(x_0)\) according to (4.5) and by letting
$$\begin{aligned} \widehat{\rho }_T(x_0):=\max \left\{ \check{\rho }_T(x_0), \ \rho _T^*\right\} , \end{aligned}$$where \(\rho _T^*\) denotes a vanishing sequence of positive real numbers satisfying \(\liminf _{T\rightarrow \infty }(\rho _T^*\log T)>0\).
- \(*\) :
-
(Computation of kernel estimators for a discrete set of parameters) Specify a grid \(\mathcal {G}_T:=\{\beta _1,\ldots ,\beta _m\}\), where the values \(\beta _*<\beta _1<\cdots <\beta _m=(\log \log T)^\delta \) are chosen such that (4.4) is satisfied. Define the bandwidths
$$\begin{aligned} \widehat{h}_{T,\beta _i}=\left( \frac{d\widehat{\rho }_T(x_0)a_{jj}\log T}{\beta _i T}\right) ^{\frac{1}{2\beta _i}},\quad i=1,\ldots ,m. \end{aligned}$$Recall the definition of the kernel \(K_\beta \) in (4.8), and compute the family of estimators
$$\begin{aligned} \widehat{g}_{T,\beta _i}^j(x_0)=\frac{1}{T\widehat{h}_{T,\beta _i}^d}\int _0^T K_{\beta _i}\left( \frac{X_u-x_0}{\widehat{h}_{T,\beta _i}}\right) \mathrm {d}X_u^j,\quad i=1,\ldots ,m. \end{aligned}$$(5.5) - \(*\) :
-
(Definition of the Lepski-type estimator of \(\beta \) and the adaptive estimator of \(b^j\rho _b\)) Recall the definition of \(\mathbb {I}_\beta ^2\) in (1.4), and define the thresholding values
$$\begin{aligned} \widehat{\eta }_{T,\beta _i}=\left( \frac{d\widehat{\rho }_T(x_0)a_{jj}\log T}{\beta _i T}\right) ^{\frac{\beta _i-d/2}{2\beta _i}} {\mathbb {I}}_{\beta _i}\left( \frac{2\beta _i-d}{d} \right) ^{\frac{\beta _i+d/2}{2\beta _i}},\quad i=1,\ldots ,m.\nonumber \\ \end{aligned}$$(5.6)Use the values (5.5) and (5.6) to determine \(\widehat{\beta }_T^j\) as specified in (4.10), and define the adaptive estimator \(\widetilde{g}_T^j(x_0)=\widehat{g}^j_{T,\widehat{\beta }_T^j}(x_0)\).
Remark 2
-
Once one has determined the adaptive estimator \(\widetilde{g}_T=(\widetilde{g}_T^j)_{j=1,\ldots ,d}\) according to the above scheme, one obtains an adaptive drift estimator by defining a suitable invariant density estimator \(\widetilde{\rho }_T\) and setting
$$\begin{aligned} \widetilde{b}_T(x_0) := \frac{\widetilde{g}_T(x_0)}{\widetilde{\rho }_T(x_0) \vee \rho _*(x_0)}, \qquad x_0\in \mathbb {R}^d, \end{aligned}$$\(\rho _*(x_0)> 0\) denoting some a priori lower bound on \(\rho _{b}(x_0)\). Restricting again to the case of Kolmogorov diffusions as in (5.1), the normalizing factor appearing in the upper bound for the pointwise squared risk of \(\widetilde{b}_T^j(x_0)\), assuming that \(b \in \varPi (c_1,c_2)\) and \(\rho _b\in \varSigma _T(\beta ,L;L',\sigma _0~\mathbf {Id})\), is identified as \(C_j(\beta ,L;\rho _{b},\sigma _0)\rho _{b}^{-1}(x_0) = D_j(\beta ,L;\rho _{b},\sigma _0)\).
-
In the situation of Theorem 3, an explicit a priori lower bound on \(\rho _b(x_0)\) depending only on \(c_1,c_2\) can be derived as in Remark 6 in Dalalyan and Reiß [7]. For the more general case of diffusion processes with uniformly nondegenerate diffusion matrix \(a\), it was proven in Metafune et al. [15] that, if \(b^i \in C^2(\mathbb {R}^d)\), \(\mathrm{(P_1) }\) is satisfied, and, in addition, \(\Vert b(x)\Vert +\Vert Db(x)\Vert +\Vert D^2b(x)\Vert \le c_1'(1+\Vert x\Vert )\) for some constant \(c_1'>0\), it holds \(\rho _b(x)\ge \mathrm {e}^{-K(1+\Vert x\Vert ^2)}\), \(x\in \mathbb {R}^d\), with some positive constant \(K\) depending only on \(c_1'\), \(c_2\), \(d\) and \(\sigma \).
6 Discussion and extensions
Placement and interpretation of the identified constants Let us first arrange the normalizing factors identified in the previous sections and relate it to known results on asymptotically exact adaptive estimation with respect to pointwise risk over the scale of Sobolev classes in the classical statistical models. Tsybakov [23] considers the problem of nonparametric function estimation in the Gaussian white noise model (in the one-dimensional case), assuming that the unknown function belongs to some Sobolev class with unknown regularity parameter. The question of density estimation at a fixed point \(x_0 \in \mathbb {R}\) is investigated by Butucea [3]. Since the variance of the proposed kernel estimator is proportional to the value of the unknown density \(f\) at \(x_0\), the value \(f(x_0)\) appears in the exact normalization. Klemelä and Tsybakov [11] deal with nonparametric estimation of a multivariate function and its partial derivatives at a fixed point when the Riesz transform is observed in Gaussian white noise. In particular, Klemelä and Tsybakov [11] find the exact constant for nonparametric estimation of a function \(f: \mathbb {R}^d \rightarrow \mathbb {R}\), observed in Gaussian white noise and satisfying the Sobolev smoothness constraint \(\eta _\beta (f) \le L\). In combination with the results of Butucea [3] on classical density estimation (in dimension \(d=1\)), the exact constant for nonparametric estimation of a density \(f:\mathbb {R}^d\rightarrow \mathbb {R}\) at some fixed point \(x_0\in \mathbb {R}^d\) is then identified as
For the case of Kolmogorov diffusions with \(\sigma \sigma ^\top = \mathbf {Id}\), \(C_j(\beta ,L;\rho _{b},\mathbf {Id})\) as introduced in (3.3) coincides with the constant in (6.1). The accordance of constants in the exact asymptotics reflects the old-established experience that different statistical models show similar behavior, at least from an asymptotic point of view. The remarkable results of Dalalyan and Reiß [7] on asymptotic statistical equivalence for inference on the drift in multidimensional Kolmogorov diffusion models justify this notice in a mathematically formal manner. They are however established under rather restrictive (Hölder) smoothness assumptions. Precisely, the critical regularity for proving asymptotic equivalence with the Gaussian shift model grows like \((1/2+1/\sqrt{2})d\) as \(d \rightarrow \infty \). The authors refer to the question whether for Hölder classes of smaller regularity asymptotic equivalence fails as “a challenging open problem.” Our risk bounds are valid under weaker smoothness constraints which suggests that asymptotic equivalence (at least in a reduced sense) still holds beyond the critical bounds of Dalalyan and Reiß [7]. Going beyond the special case of Kolmogorov diffusions with unit diffusion part, the dependence of the drift estimation problem on the form of the diffusion coefficient \(a=\sigma \sigma ^\top \) is reflected by the appearance of the \(j\)-th diagonal entry of the matrix \(a\) in the optimal normalizing factor \(C_j(\beta ,L;\rho _{b},\sigma )\) (for estimating \(b^j\rho _{b}\)).
Possible generalizations of the assumptions It can be argued which type of description of the dependence structure underlying the diffusion is most convenient. Given the goal of describing exact asymptotics for pointwise drift estimation for an as large as possible class of diffusion processes under some preferably small set of assumptions, we decided to formulate our results in terms of the spectral gap hypothesis. Indeed, restricting to the case of reversible diffusion processes, Theorem 3.1 in Guillin et al. [8] implies that, whenever \(\varsigma _b^2(g)\le C \Vert g\Vert _\infty ^2\) for any centered bounded \(g\) and some constant \(C>0\), (BI) entails the Poincaré inequality, i.e.
for any smooth enough function \(f:\mathbb {R}^d\rightarrow \mathbb {R}\) and some positive constant \(c_P\). It is further well-known that Poincaré’s inequality in the symmetric case is equivalent to the spectral gap assumption (SG). However, as was already noted in the introduction, the upper bound result in Theorem 2 essentially holds whenever a Bernstein-type deviation inequality in the spirit of (BI) is combined with a sufficiently tight upper variance bound [as provided by Assumption (SG+)]. Such variance bounds for diffusion processes actually can be deduced by means of mixing conditions or the assumption of weak dependence of data.
References
Aït-Sahalia, Y.: Closed-form likelihood expansions for multivariate diffusions. Ann. Stat. 36(2), 906–937 (2008)
Bakry, D., Cattiaux, P., Guillin, A.: Rate of convergence for ergodic continuous Markov processes: Lyapunov versus Poincaré. J. Funct. Anal. 245(3), 727–759 (2008)
Butucea, C.: Exact adaptive pointwise estimation on Sobolev classes of densities. ESAIM: Prob. Stat. 5, 1–31 (2001)
Cattiaux, P., Chafaï, D., Guillin, A.: Central limit theorems for additive functionals of ergodic Markov diffusions processes. ALEA, Lat. Am. J Probab. Math. Stat. 9(2), 337–382 (2012)
Dalalyan, A.S.: Sharp adaptive estimation of the drift function for ergodic diffusions. Ann. Stat. 33(6), 2507–2528 (2005)
Dalalyan, A.S., Kutoyants, Y.A.: Asymptotically efficient trend coefficient estimation for ergodic diffusion. Math. Methods Stat. 11, 402–427 (2002)
Dalalyan, A.S., Reiß, M.: Asymptotic statistical equivalence for ergodic diffusions: the multidimensional case. Probab. Theory Relat. Fields 137(1), 25–47 (2007)
Guillin, A., Léonard, C., Wu, L., Yao, N.: Transportation-information inequalities for Markov processes. Probab. Theory Relat. Fields 144(3–4), 669–695 (2009)
Itō, K., McKean, H.P.: Diffusion Processes and their Sample Paths. Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen, vol. 125. Springer, Berlin (1965)
Klemelä, J., Tsybakov, A.B.: Sharp adaptive estimation of linear functionals. Ann. Stat. 29(6), 1567–1600 (2001)
Klemelä, J., Tsybakov, A.B.: Exact constants for pointwise adaptive estimation under the Riesz transform. Probab. Theory Relat. Fields 129, 441–467 (2004)
Lepski, O.V.: One problem of adaptive estimation in Gaussian white noise. Theory Probab. Appl. 35, 459–470 (1990)
Lezaud, P.: Chernoff and Berry–Esséen inequalities for Markov processes. ESAIM: Probab. Stat. 5, 183–201 (2001)
Liptser, R.S., Shiryaev, A.N.: Statistics of Random Processes. General Theory of Applications of Mathematics: Stochastic Modelling and Applied Probability, vol. 1, 2nd edn. Springer, Berlin (2001)
Metafune, G., Pallara, D., Rhandi, A.: Global properties of invariant measures. J. Funct. Anal. 223(2), 396–424 (2005)
Parzen, E.: On estimation of a probability density function and mode. Ann. Math. Stat. 33(3), 1065–1076 (1962)
Qian, Z., Zheng, W.: A representation formula for transition probability densities of diffusions and applications. Stoch. Process. Appl. 111(1), 57–76 (2004)
Revuz, D., Yor, M.: Continuous Martingales and Brownian Motion. Grundlehren der mathematischen Wissenschaften, vol. 293, 3rd edn. Springer, Berlin (1999)
Royer, G.: An initiation to logarithmic Sobolev inequalities. Collection SMF: Cours spécialisés. American Mathematical Society (2007)
Spokoiny, V.G.: Adaptive drift estimation for nonparametric diffusion model. Ann. Stat. 28(3), 815–836 (2000)
Strauch, C.: Sharp adaptive drift estimation and Donsker-type theorems for multidimensional ergodic diffusions. Ph.D. thesis, Universität Hamburg (2013)
Stroock, D.W., Varadhan, S.R.S.: Multidimensional Diffusion Processes. Grundlehren der mathematischen Wissenschaften, vol. 233. Springer, Berlin, New York (1979)
Tsybakov, A.B.: Pointwise and \(\sup \)-norm sharp adaptive estimation of functions on the Sobolev classes. Ann. Stat. 26(6), 2420–2469 (1998)
van de Geer, S.: Empirical Processes in M-Estimation. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press, Cambridge (2000)
van der Vaart, A.W., Wellner, J.W.: Weak Convergence and Empirical Processes. Springer Series in Statistics. Springer, New York (1996)
Acknowledgments
The author is grateful to her Ph.D. advisor, Angelika Rohde, and Enno Mammen for constant encouragement and constructive advise. She also would like to thank two anonymous referees for helpful comments which led to a substantial improvement of the paper. This work was partially supported by the DFG Priority Program SPP 1324 (Project: RO 3766/2-1).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Preliminaries
We first give a result which allows to deduce the exact asymptotics for pointwise estimation of the drift component \(b^j\) from exact results on estimating \(b^j\rho _{b}\), \(j\in \{1,\ldots ,d\}\). In particular, it allows to identify \(D(\beta ,L;\rho _b,\sigma _0)\) as defined in (1.3) as the optimal normalizing factor for estimating the \(j\)-th component of \(b\in \varPi (c_1,c_2,\sigma _0\mathbf {Id})\). For the detailed derivation of the exact lower bound, we refer to Theorem 2.5.7 in Strauch [21].
Lemma 1
-
(a)
There exist two positive constants \(C_1,C_2\) (depending only on \(c_1\), \(c_2\) and \(\sigma )\) such that the invariant density \(\rho _{b}\) satisfies \(\rho _{b}(x) \le C_1\mathrm {e}^{-C_2\Vert x\Vert ^2}\), \(x \in \mathbb {R}^d\), for any \(b\in \varPi (c_1,c_2)\).
-
(b)
If \(b\in \widetilde{\varPi }(c_1,c_2)\) and if \(\rho _{b} \in {\mathcal {S}}(\beta +1,L')\), for some \(\beta >d/2\) and \(L' > 0\), then there exists an invariant density estimator \(\widehat{\rho }_T\) such that
$$\begin{aligned} \mathbf {E}_b|\widehat{\rho }_T(x)-\rho _{b}(x)|^{2} \le K_1 T^{-\frac{\beta +1-(d/2)}{\beta +1}} \exp \left( -K_2\Vert x\Vert \right) \!, \qquad x \in \mathbb {R}^d, \end{aligned}$$(7.1)where the constants \(K_1,K_2\) depend only on \(L',c_1,c_2\) and \(\sigma \).
Proof
-
(a)
The pointwise upper bound on \(\rho _b\) is an immediate consequence of the results of Metafune et al. [15] who study global regularity properties of invariant measures of divergence-form operators. Their results also hold in our specific framework since we restrict attention to the case of constant, uniformly elliptic diffusion part. Denote by \(\lambda _{\max }\) the largest eigenvalue of \(a\). Due to Corollary 2.5 in Metafune et al. [15], \(\mathrm{(P_1) }\) implies that \(\exp (\eta \Vert x\Vert ^2) \in L^1(\mu _b)\) for \(\eta < c_1\left( 2\lambda _{\max }\right) ^{-1}\). Since \(\left\| b(x)\right\| \le c_2(1+\Vert x\Vert )\lesssim \exp (\Vert x\Vert )\), Theorem 6.1 in Metafune et al. [15] applies and yields the assertion.
-
(b)
Let \(G=G_{\beta +1}:\mathbb {R}^d\rightarrow \mathbb {R}\) be the kernel with Fourier transform
$$\begin{aligned} \phi _G(\lambda ) = \int _{\mathbb {R}^d} \mathrm {e}^{\mathrm{i }\lambda ^\top y} G(y)\mathrm {d}y = \frac{1}{1+\Vert \lambda \Vert ^{2(\beta +1)}}, \quad \lambda \in \mathbb {R}^d, \end{aligned}$$and define the invariant density estimator
$$\begin{aligned} \widehat{\rho }_T(x)=\widehat{\rho }_{T,h}(x) := \frac{1}{T h^d} \int _0^T G\left( \frac{X_u-x}{h}\right) \mathrm {d}u, \quad x \in \mathbb {R}^d. \end{aligned}$$The bandwidth \(h = h_T \searrow 0\) is to be specified later. For bounding the stochastic error, note that, using (4.3),
$$\begin{aligned} \mathbf {E}_b \big |\widehat{\rho }_T(x)-\mathbf {E}_b \widehat{\rho }_T(x)\big |^2&= \frac{1}{T^2h^{2d}}\ \mathrm{Var }_b\Bigg (\int _0^T G\left( \frac{X_u-x}{h}\right) \mathrm {d}u\Bigg ) \\&\le \frac{C}{T h^{2d}} \int _{\mathbb {R}^d} G^2\left( \frac{y-x}{h}\right) \rho _{b}(y)\mathrm {d}y. \end{aligned}$$Taking into account the regularity properties of \(G\), a multidimensional version of Theorem 1A in Parzen [16] yields
$$\begin{aligned} \mathbf {E}_b \big |\widehat{\rho }_T(x)-\mathbf {E}_b \widehat{\rho }_T(x)\big |^2 \le \frac{C}{Th^d} \rho _{b}(x)\Vert G\Vert _{L^2(\mathbb {R}^d)}^2 (1+o_T(1)). \end{aligned}$$It remains to treat the bias term. Note that, using in particular Cauchy–Schwarz,
$$\begin{aligned} \big |\mathbf {E}_b \widehat{\rho }_T(x)-\rho _{b}(x)\big |&= (2\pi )^{-d} \left| \int _{\mathbb {R}^d}\phi _{\rho _{b}}(\lambda )\left\{ \left( 1+\Vert h\lambda \Vert ^{2\beta }\right) ^{-1}-1\right\} \mathrm {e}^{-\mathrm{i }\lambda ^\top x}\mathrm {d}\lambda \right| \\&\le h^{\beta + 1}\left( (2\pi )^{-d}\int _{\mathbb {R}^d}\left| \phi _{\rho _{b}} (\lambda )\right| ^2\Vert \lambda \Vert ^{2(\beta +1)}\mathrm {d}\lambda \right) ^{1/2}\\&\quad \times \left( (2\pi )^{-d}\int _{\mathbb {R}^d}\frac{\left\| h\lambda \right\| ^{2(\beta +1)}}{\left( 1+\Vert h\lambda \Vert ^{2(\beta +1)}\right) ^2} \mathrm {d}\lambda \right) ^{1/2}\\&\le L' ~ (2\pi )^{-d/2}\left( \int _{\Vert y\Vert \le 1}\frac{\mathrm {d}y}{(1+\Vert y\Vert ^{2\beta })^2} + \int _{\Vert y\Vert >1} \frac{\mathrm {d}y}{\Vert y\Vert ^{2\beta }}\right) ^{1/2}\\&\quad \times h^{\beta +1-d/2} =: M h^{\beta +1-d/2}. \end{aligned}$$Specifying \(h = h_T \sim \left( \frac{C\rho _{b}(x)}{M^2T}\right) ^{\frac{1}{2(\beta +1)}}\) and using the upper bound on \(\rho _b(x)\) from part (a), we obtain (7.1). \(\square \)
Denote by \(N_{[\,]}\left( \varepsilon ,\mathcal {F},L^2(\mu _b)\right) \) the \(\varepsilon \)-entropy with bracketing, that is, the smallest number of \(\varepsilon \)-brackets (in \(L^2(\mu _b)\)) which are required to cover \(\mathcal {F}\) (cf. van der Vaart and Wellner [25], Definition 2.1.6).
Lemma 2
-
(a)
Let \(b\in \varPi (c_1,c_2,\sigma )\), and suppose that \(X\) satisfies (PI). Fix \(j \in \{1,\ldots ,d\}\), and assume that there exists some positive constant \(B\) such that, for any bounded measurable \(f\in L^2(\mu _b)\),
$$\begin{aligned} \max \bigg \{\sup _{x \in \mathrm{supp}(f)} |b^j(x)|,\sup _{x \in \mathrm{supp}(f^2)} |b^j(x)|^2\bigg \} \le B. \end{aligned}$$(7.2)Then Assumption (BI) is satisfied.
-
(b)
Let \(\mathcal {F}\subset L^2(\mu _b)\) be some class of measurable functions \(f: \mathbb {R}^d \rightarrow \mathbb {R}\), and assume that, for some positive constants \(K\) and \(M\), it holds
$$\begin{aligned} \sup _{f \in \mathcal {F}} \Vert f\Vert _\infty \le K, \quad \sup _{f \in \mathcal {F}}\Vert f\Vert _{L^2(\mu _b)} \le M. \end{aligned}$$Grant Assumptions (BI) and (SG). Then, for arbitrary \(T >0\) and any positive \(r\) satisfying, for some positive constants \(K_1\) and \(K_2\),
$$\begin{aligned} \frac{K_1}{\sqrt{T}}\int _0^1 \max \left\{ \sqrt{\log N_{[\ ]}(\varepsilon ,\mathcal {F},L^2(\mu _b))},1\right\} \mathrm {d}\varepsilon ~ \le ~ r ~ \le ~ \frac{K_2M^2}{K}, \end{aligned}$$there exist some positive constants \(C_1\) and \(C_2\) such that
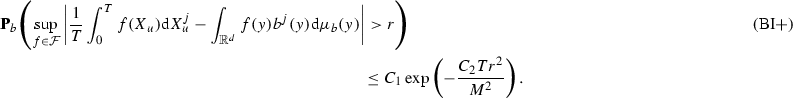
Proof
(a) Letting, for \(r,T>0\),
Theorem 1.1 in Lezaud [13] implies that
Using the spectral gap assumption, we get, for any \(T>0\), \(g \in L^2(\mu _b)\),
Consequently, in view of (7.2),
and \(\Vert fb^j\Vert _\infty \le B \Vert f\Vert _\infty \). Plugging these estimates into (7.4), we obtain the asserted inequality.
(b) Under the given assumptions, Bernstein’s inequality for continuous martingales can be used to show that there exists some constant \(\widetilde{C}_B\) such that, for any \(r,T>0\),
To see this, write \(\mathsf {q}_T(r) \le \mathsf {p}_T(r/2) + \mathsf {p}'_T(r/2)\), for \(\mathsf {p}_T(\cdot )\) introduced in (7.3) and
Letting \(M_t(f) := \int _0^t f(X_u)\sum _{k=1}^d \sigma _{jk}~ \mathrm {d}W_u^k\), \(t \ge 0\), and denoting by \(\langle M\rangle _\cdot \) the quadratic variation of the martingale \(M\), Bernstein’s inequality for continuous martingales (see p. 154 in Revuz and Yor [18]) gives
Theorem 1.1 in Lezaud [13] then can be used to show that
The inequality (7.5) now follows for \(\widetilde{C}_B := 4\max \big \{2c_P,2c_Pa_{jj}^2,c_Pa_{jj},1\big \}\). In view of (7.5), a uniform exponential inequality in the spirit of Theorem 5.11 in van de Geer [24] is available. Indeed, Theorem 5.11 in van de Geer [24] appears as a special case of the uniform inequality for martingales in van de Geer [24]’s Theorem 8.13, and the proof of Theorem 8.13 continues to hold in the diffusion setting if the Bernstein inequality for martingales in van de Geer [24]’s Corollary 8.10 is replaced with the Bernstein-type deviation inequality (BI). \(\square \)
For the proof of the following Lemma, we refer to the proofs of Proposition 1 in Klemelä and Tsybakov [10] and of Lemma 10 in Tsybakov [23].
Lemma 3
Let \(\beta >d/2\), and, for \(\mathbb {I}_\beta \), \(\widetilde{K}_\beta (\cdot )\) and \(\mathrm {b}= \mathrm {b}(\beta )\) defined according to (1.4), (4.7) and (4.8), respectively, let \(K_\beta ^*(x):= \mathbb {I}_\beta ^{-1} \mathrm {b}^{-\beta +d/2} \ \widetilde{K}_\beta (\mathrm {b}x)\).
-
(a)
(cf. Proposition 1 in Klemelä and Tsybakov [10]) It holds
$$\begin{aligned} \widetilde{K}_\beta (0) = (2\pi )^{-d} \int _{\mathbb {R}^d} \left( 1+\Vert \lambda \Vert ^{2\beta }\right) ^{-1}\mathrm {d}\lambda = \frac{2\beta }{d}\ \mathbb {I}_\beta ^2, \end{aligned}$$and, for \(K_\beta (x) = \mathrm {b}^d \widetilde{K}_\beta (\mathrm {b}x)\), \(\big \Vert K_\beta \big \Vert _{L^2(\mathbb {R}^d)} = \mathbb {I}_\beta \left( \frac{2\beta - d}{d}\right) ^{\frac{\beta +d/2}{2\beta }} = \mathbb {I}_\beta \ \mathrm {b}^{\beta +d/2}\).
-
(b)
(cf. Lemma 10 in Tsybakov [23]) For fixed \(\delta \in (0,1)\), there exists some compactly supported modification \(\overline{K}_\beta \) of \(K_\beta ^*\) which enjoys the following properties,
$$\begin{aligned} \big \Vert \overline{K}_\beta \big \Vert _{L^2(\mathbb {R}^d)}&\le 1-\delta /2, \end{aligned}$$(K1)$$\begin{aligned} \eta _\beta (\overline{K}_\beta )&\le 1-\delta /2, \end{aligned}$$(K2)$$\begin{aligned} (1-\delta /2) K_\beta ^*(0)&\le \overline{K}_\beta (0) \le K_\beta ^*(0). \end{aligned}$$(K3)
Appendix B: Proofs
1.1 B.1: Lower bound
Proof (of Theorem 1)
Let \(\psi _{\beta ,L} = \psi ^j_{\beta ,L} := \psi _{T,\beta } C_j(\beta ,L;\rho _{b},\sigma )\), for \(\psi _{T,\beta }\) and \(C_j(\beta ,L;\rho _{b},\sigma )\) defined in (3.1) and (3.3), respectively. To enlighten notation, the dependence on the coordinate \(j \in \{1,\ldots ,d\}\) will be mostly suppressed in the sequel.
(I) Construction of the hypotheses. Let \(L \in [L_*,L^*]\), fix some nondegenerate \(\mathbb {R}^{d\times d}\)-matrix \(\sigma \), let \(a:=\sigma \sigma ^\top \), and consider some positive density function
Fix \(\delta _{0} \in (0,1/2)\), \(c_1,c_2>0\), and assume that \(\rho \) is such that the function
satisfies \(\rho _{T,0}(x_0) \ge \rho _T^*\), for any \(x\) with \(\Vert x\Vert \) large enough,
and for any \(x\in \mathbb {R}^d\),
Consequently, \(a\nabla (\log \rho _{T,0})/2=:b_{T,0}\in \varPi (c_1,c_2,\sigma )\). In particular, the SDE \(\mathrm {d}X_t = b_{T,0}(X_t)\mathrm {d}t +\sigma ~ \mathrm {d}W_t\), \(t\ge 0\), admits a strong solution with Lebesgue continuous invariant measure and invariant density \(\rho _{T,0}\). Define further
For \(\beta >d/2\), consider \(\widetilde{K}_\beta \) and \(\mathrm {b}= \mathrm {b}(\beta )\) as introduced in (4.7) and (4.8), respectively, and denote again \(K_\beta ^*(x)=\mathbb {I}_\beta ^{-1} \mathrm {b}^{-\beta + d/2} ~ \widetilde{K}_\beta (\mathrm {b}x)\). Lemma 3 implies that
and
Denote by \(\overline{K}_\beta \) the compactly supported modification of \(K_\beta ^*\) from Lemma 3 satisfying (K1), (K2), and (K3) for \(\delta = \delta _0\). Define the function \(g_{T,\beta _*}: \mathbb {R}^d \rightarrow \mathbb {R}\) such that, for any \(k \in \{1,\ldots ,d\}\),
where
Let
and consider the hypothesis \(g_{T,1}\), defined as \(g_{T,1}:= \sum _{k=1}^d a_{jk}\partial _k\rho _{T,1}/2\). The function \(b_{T,1}:\mathbb {R}^d\rightarrow \mathbb {R}^d\) is taken as \(b_{T,1} := a\nabla (\log \rho _{T,1})/2\). Note that, for \(T\) large enough,
Plugging in the respective definitions of the hypotheses, it can be shown that \(g_{T,0}\in {\mathcal {S}}(\beta _T,L)\), \(g_{T,1} \in {\mathcal {S}}(\beta _*,L)\) and \(b_{T,1}\in \varPi (c_1,c_2,\sigma )\). The above definitions of the hypotheses further imply that \(\rho _{T,0}\in {\mathcal {S}}(\beta _T+1,L'), \rho _{T,1}\in {\mathcal {S}}(\beta _*+1,L')\) and
Summing up, \(\rho _{T,0}\in \varSigma _T(\beta _T,L)\) and \(\rho _{T,1}\in \varSigma _T(\beta _*,L)\).
(II) A version of Theorem 6(i) in Tsybakov [23]. The central ingredient of the proof is a special case of Theorem 6(i) in Tsybakov [23]. It will be applied in the following situation: Denote by \(\mathbf {E}_i = \mathbf {E}_{b_{T,i}}\) expectation under the measure \(\mathbf {P}_i = \mathbf {P}_{b_{T,i}}\) associated with the hypothesis \(b=b_{T,i}\), \(i \in \{0,1\}\), and note that
where \(Q_T := \psi _{\beta _*,L}\psi _{\beta _T,L}^{-1}\), \(\widehat{T}_T:= \psi _{\beta _*,L}^{-1}\big (\widehat{g}_T(x_0)-g_{T,0}(x_0)\big )\), and
The proof of the following lemma is completely along the lines of the proof of Theorem 6(i) in Tsybakov [23].
Lemma 4
(Theorem 6(i) in Tsybakov [23]) Consider \(Q_T\), \(\widehat{T}_T\) and \(\theta _1\) as introduced above, and assume that \(\theta _1 \in \mathbb {R}\) satisfies
If \(\mathbf {P}_0,\mathbf {P}_1\) are such that \(\mathbf {P}_0 \ll \mathbf {P}_1\) and, for \(\tau > 0\) and \(\alpha \in (0,1)\) fixed,
then
where the infimum is taken over all \(\widehat{T}_T= \psi _{\beta _*,L}^{-1}\big (\widehat{g}_T(x_0)-g_{T,0}(x_0)\big )\).
We proceed with verifying (A1) and (A2). Note first that
Since, for \(T\) large enough, \(\psi _{\beta _*,L}^{-1}\int _{\mathbb {R}^d}g_{T,\beta _*}(y) \mathrm {d}y \le \delta _0/2\), this implies
Denote by \(Y\) the solution of the SDE \(\mathrm {d}Y_t = b_{T,1}(Y_t)\mathrm {d}t+\sigma ~\mathrm {d}W_t\). In order to verify (A2), note that the specifications on pp. 296–297 in Liptser and Shiryaev [14] imply that the likelihood ratio under \(\mathbf {P}_1\) is given by
To proceed, set
denote \(g := (b_{T,0} -b_{T,1})^\top a^{-1}(b_{T,0} -b_{T,1})\), and consider the following stationary sequence of random variables,
Since \(g \in L^1(\mathbf {P}_1)\), it follows from the ergodic theorem that, for any \(t>0\),

where
In particular, this implies by means of the martingale CLT that, for some standard Brownian motion \(W\),

Denoting by \([s]\) the integer part of \(s\) and considering an arbitrary sequence \(\gamma (s)\rightarrow _{s\rightarrow \infty }0\), it holds

Choosing \(t\equiv 1\) in (8.8) and passing to the continuous-time case, we obtain

It is verified by straightforward algebra that the definition of the hypotheses \(b_{T,0} \) and \(b_{T,1}\) entails that
The definition of \(g_{T,\beta _*}\) further implies that, using in particular (8.1),
The last inequality follows from (K1). Thus, plugging in the definition of \(h_{T,\beta _*}\) [see (8.2)] and using (8.3),
It can be shown by analogous arguments that the terms
and
are asymptotically negligible. Thus, for \(c\) defined in (8.7) and whenever \(\delta _{0}\) is small and \(T\) is large enough,
Consequently, for \(\tau := \exp \left( -\frac{\left( 1-\delta _{0}^2/4\right) d\log T}{2\beta _*}\right) \), it holds a.s.
The verification of (A2) is accomplished by means of a tightness argument. Consider some sequence of probability measures \((\mathbf {P}_n)_{n\ge 1}\) on some measurable space, converging weakly to some probability measure \(\mathbf {P}\). Tightness of \(\mathbf {P}_n\) implies that, for any sequence \(\gamma _n\rightarrow -\infty \),
Thus, \(\lim _{m\rightarrow \infty }\sup _{n\in \mathbb {N}}\mathbf {P}_n\left( (-\infty ,\gamma _m)\right) = 0\) and \(\lim _{m\rightarrow \infty }\inf _{n\in \mathbb {N}}\mathbf {P}_n\left( (-\infty ,\gamma _m)\right) =1\). In particular,
In the current framework, this last assertion implies that, for
one has [plugging in (8.6)]
For large enough \(T\) and fixed \(\tau >0\) (where \(\delta _{0}\in (0,1)\) can be chosen arbitrarily small), we thus obtain
(III) Completion of the proof. In view of (8.5) and (8.9), Lemma 4 gives
Since, for \(C := C_j(\beta _*,L;\rho _{T,0},\sigma )/ C_j(\beta _T,L;\rho _{T,0},\sigma )\),
we have
As \(T \rightarrow \infty \), \(\tau Q_T^2 \rightarrow \infty \). Choosing \(\delta _{0} > 1/A\) for \(A\) large enough to ensure \(\delta _{0} < 1/2\), it holds
Taking now \(A\rightarrow \infty \), the assertion follows. \(\square \)
1.2 B.2: Upper bound
Proof (of Theorem 2)
Let \(\beta \in \left[ \beta _*,\beta _T\right] \), \(L\in \left[ L_*,L^*\right] \), \(\beta ' \in (d/2,\beta ]\), \(c_1\in (0,\infty ]\), \(c_2>0\), \(\sigma \) some nondegenerate \(\mathbb {R}^{d\times d}\)-matrix, \(L'>0\), and fix \(j \in \{1,\ldots ,d\}\).
Denote by \(\gamma _{Ti}\), \(i \in \mathbb {N}\), functions of \(T\) such that \(\lim _{T\rightarrow \infty }\gamma _{Ti} = 0\). For \(\psi _{T,\beta }\) and \(C_j(\beta ,L;\rho _{b},\sigma )\) introduced in (3.1) and (3.3), respectively, recall that \(\psi _{\beta ,L} = \psi _{\beta ,L}^j = \psi _{T,\beta } C_j(\beta ,L;\rho _{b},\sigma )\). To enlighten notation, the dependence on the coordinate \(j\) again will be mostly suppressed. Denote by \(\widetilde{T}(\beta )\) the effective noise level under adaptation, defined as
Consider the following deterministic counterparts of the bandwidth \(\widehat{h}_{T,\beta '}\) and the thresholding sequence \(\widehat{\eta }_{T,\beta '}\),
and
Set
Define \(\overline{\delta }_T := (\log T)^{-1}\), and introduce the random event
and the associated deterministic set \({\mathcal {H}}_{T,\beta '} \!=\! {\mathcal {H}}^j_{T,\beta '} \!:=\! \bigg \{h : \Big |\big (h/h_{T,\beta '}\big )^{\widetilde{\beta '}-d/2}\!-\!1\Big |\!\le \! \overline{\delta }_T\bigg \}\). Note that there exists a positive constant \(c_0\) such that
Denote the kernel estimator of \((b^j\rho _{b})(x_0)\) with deterministic bandwidth \(h \in {\mathcal {H}}_{T,\beta '}\) by
and set \(g_{T,\beta '}(x_0) := g_{T,\beta '}\big (x_0,h_{T,\beta '}\big )\). Define
and let \(d_T(\beta ):= \sqrt{(d\log T)/\beta }\) such that \(\mathrm{s }_T(\beta ) d_T(\beta ) = \eta _{T,\beta }\). For \(\beta ' \le \beta \), introduce the auxiliary sequence
Lemma 5
(Bound on the bias) Consider the estimator \(g_{T,\beta '}(x_0,h)\) defined in (8.11), and let
For any \({\mathcal {H}}_{T,\beta '} \ni h >0\),
Furthermore,
Proof
The bound on the bias in (8.12) is proven by standard arguments and relies in particular on exploiting the scaling properties of the Fourier transform of \(K_{\beta ',h}\). The remaining assertions are Lemma 1(ii), (iii) in Klemelä and Tsybakov [11].\(\square \)
The principal importance of exponential bounds on the stochastic error of estimators considered in the adaptive procedure was already indicated in the introduction. The Bernstein-type deviation inequality (BI) and its implication (BI+), the basic uniform exponential inequality stated in Lemma 2, can be applied to derive more specific bounds on the stochastic error of the estimators \(g_{T,\beta }\) defined according to (8.11). The following function classes are defined analogously to Butucea [3],
For \(h \in H_{T,\beta }\), let
Lemma 6
Grant Assumptions (BI) and (SG+). For any \(\beta ' > d/2\), the stochastic error \(Z_{T,\beta '}(\cdot )\) defined according to (8.13) has the following properties:
-
(a)
For any \(u \in \big [\tau _T(\beta '), \ R_1 \mathrm{s }_T(\beta ')\sqrt{\log T}\big ]\), \(R_1>0\) an absolute constant, there exist some sufficiently small \(\gamma >0\), independent of \(\beta '\), and some universal constant \(c^{\prime }_1>0\) such that
$$\begin{aligned} \mathbf {P}_b\Bigg (\sup _{h \in H_{T,\beta '}}\big |Z_{T,\beta '}(h)\big | > u\Bigg ) \le c^{\prime }_1 \exp \left( -\frac{1}{2} \bigg (\frac{u(1-\gamma )}{\mathrm{s }_T(\beta ')}\bigg )^2\right) + o\big (T^{-1}\big ).\qquad \quad \end{aligned}$$(8.14) -
(b)
For any \(u\in \big [R_1 \mathrm{s }_T(\beta ')\sqrt{\log T}, \ R_2\big ]\), \(R_1, R_2 >0\) absolute constants, it holds, for some absolute constants \(c^{\prime }_2, c^{\prime }_3 >0\),
$$\begin{aligned} \mathbf {P}_b\Bigg (\sup _{h \in H_{T,\beta '}}\big |Z_{T,\beta '}(h)\big |> u\Bigg ) \le c^{\prime }_2\exp \left( -c^{\prime }_3\bigg (\frac{u}{\mathrm{s }_T(\beta ')}\bigg )^2\right) . \end{aligned}$$ -
(c)
Assume that \(\beta ' < \beta \). Then, uniformly in \(\beta \in {\mathcal {B}}_T\),
$$\begin{aligned}&\sup _{\mathop {\beta '<\beta }\limits ^{\beta '\in \mathcal {B},}} m \sup _{b\in \widetilde{\varPi }(c_1,c_2)} \sup _{\rho _b \in \varSigma _T(\beta ,L)}\psi _{\beta ,L}^{-2}\, \\&\quad \times \,\mathbf {E}_b\left[ \bigg (\sup _{h \in H_{T,\beta '}} \big |Z_{T,\beta '}(h)\big |\bigg )^2 \, {1\!\!1}\bigg \{\sup _{h\in H_{T,\beta '}}\big |Z_{T,\beta '}(h)\big | > \tau _T(\beta ')\bigg \}\right] \rightarrow 0,\\&\sup _{\mathop {\beta '<\beta }\limits ^{\beta '\in \mathcal {B},}} m\sup _{b\in \widetilde{\varPi }(c_1,c_2)} \sup _{\rho _b \in \varSigma _T(\beta ,L)}\psi _{\beta ,L}^{-2}\, \\&\quad \times \, \mathbf {E}_b\left[ \bigg (\sup _{h \in H_{T,\beta '}} \big |Z_{T,\beta '}(h)\big |\bigg )^2 \ {1\!\!1}\bigg \{\sup _{h\in H_{T,\beta '}}\big |Z_{T,\beta '}(h)\big | > \sqrt{\mathrm{s }_T(\beta ')\psi _{\beta ,L}}\bigg \}\right] \rightarrow 0. \end{aligned}$$
Proof
The assertions are analogue to the statements in Lemma 4.3, Lemma 4.5 and Theorem 4.6 in Butucea [3]. For deriving the inequality (8.14) with the specific factor \(1/2\) in the exponent in the current diffusion framework, we however have to go into greater detail. Throughout the proof, \(D_1, D_2, \ldots \) denote positive constants. For fixed \(\delta ' \in (0,1)\) and arbitrary \(u,T>0\), write
for
and, denoting \(M_t(K) := \int _0^t K(X_u)\sum _{r=1}^d \sigma _{jr}\mathrm {d}W_u^r\), \(t>0\),
For any \(u \le R_1 \mathrm{s }_T(\beta ')\sqrt{\log T}\), we have
such that, since \(\beta '>d/2\),
Furthermore, the enhanced spectral gap assumption (SG+) gives
Thus, for \(T\) sufficiently large, \(C_B\Big (\varsigma _b\big (K_{\beta ,{h_{T,\beta '}}}\big )+ \delta ' u\ \big \Vert K_{\beta ,h_{T,\beta '}}\big \Vert _\infty \Big ) \le \mathrm{s }_T^2(\beta ') T.\) The Bernstein-type deviation inequality (BI) therefore implies that
For bounding \(\mathsf {t}_2\) from above, we first use Bernstein’s inequality for continuous martingales which gives, for any \(h>0\),
By means of (BI) and using again that \(\beta '>d/2\), it can be shown that
Adding the upper bounds (8.15), (8.16) and (8.17), we obtain, for some small \(\gamma >0\),
Consider the sequence \(\delta _{T1} := \beta _T\overline{\delta }_T\sqrt{\log T} = (\log \log T)^\delta (\log T)^{-1/2} \rightarrow 0\), and note that, for any \(u>0\),
Since \(u(1-\delta _{T1}) \le u \le R_1 \mathrm{s }_T(\beta ')\sqrt{\log T}\), (8.18) gives an upper bound on the latter summand. For \(T\) large enough, it further holds
Taking into account that
and since
the uniform exponential inequality (BI+) implies that
Summing the upper bounds due to (8.18) and (8.19), we obtain (8.14).
The inequality stated in \(\mathrm{(b) }\) follows as an application of (BI+) with \(K := h_{T,\beta '}^{-d} K_{\max }\) and
Finally, part \(\mathrm{(c) }\) is proven similarly to Theorem 4.6 in Butucea [3] by noting that there exists some positive constant \(R\) such that \(\sup _{h \in H_{T,\beta '}}\big |Z_{T,\beta '}(h)\big | \le R h_{T,\beta '}^{-d}\). A suitable decomposition of
and uniform exponential bounds on the corresponding integrands as they follow from parts \(\mathrm{(a) }\) and \(\mathrm{(b) }\) of this lemma then yield the assertions. \(\square \)
The next lemma contains a decomposition of the normalizing factor \(\psi _{\beta ,L}\) and some relations which are needed later in the proof. For \(h_{T,\beta }\) defined according to (8.10), denote
Lemma 7
Let \(\beta \in [d/2,\infty )\), \(L\in \left[ L_*,L^*\right] \), and denote \(\nu = (\beta ,L)\). It then holds
Furthermore, there exist positive constants \(D_1, \ldots , D_5\), depending only on \(\beta _*, L_*, L^*, d\) and \(\sigma \), such that
and, for \(\beta ' \in [d/2,\infty )\), \(\beta ' < \beta \),
and
Proof
The proof of the decomposition is comparable to the derivation of relation (68) on p. 461 in Klemelä and Tsybakov [11]; for details, see the proof of Lemma 2.6.6 in Strauch [21]. Assertions (8.22) and (8.23) follow analogously to the proof of the relations (44)–(46) in Lemma 4 in Klemelä and Tsybakov [11] (pp. 453–454). For the proof of (8.24), we refer to the proof of Lemma 3.5 in Butucea [3]. \(\square \)
Main part of the proof of the upper bound. Define \(\beta ^-=\beta ^-(\beta )\) by
where \(\beta _T^+ := (\log \log T)^{\delta '}\), for some \(\delta ' \in (\delta ,1)\). We follow the standard approach and decompose the risk successively. Assume that \(b\in \widetilde{\varPi }(c_1,c_2,\sigma )\), let \(\nu = (\beta ,L)\), and set
For ease of notation, we usually suppress the dependence of the risk on the coordinate \(j\).
(I) We first consider the case \(\widehat{\beta }_T^j \ge \beta ^-\), and we show that
Define \(\overline{\beta }= \overline{\beta }(\beta )\) via the equation \(\left( \frac{\log T}{L^2 T}\right) ^{1/(2\beta )} = \left( \frac{\log T}{T}\right) ^{1/(2\overline{\beta })}\). Let \(\beta ^+ \in \mathcal {G}\) be the largest grid point \(\le \overline{\beta }\), and assume that \(T\) is large enough for ensuring \(\beta ^- < \beta ^+\). Denote \(\mathcal {G}_1 = \mathcal {G}_1(\beta ) := \left\{ \beta ' \in \mathcal {G}\mid \beta ^-\le \beta ' \le \beta ^+\right\} \), \(\mathcal {G}_2 = \mathcal {G}_2(\beta ):=\left\{ \beta '\in \mathcal {G}\mid \beta ^+ < \beta ' \le \beta _T\right\} \), and rewrite
Let \(\beta ' \in \mathcal {G}_1 = \mathcal {G}_1(\beta )\) and \(\rho _b\in \varSigma _T(\beta ,L)\), and assume that \(T\) is so large that \(\widetilde{\beta }(\beta ,\beta ')=\beta \). Using Lemma 5, the facts that \(\mathcal {H}_{T,\beta '}\subset H_{T,\beta '}\), that \(\beta '\le \overline{\beta }\) and the definition of \(\overline{\beta }\), it can be shown that
where
The following arguments are along the lines of the proof of the upper bound in Klemelä and Tsybakov [11] (see pp. 461–463). For any \(\beta ' \in \mathcal {G}_1\), there exists some positive constant \(C\) such that
Since \(\Lambda (\beta ,\beta ')\) is uniformly continuous in \(\beta ,\beta ' \in [\beta _*,\infty )\), this implies that \(\Lambda (\beta ,\beta ') \le 1 +\gamma _{T1}\). Furthermore, for any \(\beta ' \in \mathcal {G}_1\), \(\beta \in \left[ \beta _*,\beta _T\right] \), it holds \(\mathrm {b}_{\beta ,\beta '}\le \mathrm {b}_{\beta ,\beta }\ (1+\gamma _{T2})\). Consequently, for any \(\beta ' \in \mathcal {G}_1\), \(\rho _b\in \Sigma _T(\beta ,L)\),
Similar arguments (also see the derivation of line (54) on p. 1591 in Klemelä and Tsybakov [10]) yield
Recall the definition of the stochastic error \(Z_{T,\beta }(\cdot )\). Whenever \(\widehat{\beta }_T^j = \beta ' \in \mathcal {G}_1\) and the event \(A_{T,\beta '}\) holds, the above arguments imply that
The last line holds true since \(\mathcal {H}_{T,\beta '} \subset H_{T,\beta '}\) and in view of the decomposition of the normalizing factor \(\psi _\nu \) according to (8.21). If \(\widehat{\beta }_T^j \ge \beta ^+\), the definition of the estimator \(\widehat{\beta }_T^j\) according to (4.10) implies that \(\big | \widehat{g}_{T,\widehat{\beta }_T^j}^j(x_0) - \widehat{g}_{T,\beta ^+}^j(x_0)\big | \le \widehat{\eta }_{T,\beta ^+}\).
Therefore, if \(\widehat{\beta }_T^j = \beta ' \in \mathcal {G}_2\), it holds on \(A_{T,\beta ^+}\),
In view of the decomposition (8.21), this last line implies that
Thus, using (8.29) and (8.30),
The terms \(\mathsf {p}_1(\cdot ), \ldots , \mathsf {p}_4(\cdot )\) are now considered separately. Note first that, for any \(\beta ' \in \mathcal {G}_1\),
Since (8.26) holds for any \(\beta ' \in \mathcal {G}_1\), it can be shown by means of (8.22) and (8.23) that
The summand in (8.31) is bounded from above by the sum of the terms
and
Part (c) of Lemma 6 entails that the latter term tends to zero, uniformly in \(\beta ' \in \mathcal {G}_1\). Therefore,
Recall that the cardinality \(m\) of the grid \(\mathcal {G}\) satisfies
By construction, \(\beta ^+ \in \mathcal {G}_1\), such that \(\mathsf {p}_3(\beta ')\) is upper-bounded analogously. Consequently,
For \(\mathsf {p}_2(\cdot )\) and any \(\beta ' \in \mathcal {G}_1\), there exists some universal constant \(c_0\) such that
The regularity conditions on the bandwidth and the kernel used for defining \(\widehat{\rho }_T(x_0)\) ensure that, for any \(\beta ' \in (d/2,\beta ]\) and some sufficiently small constant \(\alpha >0\) fixed,
This implies that \(\mathsf {p}_2(\beta ')\) is exponentially small, for any \(\beta ' \in \mathcal {G}_1\), such that \(\sum _{\beta ' \in \mathcal {G}_1}\mathsf {p}_2(\beta ') \rightarrow 0.\) Analogously, it follows that \(\sum _{\beta ' \in \mathcal {G}_2}\mathsf {p}_4(\beta ') \rightarrow 0\), completing finally the verification of (8.25).
(II) It is proven now that
Let \(\beta ' \in \mathcal {G}_T\), and assume that the event \(A_{T,\beta '}\) holds. In view of the definition of the stochastic error \(Z_{T,\beta '}\) in (8.13) and taking into account Lemma 5, it holds, whenever \(\rho _b\in \varSigma _T(\beta ,L)\),
Then, using the definition of \(\mathrm {b}_{T,\beta '}\) in (8.20),
The term \(g_1(\nu )\) is bounded from above by exploiting the fact that the probability to underestimate the value of \(\beta \) by \(\widehat{\beta }_T^j\) substantially is small, whenever \(\rho _b\in \Sigma _T(\beta ,L)\). Recall that \(m\) is the cardinality of the grid \(\mathcal {G}\).
Lemma 8
(Probability of undershooting) Let \(\beta \in [\beta _*,\infty )\), \(\beta ' \in \mathcal {G}\), \(\beta ' < \beta ^-\), \(L\in \left[ L_*,L^*\right] \), and \(\nu = (\beta ,L)\). Then there exists some constant \(K\), depending only on \(\beta _*,L_*,L^*,d\) and \(\sigma \) such that, for any \(b\in \widetilde{\varPi }(c_1,c_2,\sigma )\),
Proof
The proof substantially relies on applications of Lemma 2. Since the basic arguments are similar to those used in the proof of Lemma 4.8 in Butucea [3] and the proof of Lemma 5 in Klemelä and Tsybakov [11], we do not include the proof but refer to Strauch [21]. \(\square \)
Let \(\beta \in \left[ \beta _*,\beta _T\right] \), \(\beta ' \in \mathcal {G}\), \(L \in \left[ L_*,L^*\right] \), \(\nu = (\beta ,L)\). By means of Lemma 8 and using relation (8.24) in Lemma 7, we obtain
In view of the upper bound on the cardinality \(m\) of the grid \(\mathcal {G}= \mathcal {G}_T\) in (8.32), it follows that \(\lim _{T\rightarrow \infty }\sup _{\nu \in \mathcal {B}_T}g_1(\nu ) = 0,\) and the first assertion in Lemma 6(c) immediately gives \(\lim _{T\rightarrow \infty }\sup _{\nu \in \mathcal {B}_T}g_2(\nu ) = 0\). Note finally that, for any \(\beta ' \in \mathcal {G}\),
Consequently, taking into account (8.33), it holds, independent both of \(\beta \) and \(\beta '\),
thus completing the proof of (8.34). \(\square \)
Rights and permissions
About this article
Cite this article
Strauch, C. Exact adaptive pointwise drift estimation for multidimensional ergodic diffusions. Probab. Theory Relat. Fields 164, 361–400 (2016). https://doi.org/10.1007/s00440-014-0614-4
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00440-014-0614-4
Keywords
- Ergodic diffusion
- Minimax drift estimation
- Exact constants in nonparametric smoothing
- Sharp adaptivity
- Pointwise risk