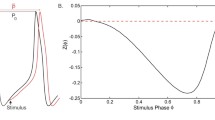
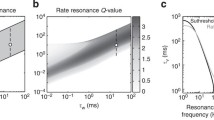
Abstract
We study multifrequency Hebbian plasticity by analyzing phenomenological models of weakly connected neural networks. We start with an analysis of a model for single-frequency networks previously shown to learn and memorize phase differences between component oscillators. We then study a model for gradient frequency neural networks (GrFNNs) which extends the single-frequency model by introducing frequency detuning and nonlinear coupling terms for multifrequency interactions. Our analysis focuses on models of two coupled oscillators and examines the dynamics of steady-state behaviors in multiple parameter regimes available to the models. We find that the model for two distinct frequencies shares essential dynamical properties with the single-frequency model and that Hebbian learning results in stronger connections for simple frequency ratios than for complex ratios. We then compare the analysis of the two-frequency model with numerical simulations of the GrFNN model and show that Hebbian plasticity in the latter is locally dominated by a nonlinear resonance captured by the two-frequency model.











Similar content being viewed by others
Notes
The amount of change in connection phases \(\theta _{ij}\) after a perturbation depends on connection amplitudes \(A_{ij}\). Once the connections grow strong enough compared to the magnitude of perturbation, and when learning is slow (with small \(\gamma \) and \(\kappa \)), the plastic connections act like fixed coupling and are not altered significantly by sporadic perturbations of small amplitudes. Accordingly, the oscillators are attracted back to the previous relative phase after a small perturbation. Thus, plastic connections which are neutrally stable on a long timescale constitute an attractor on a short timescale. For the purpose of demonstrating neutral stability, the simulation shown in Fig. 2 used fast learning and a strong perturbation.
We chose the quintic coefficient to be \(-1\) because here we want to examine the stabilization of amplitude dynamics without altering phase dynamics. In fully expanded models (13) and (24), the quintic coefficient \(d_i = \beta _{2i}+\text {i}\delta _{2i}\) has both amplitude (radial) and phase (azimuthal) components.
Note that the oscillation frequency of plastic connection \({\dot{\theta }}_{ij} = -\frac{\kappa r_i r_j}{A_{ij}} \sin \psi _{ij}\) is proportional to \(\kappa \). When learning is slow (with small \(\gamma \) and \(\kappa \)), plastic connections oscillate at slow frequencies and behave like fixed coupling on a short timescale. See footnote 2 for a related discussion on the timescale of learning.
See Eq. (9), for example, where the intrinsic part of the learning equation takes a similar form as the oscillator equation, except the former does not have any imaginary terms like \(\text {i}\omega \), which can be interpreted as the natural frequency being zero. Thus, plastic connections resonate when the oscillators maintain a fixed phase difference (or phase-locked) because that is when the input term \(\kappa z_i {\bar{z}}_j\) is stationary.
Note that (13) has \(\epsilon \) in the intrinsic higher-order terms (with the coefficient \(d_i\)) as well as in the coupling terms (with \(c_{ij}\)). The original weakly connected system is considered \(\epsilon \)-perturbation of the uncoupled system, from which the canonical model is derived using averaging theory (Hoppensteadt and Izhikevich 1996a). Here, to capture resonance between distinct frequencies, the canonical model is expanded to include higher-order perturbation terms (see Hoppensteadt and Izhikevich 1997, p. 172). Hence, both the higher-order intrinsic terms and the coupling terms are expressed as powers of \(\epsilon \).
References
Andronov AA, Leontovich EA, Gordon IE, Maier AG (1971) The theory of bifurcations of dynamical systems on a plane. Israel Program of Scientific Translations, Jerusalem
Aoki T, Aoyagi T (2011) Self-organized network of phase oscillators coupled by activity-dependent interactions. Phys Rev E 84(6):066109. https://doi.org/10.1103/PhysRevE.84.066109
Aoyagi T (1995) Network of neural oscillators for retrieving phase information. Phys Rev Lett 74(20):4075–4078. https://doi.org/10.1103/PhysRevLett.74.4075
Arnold VI (1978) Ordinary differential equations. MIT, Cambridge, Mass., oCLC: 833071813
Arnold VI (1988) Geometrical methods in the theory of ordinary differential equations, Grundlehren der mathematischen Wissenschaften, vol 250. Springer, New York. https://doi.org/10.1007/978-1-4612-1037-5
Assenza S, Gutiérrez R, Gómez-Gardeñes J, Latora V, Boccaletti S (2011) Emergence of structural patterns out of synchronization in networks with competitive interactions. Sci Rep 1(1):99. https://doi.org/10.1038/srep00099
Bregman AS (1990) Auditory scene analysis: the perceptual organization of sound. MIT Press, Cambridge
Caporale N, Dan Y (2008) Spike timing–dependent plasticity: a Hebbian learning rule. Annu Rev Neurosci 31(1):25–46. https://doi.org/10.1146/annurev.neuro.31.060407.125639
Gerstner W, Kistler WM (2002) Mathematical formulations of Hebbian learning. Biol Cybern 87(5–6):404–415. https://doi.org/10.1007/s00422-002-0353-y
Guckenheimer J, Holmes P (1983) Nonlinear oscillations, dynamical systems, and bifurcations of vector fields. No. 42 in Applied Mathematical Sciences. Springer, New York
Hebb DO (1949) The organization of behavior: a neuropsychological theory. Wiley, New York
Hoppensteadt FC, Izhikevich EM (1996a) Synaptic organizations and dynamical properties of weakly connected neural oscillators. I. Analysis of a canonical model. Biol Cybernet 75:117–127. https://doi.org/10.1007/s004220050279
Hoppensteadt FC, Izhikevich EM (1996b) Synaptic organizations and dynamical properties of weakly connected neural oscillators. II. Learning phase information. Biol Cybernet 75:129–135. https://doi.org/10.1007/s004220050280
Hoppensteadt FC, Izhikevich EM (1997) Weakly connected neural networks. No. 126 in Applied Mathematical Sciences. Springer, New York
Hoppensteadt FC, Izhikevich EM (2000) Pattern recognition via synchronization in phase-locked loop neural networks. IEEE Trans Neural Netw 11(3):734–738. https://doi.org/10.1109/72.846744
Hoppensteadt FC, Izhikevich EM (2001) Canonical neural models. In: Arbib MA (ed) The handbook of brain theory and neural networks, 2nd edn. MIT Press, Cambridge, pp 181–186
Humphries C, Liebenthal E, Binder JR (2010) Tonotopic organization of human auditory cortex. NeuroImage 50(3):1202–1211. https://doi.org/10.1016/j.neuroimage.2010.01.046
Hyafil A, Giraud AL, Fontolan L, Gutkin B (2015) Neural cross-frequency coupling: connecting architectures, mechanisms, and functions. Trends Neurosci 38(11):725–740. https://doi.org/10.1016/j.tins.2015.09.001
Kasatkin DV, Yanchuk S, Schöll E, Nekorkin VI (2017) Self-organized emergence of multilayer structure and chimera states in dynamical networks with adaptive couplings. Phys Rev E 96(6):062211. https://doi.org/10.1103/PhysRevE.96.062211
Kim JC (2017) A dynamical model of pitch memory provides an improved basis for implied harmony estimation. Front Psychol 8:666. https://doi.org/10.3389/fpsyg.2017.00666
Kim JC, Large EW (2015) Signal processing in periodically forced gradient frequency neural networks. Front Comput Neurosci 9:152. https://doi.org/10.3389/fncom.2015.00152
Kim JC, Large EW (2019) Mode locking in periodically forced gradient frequency neural networks. Phys Rev E 99(2):022421. https://doi.org/10.1103/PhysRevE.99.022421
Kuznetsov YA (2004) Elements of applied bifurcation theory. Applied Mathematical Sciences, vol 112. Springer, New York. https://doi.org/10.1007/978-1-4757-3978-7
Large EW (2010) Neurodynamics of music. In: Jones MR, Fay RR, Popper AN (eds) Music perception. Springer, New York, pp 201–231
Large EW (2011) Musical tonality, neural resonance and Hebbian learning. In: Agon C, Andreatta M, Assayag G, Amiot E, Bresson J, Mandereau J (eds) Mathematics and Computation in Music, no. 6726 in Lecture Notes in Artificial Intelligence. Springer, Berlin, pp 115–125
Large EW, Almonte FV, Velasco MJ (2010) A canonical model for gradient frequency neural networks. Physica D 239:905–911. https://doi.org/10.1016/j.physd.2009.11.015
Large EW, Herrera JA, Velasco MJ (2015) Neural networks for beat perception in musical rhythm. Front Syst Neurosci 9:159. https://doi.org/10.3389/fnsys.2015.00159
Large EW, Kim JC, Flaig NK, Bharucha JJ, Krumhansl CL (2016) A neurodynamic account of musical tonality. Music Percept 33(3):319–331. https://doi.org/10.1525/mp.2016.33.3.319
Lerud KD, Almonte FV, Kim JC, Large EW (2014) Mode-locking neurodynamics predict human auditory brainstem responses to musical intervals. Hear Res 308:41–49. https://doi.org/10.1016/j.heares.2013.09.010
Lerud KD, Kim JC, Almonte FV, Carney LH, Large EW (2019) A canonical oscillator model of cochlear dynamics. Hear Res 380:100–107. https://doi.org/10.1016/j.heares.2019.06.001
Maslennikov OV, Nekorkin VI (2015) Evolving dynamical networks with transient cluster activity. Commun Nonlinear Sci Numer Simul 23(1–3):10–16. https://doi.org/10.1016/j.cnsns.2014.11.019
Maslennikov OV, Nekorkin VI (2017) Adaptive dynamical networks. Phys Usp 60(7):694–704. https://doi.org/10.3367/UFNe.2016.10.037902
Maslennikov OV, Nekorkin VI (2018) Hierarchical transitions in multiplex adaptive networks of oscillatory units. Chaos Interdiscipl J Nonlinear Sci 12:121101. https://doi.org/10.1063/1.5077075
Murdock J (2003) Normal forms and unfoldings for local dynamical systems. Springer monographs in mathematics. Springer, New York
Park SW, Dijkstra TMH, Sternad D (2013) Learning to never forget-time scales and specificity of long-term memory of a motor skill. Front Comput Neurosci 7:111. https://doi.org/10.3389/fncom.2013.00111
Shouval H (2007) Models of synaptic plasticity. Scholarpedia 2(7):1605. https://doi.org/10.4249/scholarpedia.1605
Strogatz SH (1994) Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. Perseus Books, Cambridge
Stuart JT (1958) On the non-linear mechanics of hydrodynamic stability. J Fluid Mech 4(1):1–21. https://doi.org/10.1017/S0022112058000276
Tichko P, Large EW (2019) Modeling infants’ perceptual narrowing to musical rhythms: neural oscillation and Hebbian plasticity. Ann N Y Acad Sci 1453(1):125–139. https://doi.org/10.1111/nyas.14050
Wilson HR, Cowan JD (1972) Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J 12:1–24. https://doi.org/10.1016/S0006-3495(72)86068-5
Zanone PG, Kelso JAS (1992) Evolution of behavioral attractors with learning: Nonequilibrium phase transitions. J Exp Psychol Hum Percept Perform 18(2):403–421. https://doi.org/10.1037/0096-1523.18.2.403
Acknowledgements
The authors thank Parker Tichko, Karl Lerud, and two anonymous reviewers for their helpful comments on the previous versions of the paper.
Funding
Early stages of this work were supported by National Science Foundation BCS-1027761 and Air Force Office of Scientific Research FA9550-12-10388.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by Benjamin Lindner.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Kim, J.C., Large, E.W. Multifrequency Hebbian plasticity in coupled neural oscillators. Biol Cybern 115, 43–57 (2021). https://doi.org/10.1007/s00422-020-00854-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00422-020-00854-6